一种新的电压偏差预测方法

王知芳, 杨 秀， 潘爱强

(1. 上海电力学院电气工程学院，上海 200090；2. 国网上海市电力公司电力科学研究院，上海 200437)

0 引言

随着非线性负荷和电力电子设备的大量使用，电能质量问题日益严重，受到了社会各界的广泛关注。深入挖掘电能质量监测数据，对电能质量的变化趋势做出预测和预警，成为保证电力安全、稳定、经济输送的必要措施[1]。

电能质量问题分为稳态和暂态电能质量问题。稳态电能质量问题包括电压偏差、频率偏差、电压波动与闪变、谐波及三相不平衡度[2]。其中电压偏差的危害最为明显，电压过高造成设备过电压，威胁绝缘，减少使用寿命；电压过低使用户设备不能正常使用。因此，预测电压偏差变化趋势并采取一定措施对于电力系统的安全稳定运行具有很高的应用价值。且不同的电能质量指标数据具有不同的特征，若用一个预测模型来预测5项稳态指标，会造成精度差的问题，因此文中对电压偏差指标建立预测模型。

常用的预测方法有时间序列法、灰色预测法、支持向量机预测法等。但时间序列法注重数据的拟合，对影响电能质量的不确定性因素考虑不足；灰色预测法对数据的离散程度有要求，当数据离散程度较大时，预测精度较差；支持向量机在处理随机波动性较强的数据时，精度较差，且数据集规模过大时，训练时间长，速度慢[3]。

目前，对电能质量预测的研究文献较少，而负荷预测方法已比较成熟，可参考负荷预测的方法来进行电能质量预测。文献[4—6]采用基于小波分析的预测方法，将负荷数据进行分解，能够改善预测精度，但预测精度过多依赖于历史相似日的选取，预测结果不稳定。文献[7—8]采用基于决策树的负荷预测模型，模式简单，易于理解，但在选取属性进行扩展时，对各属性间的相关性考虑较少，且对噪音敏感；文献[9—11]采用综合预测方法，结合多种预测模型的有效信息，优势互补，改善预测精度，但是模型的权重确定困难，建模难度大；文献[12—14]采用偏最小二乘回归分析法进行负荷预测，通过对成分的提取，最大限度地利用了数据信息，但如何提高成分解释能力仍然难度较大。

电能质量预测的方法尚不成熟，研究文献极少。文献[15]提出一种基于Monte Carlo抽样的电铁电能质量预测方法，即先用Monte Carlo抽样方法对牵引负荷进行随机波动处理，再对负序、谐波等指标进行预测，但是此方法预测对象有限制，适用性差，仅适用于具有单相独立性、随机波动性的电铁一类的电能质量预测；文献[16]先利用ARIMA时间序列算法对有功功率进行预测，又根据有功功率与电能质量稳态指标的相关性建立反向传播(back propagation ,BP)神经网络预测模型，但是此方法是间接预测方法，有功功率的预测结果较大程度影响最终电能质量的预测结果；文献[17]采用神经网络的预测模型对变电站和重点负荷用户、风电、光伏等用户电能质量进行短期预测，但是此预测方法过于单一，且对预测精度没有做具体分析和说明。

文中针对电压偏差非线性、周期性的特点并结合实时气象数据提出一种基于聚类算法和BP神经网络的电压偏差预测方法，首先选择与待预测点相似相近的历史数据；然后采用聚类算法对气象因素聚类，根据聚类结果提取与待预测点同类的历史数据；最后选择BP神经网络建立电压偏差预测模型。将本方法应用到上海市某电站电压偏差数据，证明了文中提出的预测方法精度更高。

1 算法描述

针对传统K-means聚类的不足，文中引进亲和力传播(affinity propagation，AP)聚类算法，对经过主成分分析法(principal component analysis, PCA)降维处理之后的气象数据主成分进行聚类，根据聚类结果提取与待预测点同类的历史数据，最后选择BP神经网络建立电压偏差预测模型。

1.1 PCA降维

由于气象因素较多，在应用BP神经网络进行电压偏差预测时，若直接将这些因素作为输入，会导致BP神经网络学习速度慢，效率低，而且无关变量的引入会导致预测精度下降甚至不能完成学习，因此有必要对气象数据进行降维处理。

PCA是一种数学降维算法，将原来众多具有相关性的变量，重新组合成一组新的相互无关的综合变量来代替原来变量[18]，这些综合变量即为主成分。

V=eigvec[cov(X)]

(1)

式中：X为归一化的数据矩阵；cov(X)为协方差矩阵；V的列向量为cov(X)的正交单位特征向量。

将X降至L维后的数据矩阵为：

P=XVL

(2)

式中：VL为矩阵V的前L列。

1.2 AP聚类分析

AP聚类是Frey和Dueck 于2007年在Science杂志上提出的一种新的无监督聚类算法[19-20]。AP聚类过程是信息传递的过程，利用吸引信息矩阵R和归属信息矩阵A在数据点之间交换信息，不断迭代更新2个信息矩阵，直到迭代结束。r(i,k)与a(i,k) 分别为i点与k点之间的吸引信息矩阵元素和归属信息矩阵元素，其值越强,则k点作为聚类中心的可能性就越大,并且i点隶属于以k点为聚类中心的类簇的可能性也越大。r(i,k)与a(i,k)计算公式如下：

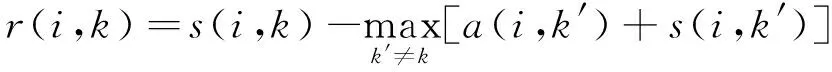
(3)

(4)

由于AP聚类算法迭代过程容易产生震荡，所以每次迭代都加上一个阻尼系数λ,λ∈(0,1)。

(5)

式中：s(i,k)为i点与k点之间的相似度。

相对于传统聚类，AP聚类算法有如下优点：

(1) 不需要事先指定聚类个数K；

(2) 多次执行得到的结果完全一样，不需要随机选取初值；

(3) 比其他单一聚类法的误差平方和都要低；

(4) 通过输入相似度矩阵来启动算法，因此对距离矩阵的对称性没要求，数据适用范围大。

AP算法的流程如图1所示。

图1 AP算法流程Fig.1 Flowchart of APalgorithm

1.3 BP神经网络

针对电压偏差非线性、周期性的特点，文中选取神经网络算法建立预测模型。神经网络具备很强的学习能力，能更好地适应数据空间的变化和各种复杂的数据关系。

BP神经网络是一种多层前馈神经网络，该网络的主要特点是信号前向传递，误差反向传播。BP神经网络广泛应用于分类识别、逼近、回归、压缩等领域[21-24]，其结构见图2。

图2 BP神经网络结构模型Fig.2 BP neural network structure model

2 案例分析

2.1 电压偏差预测流程

文中选取2012年4月10日至5月15日，2013年4月10日至5月15日，2014年4月1日至4月26日共2352个整时点气象数据和电压偏差数据作为历史数据，对接下来的2014年4月27日、28日整时点的电压偏差进行预测。文中气象数据来自于上海浦东国际机场所使用的天气数据，电压偏差数据来自上海市某变电站的真实数据，组成如下的数据集记录：整点时刻，气温，露点，湿度，气压， 风向，风速，状况，电压偏差。

2.2 改进集成聚类算法

2.2.1 PCA降维处理

由于影响电压偏差预测精度的因素很多，为避免信息冗余现象，需对影响因素进行降维。分析数据集中数据的相关性，绘制相关性强度图，如图3所示。由图可知，气象因素中气温、湿度、风速、露点与电压偏差的相关性较高，但同时气象因素内部间的相关性也较高，若只提取与电压偏差相关性较强的气象因素，则会出现信息重复现象。

图3 相关性强度Fig.3 Correlation strength

所以，将气象数据进行PCA降维处理，得到一组相互独立又信息量大的主成分，根据贡献率，文中将原始气象数据PCA降维为4维。

2.2.2 AP聚类

AP算法的输入为数据点之间的相似度矩阵S，文中数据点i和j的相似度为s(i,j)=-(xi-xj)2。图4为AP聚类迭代过程。

图4 AP聚类迭代过程Fig.4 Iteration of AP clustering

将降维后的气象数据进行AP聚类，由图4可知，AP聚类迭代约10次便趋于稳定。

2.2.3 聚类评价指标SSE

误差平方和(sum of squared errors，SSE)指标ISSE用一个子类到所在类簇的聚类中心的欧氏距离来表示，即：

(7)

传统K-means聚类需事先给定聚类数K值，聚类结果受初始聚类中心的影响大，导致K-means聚类算法不稳定，SSE值为3 724.526 8；AP聚类算法不需要随机选取初值，多次执行AP算法得到的结果相同，稳定性好，SSE值为2 537.064 9，克服了K-means聚类算法的不足,AP聚类算法的误差平方和较小，类簇间的分散性高，类簇内的紧凑性好。

2.3 BP神经网络预测

2.3.1 BP神经网络设计

输入向量为改进集成聚类得到的与待测点的气象因素同类的历史数据集，因此为一个4维向量；输出向量为整点时刻的电压偏差，为1维向量。BP神经网络适合求解内部机制复杂的问题，但是初始权重敏感，文中取10次预测结果的均值作为最终预测结果。

2.3.2 预测结果

文中提出的改进方法，与传统BP神经网络预测方法、BP神经网络结合PCA降维的预测方法程序均在MATLAB平台上成功运行，将其结果进行对比，如图5、图6所示。并计算其平均相对误差：

(8)

图5 预测结果对比Fig.5 Comparison of forecasting results

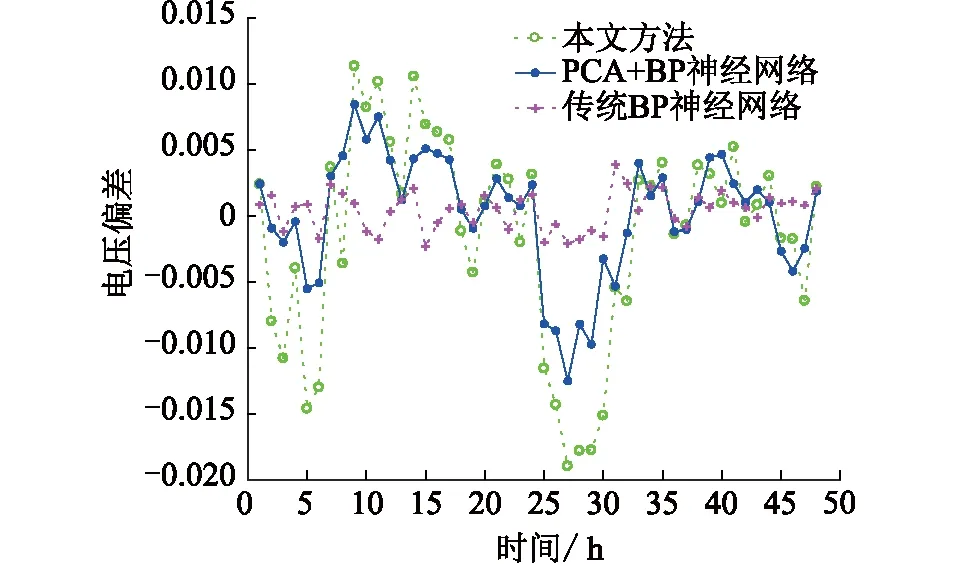
图6 预测误差对比Fig.6 Comparison of forecasting errors

由图5、图6可知，文中改进方法比传统BP神经网络、PCA+BP神经网络预测结果的平均相对误差都低，说明该改进方法中PCA降维和AP聚类2个步骤均能够提高预测精度，这是因为通过PCA降维处理，剔除了无关变量和冗余变量，得到相互独立又信息量大的主成分；而通过AP聚类可以确定历史数据之间的亲疏关系，提取与待测点同类的数据对神经网络进行训练，减少了无关历史数据的影响不良影响，进一步提高了预测精度。将4月27日、4月28日的3种方法预测结果的相对误差落在某一范围内的频数用直方图表示，得到图7—9所示的3种方法的预测误差分布直方图。

图7 传统BP神经网络法误差分布Fig.7 Distribution histogram ofthe traditional BP model

图8 PCA+BP神经网络法误差分布Fig.8 Distribution histogram ofthe BP model with PCA

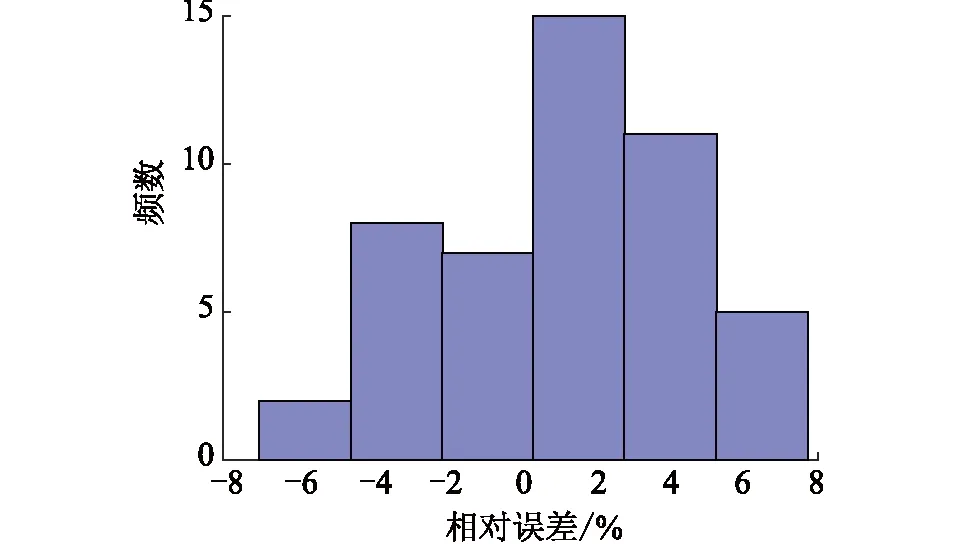
图9 本文改进方法误差分布Fig.9 Distribution histogram ofthe proposed method

从图7—9可以看出文中提出的改进预测方法相对误差在0附近更为集中。最终预测方法误差对比如表1所示，文中方法平均相对误差为3.06%，比传统神经网络降低了10.82%，而且传统神经网络和PCA+BP神经网络的预测结果相对误差控制在3%以内的概率分别为12.5%和25%，而文中改进预测方法预测结果相对误差控制在3%以内的概率达到54.17%，极端相对误差只是小概率事件。综上所述，文中改进预测方法在电压偏差预测中效果更好，为下一步电压偏差预警及电压偏差问题策略制定提供可靠依据。

表1 预测方法误差对比Tab.1 Comparison of forecasting errors %

3 结语

文中针对电压偏差非线性、周期性的特点，同时考虑气象因素，通过将聚类算法与BP神经网络结合，建立电压偏差 预测模型。

(1) 由于影响电压偏差预测精度的因素过多，为避免信息干扰和信息重复，将气象数据进行PCA降维处理，得到一组相互独立又信息量大的主成分，将气象主成分进行聚类处理。

(2) 引入AP聚类算法，克服了传统K-means聚类算法的不足,结果证明AP聚类算法效果更好。

(3) 选择与待预测整时点同类的历史数据集作为训练样本数据集，运用BP神经网络进行训练并预测，将其预测结果与传统BP神经网络、PCA+BP神经网络预测结果相比较，证明了本文提出的方法整体预测指标更好。

虽然文中提出的预测模型能够较好的预测短期电压偏差，但模型仍有提高的空间。如：BP聚类算法样本依赖性强且初始权重为随机给定，导致BP神经网络预测结果稳定性欠佳。因此可基于以上问题，对文中预测模型进一步改进。