叶片组的变参数环板等效建模方法*

姜萌 张美艳 郭其威 唐国安†

(1.复旦大学 航空航天系, 上海 200433) (2.上海宇航系统工程研究所, 上海 201108)

引言

转子的振动特性长期受到学者关注,从最初经典的两端简支、带刚性圆盘弹性转轴的Jeffcott转子[1],到单盘转子[2],再到含多个轮盘的多盘转子[3],研究理论和分析方法不断丰富完善.张文[4]指出,高转速转子中应将叶盘看作弹性体,建立柔盘-柔轴的全弹性转子模型进行处理.但是,如果叶片-轮盘-轴各部件都采用有限元模型描述,那么完整的转子模型自由度将十分庞大,计算中须耗费大量时间,在结构优化等应用中存在困难.因此,对叶片-轮盘这一转子中的基本构件进行模型降阶依然具有重要意义,通过降低单级弹性叶-盘模型的自由度可有效提高整体计算的效率.

有限单元法是一种普遍应用的数值方法,也成为许多商用计算程序分析叶盘动力学特性的基本算法.Hsieh和Abel[5]综合考虑旋转叶-盘的转动非线性,分别利用分布和集中质量方法建立有限元模型.Genta和Tonoli[6]将叶片组的陀螺效应和离心载荷考虑在内,建立叶盘组合体的有限元模型.周传月等[7]将Nastran应用于某型叶盘组合体的固有振动特性分析中.

为缩减模型总自由度、提高计算效率,一些基于有限元模型的简化数值算法也日益成熟.常见的简化算法有三类:利用叶盘回转对称特性的矩阵变换[8,9]、假设模态法[10]和模态综合法[11,12].有学者则根据叶-盘结构的特点,采用等效的少量自由度模型进行建模,提高计算效率.如Kaza和Kielb[13]等将叶片等效为弹性梁模型,Turhan和Bulut[14]建立了以欧拉伯努利梁来代替叶片的理想模型.

在优化设计等应用中,含多级叶盘的转子以及定子、机匣等组件的发动机系统模型的规模庞大,需进一步发展面向多级叶片-轮盘系统的动力学分析的方法.一些学者提出了相应的分析模型和算法[15,16].Pan等[17]建立了叶盘轴结构混合维度的有限元模型,实现三维实体叶片与二维轴对称盘轴的耦合模态分析,能够较大地提高叶轮类结构的分析效率而不失分析精度.本文作者根据周向环绕的单级叶片组的物理参数和模态分析结果,将叶片组等效为固有特性相近的正交异性环形板[18],用轴对称模型表示单级叶盘组合体,从而降低模型的自由度.

本文基于之前的研究,提出了新的正交各向异性轴对称叶盘组合体模型,能表现出组合体轴向弯曲与周向扭转的振动耦合特性.采用的方法是通过多个工况条件下的静力学等效估算正交异性弹性参数的初值,再以固有频率的误差作为目标函数,由极小化过程确定弹性参数的终值.

1 叶片组的各向异性环板等效模型

图1示意的是具体的研究对象,一个带叶冠的叶盘组合体,外围叶冠和中部轮盘均可以作为回转体建模,不需缩聚.周向排列的多条叶片将被等效成正交异性环形板,如图2所示.

图1 研究对象:带冠叶盘组合体模型Fig.1 Object:Bladed disk model with shroud

图2 叶片组等效前后模型Fig.2 Initial and equivalent model of blade group

1.1 环板的厚度函数

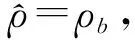
(1)

其中,h0和h1是环板内外缘的待定厚度值.

(2)

其中:

(3)

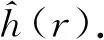
1.2 环板的弹性参数

由于初始带冠叶片在受到轴向力的作用时,不仅会产生轴向位移,同时发生周向扭转.在估算环板弹性参数前,需对其选定一个材料主轴坐标系,使得等效环板在受相同外力作用时,位移的大小和方向能够保持和初始叶片一致.为简便起见,文中采用单一的角度,在总体上模拟出轴向的加载可产生周向位移的情形.

如图3所示,分别将各向异性环板的材料主轴坐标系和总体坐标系记为o1-x1y1z1、o-xyz,其各个子午面上材料的主轴y1总是指向环板的径向,而x1与环板所在平面法线x有一个夹角α.可对初始带冠叶片和等效环板施加相同的外力,通过调节α的大小,保证二者位移效果的一致性,以此确定α和材料主轴坐标系.

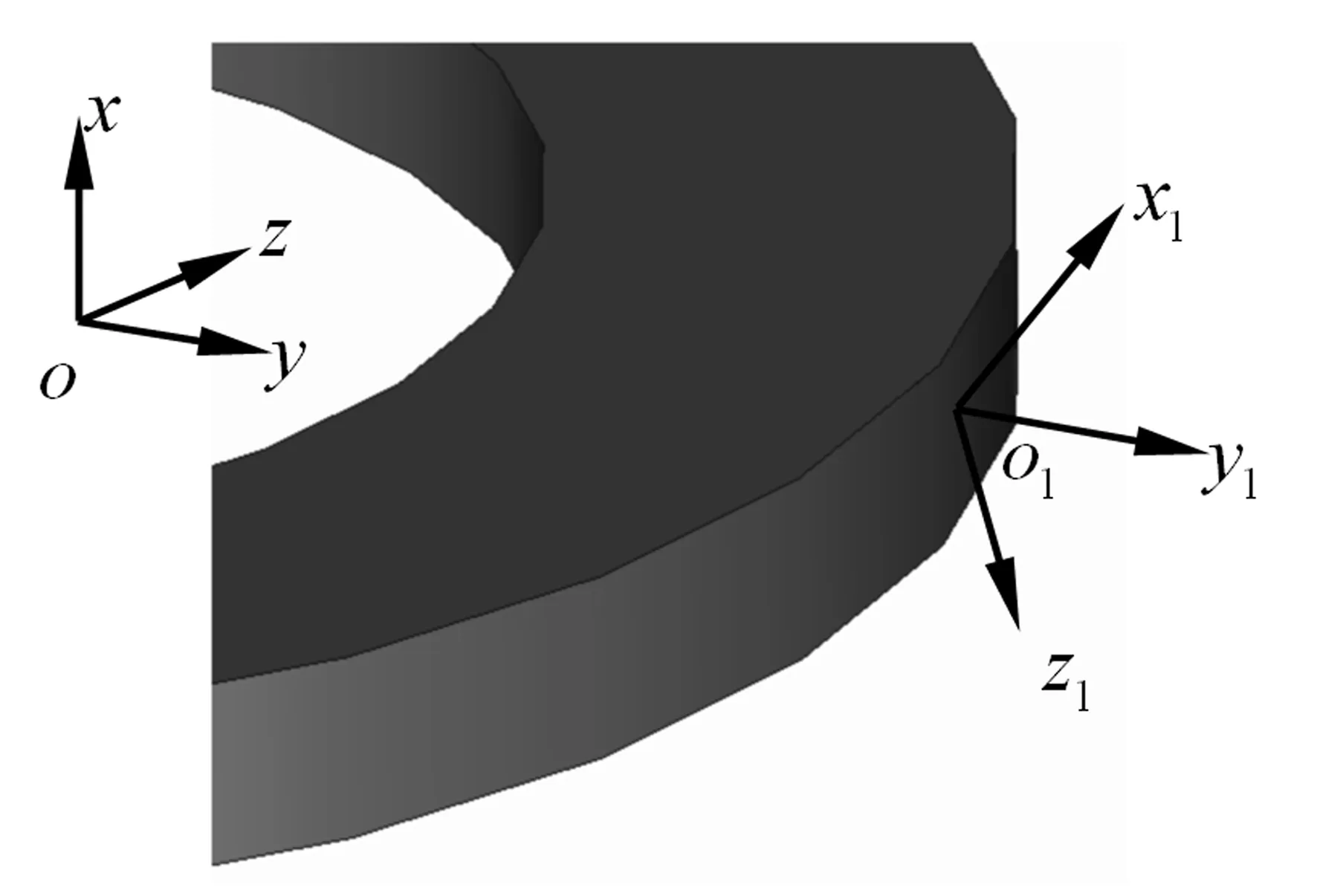
图3 环板材料主轴方向示意图Fig.3 Material principle axis diagram of annular plate

在材料主轴坐标系下,等效环板的正交各向异性本构关系为:

σ=D0ε

(4)

其中,弹性矩阵D0为:

(5)

含有d11,d12,…,d66共9个待定的弹性参数.利用转轴公式[19]可将上述主轴坐标系下的弹性矩阵转换到总体坐标系下:

D=TσD0TσT

(6)

其中,Tσ为应力转换矩阵,与夹角α有关.

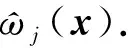
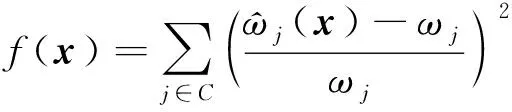
s.t.x∈X

(7)

其中,X为弹性参数的可行域集合,C为振动模态的阶次集合.

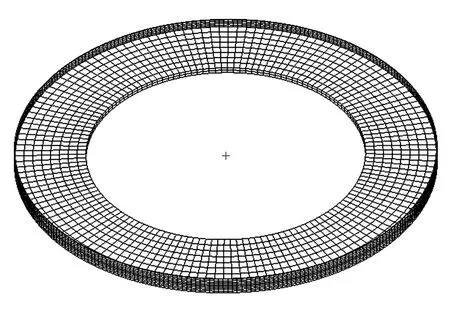
图4 等效带冠弹性环板模型Fig.4 Equivalent elastic annular plate model with shroud

对于非线性规划问题(7),目标函数f(x)是非线性的,可能存在多个局部解,通常需要给出合理的设计变量初值,才能获得有效的极小解.第2节将给出弹性参数初值的估算方法.

2 带叶冠环板的弹性参数估算

模型等效过程示意如图5所示,其中,深灰色实体为等效前的周期重复排列的叶片组,浅灰色实线围成的区域(覆盖叶片组及其间隙的六面体)为等效后的连续弹性板.材料主轴o1-x1y1z1由总体坐标系o-xyz绕y轴旋转α得到.

图5 模型等效过程示意图Fig.5 Diagram of equivalent model

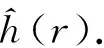
2.1 基本假设

确定弹性参数初值时,不必太精确,仅为给出式(7)中设计变量的合理区间.根据初始叶片组的实际分布和叶片间的传力特征,如叶片沿方向o1z1独立分布,o1z1方向的正应变不能产生该方向的正应力,可假设式(5)弹性矩阵D0中的d33=0,同理,假设d55=d23=d13=0.考虑到d11与三维板的横向振动有关,在后续0、1节径的模态中影响不显著,优化时,可暂将初值假设为:

d11≈d22

(8)

d12是x方向应变与其引起的y方向的应力之比,改变d12的大小,对最终频率的影响亦不显著,优化前可将其初值设为:

(9)

故仅剩三个待定的弹性参数d22、d44和d66,可通过不同工况下的静力学等效估算其初值,静力学等效原则为:等效前后的模型受相同外力,产生相同的变形.算例中通过施加外力fx和外力矩mz,依据上述等效原则可求得初值,等效时基于单条叶片,实现过程基于最小势能原理.

公式推导中,可将回转排列的叶片组近似看作平行排列,那么单条叶片的等效及弹性参数初值的计算公式推导均可在直角坐标系下完成.将等效单条叶片的弹性板沿周向复制若干次即可得到整体的等效环板模型.

2.2 等效环板弹性参数估算公式

假定等效叶片组的三维板,在受到一定外力(包含弯矩、拉力、剪力)作用下的变形位移u是关于未知系数a的线性函数,关系式为:

u=N(x,y,z)a

(10)

其中:

u={u,v,w}T,a={a1,a2,a3}T

N(x,y,z)的形式可根据初始叶片受力后的实际变形设定.根据几何方程,得应变场:

ε=Pa

(11)

利用本构方程可得应力场,由于刚度矩阵中包含待定的弹性参数,故将应力场表达为关于弹性参数的函数形式,如下:

σ(d11,d12,…,d66)=Dε

(12)

积分可得到弹性应变能:

(13)

体积分域Ω根据等效三维板的实际体积决定.将式(11)、(12)代入式(13)中,可进一步将弹性应变能整理成关于未知系数a的二次型形式:

(14)

其中:

(15)

若在与叶片与叶冠相连的面上施加外力f,产生位移u,则外力对等效三维板的做功大小为:

(16)

其中:

(17)

面积分域S由等效三维板受力面的实际大小决定.若在与叶片与叶冠相连的面上施加外力矩m,产生转角θ,则在计算做功时,分别用m,θ替换式(16)中的f,u即可.

综上,可得环板受外力作用变形后的总势能表达式如下:

(18)

依据最小势能原理的驻值条件[19],可求得:

a(d11,d12,…,d66)=A-1b

(19)

将式(19)代入(10)中,得到仅含有未知弹性参数的位移表达式:

u(d11,d12,…,d66)=N(x,y,z)A-1b

(20)

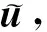
(21)

即可构造方程组,求解后得到待定弹性参数值,以此作为三维环板弹性参数的初值.

3 算例

算例的初始叶片组模型如图1,共含有72条叶片,每隔5°均匀分布.等效时,将每隔5°分布的单条叶片等效为占据5°的弹性板,如图6中所示环板上标注的5°扇区阴影区域.完成单个扇区的等效建模后,绕轴旋转复制71次即得到叶片组等效后的三维环板模型.

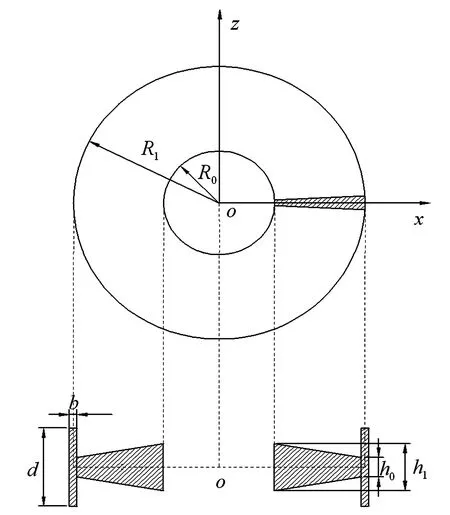
图6 等效叶片组的三维带冠环板几何尺寸示意图Fig.6 Geometric size diagram of three-dimensional annular plate of equivalent blade group

初始叶片组模型的几何与材料等物理参数值见表1,均采用国际单位制.

表1 叶片组模型物理参数表Table 1 Parameters of blade group

叶冠为各向同性的轴对称柱壳,几何与材料等物理参数值见表2,模型不需等效.

表2 叶冠模型参数表Table 2 Parameters of shroud

3.1 等效环板的厚度、密度

等效单条叶片的三维弹性板,密度ρ取为与初始叶片组相等,即ρ=ρb,y方向(径向)的长度Y为叶片内、外径之差,外缘z方向的长度Z可用弧长近似,即:

Y=R1-R0=0.1191m

Z≈R1θ=0.031m

(22)

式中θ=π/36,将表1数据代入公式(1)～(3)中,经计算可得等效环板的厚度分布函数为:

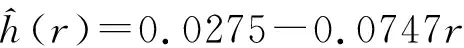
(23)

3.2 等效环板的弹性参数

基于第2节分析思路,首先确定材料坐标系与总体坐标系间的夹角α=66°.将α=66°代入转轴公式中,计算得总体坐标系下的刚度矩阵D为:

(24)

其中:

以下分别施加外力矩mz和外力fx,通过静力学等效求得d22、d44和d66的初值.

第一步,构造纯弯曲变形,确定d22.叶根固定,叶冠处受沿z方向的力矩:

(25)

静力分析后,初始单条叶片在xoy和yoz平面的变形如图7所示.黑色虚线为变形前叶片组位置,蓝色实线为变形后叶片组位置.可见,叶片x方向几乎无变形位移,在yoz平面的变形可近似看成欧拉梁,其中z方向的变形可用二次函数模拟,因此可设等效三维板的位移场为:

(26)

将式(25)、(26)代入(10)～(20)可得等效板的位移场表达式,其中包含了待定弹性参数d22.

(27)

将等效环板最大y坐标所在平面上的中心点坐标和位移数值代入(27),可求解出d22,结果为:

d22=2.9×1012Pa

(28)

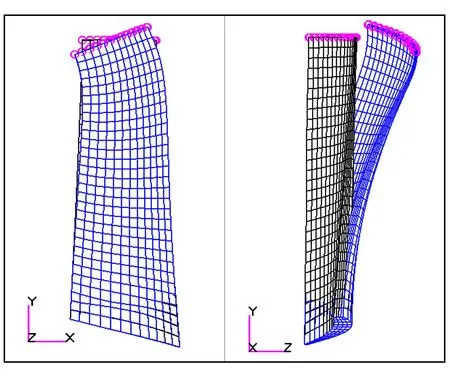
图7 受外力矩作用的叶片xoy和yoz平面变形图Fig.7 Deformation diagram of blade under moment in the plane of xoy and yoz

第二步,构造纯剪变形,确定d44和d66.叶根固定,叶冠处受沿x方向的外力:

(29)

静力分析后,初始单条叶片在xoy和yoz平面的变形如图8所示.黑色虚线为变形前叶片组位置,蓝色实线为变形后叶片组位置.

可见,叶片在y方向无位移,x,z方向的变形可用三次函数模拟,故设等效板的位移场为:

(30)

将式(29)、(30)代入式(10)～(20)可得关于d44,d66的位移表达式,将等效环板最大y坐标所在平面上的中心点坐标和位移数值代入可求得:

d44=6.5×1014Pa

d66=1.9×107Pa

(31)

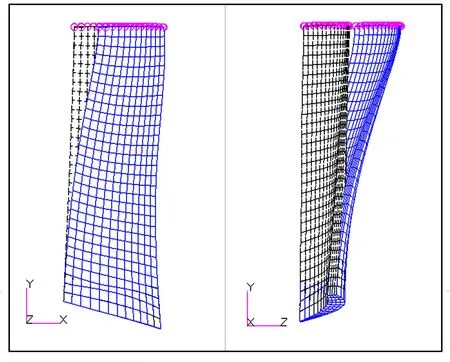
图8 受外力矩作用的叶片xoy和yoz平面变形图Fig.8 Deformation diagram of blade under moment in the plane of xoy and yoz

参见第2.1节式(8)、(9),可将d11,d12的初值取为:

d11=d22=2.9×1012Pa

d12=1.1×1012Pa

(32)

根据式(7)、设置设计变量的可行域,建立数学规划模型.

s.t.d∈[106,1015]×[106,1015]×

[106,1015]×[106,1015]×[106,1015]

(33)

其中,d={d11,d12,d22,d44,d66},将式(28)、(31)和(32)中的数据作为初值,利用MSC.Nastran的动力优化功能[20]得弹性参数终值.迭代计算后可确定环板弹性参数的终值为:

d11=d22=4.1×1012Pa

d12=3.5×1010Pa

d44=8.2×1014Pa

d66=6.1×107Pa

(34)

利用上述方法求得三维环板建模所需的全部几何、材料参数后,可在Patran中建立环板的有限元模型,将等效三维环板模型与初始轮盘组合后可得到三维叶盘缩聚模型.

3.3 等效结果与分析

模态分析后得到的叶盘缩聚模型与初始叶盘模型的0、1节径模态变形云图如图9,可见模态变形的横向等位移线基本一致.

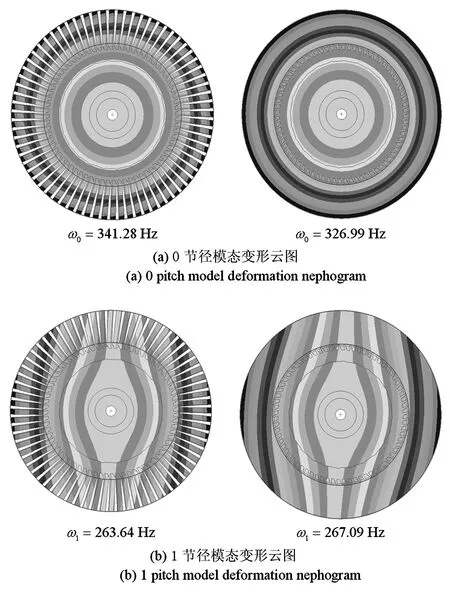
图9 初始与三维叶盘缩聚模型模态云图对比Fig.9 Comparison of modal deformation nephogram for initial and reduced bladed disk

利用两种模型计算得到的固有频率结果如表3,其中0节径和1节径的固有频率相差分别为-4.18%和1.31%.算例中,初始叶盘模型为回转周期结构,模态分析需用到单个扇区的模型,节点数目约为3100；等效后的缩聚模型为轴对称分布,模态分析时仅需用到子午面的模型,节点数目不足350,可大大降低模型动力学分析时的自由度数目,达到高效计算的目的.

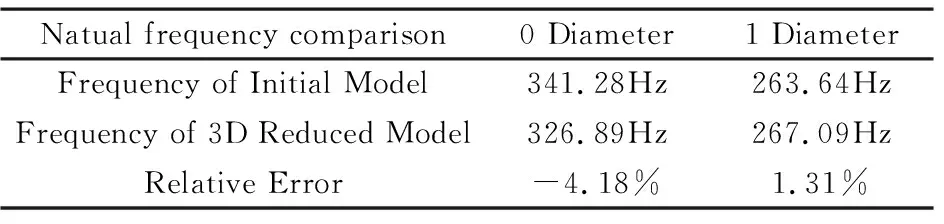
表3 初始与三维板缩聚模型固有频率数据结果Table 3 Natural frequencies of initial and reduced model

文章[18]建立的二维叶盘缩聚模型与本文建立三维叶盘缩聚模型模态变形后的单元轮廓对比图如图10所示,黑色线条和蓝色线条分别为模态变形前、后的单元轮廓线,可见,三维叶盘缩聚模型与二维叶盘缩聚模型相比,更能正确表现叶片-轮盘的轴向-周向振动耦合效应.分析表明,文中的等效建模方法能相当可观的降低叶盘整体有限元分析的自由度数目,且用缩聚模型计算得到的低阶振动固有频率具有的足够精度.

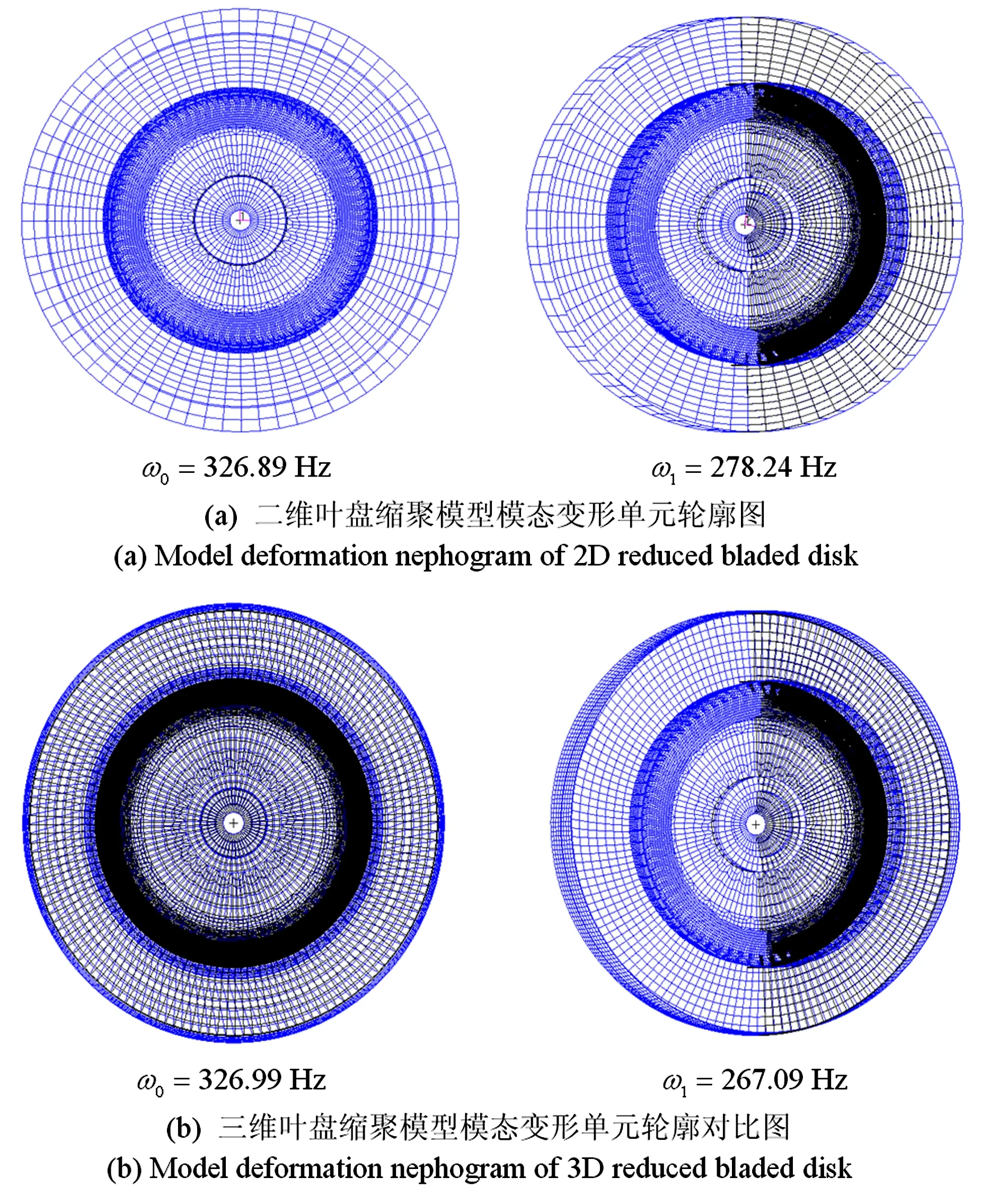
图10 二维与三维叶盘缩聚模型模态变形单元轮廓图Fig.10 Comparisonof modal deformation nephogram for 2D & 3D reduced bladed disk

4 结语

在较小的尺度上,叶片组是由叶片按照固定回转角度沿周向对称排列的周期性重复结构.在较大的尺度上,这种周期性重复结构可以被近似地均质化,这样可使得分析和计算难度大大降低.对于叶片组的等效建模思路,本文选用各项异性环形板等效周期性重复的叶片组三维有限元模型,在保证两种模型外观特征尺寸一致、整体质量和惯量相同的条件下,通过调节等效环板模型的弹性模量等参数,使得初始模型和等效模型的主要固有频率和模态具有相似的特征.

实现模型的等效时,综合运用了弹性力学中的最小势能等原理,给出了具有可操作性的确定等效模型参数的方法,并以航空发动机带叶冠的低压涡轮叶片-轮盘模型为具体应用实例,展示了模型等效的步骤.对于设计状态已确定的单级叶盘,等效的环板和轮盘组合体具有轴对称特点,故计算效率高,可直接应用于转子的整体动力学计算,也可为转子系统的优化设计等应用提供精度和效率兼顾的弹性叶盘缩聚模型.