压电复合材料悬臂板1∶3内共振的非线性动力学分析*
杨佳慧 张伟 袭安
(1.北京工业大学 机电学院, 北京 100124) (2.北京农业职业学院, 北京 102208)
引言
实际工作环境中,飞行器机翼是复杂的非线性系统,传统分析方法是忽略系统控制方程中的非线性项,利用线性系统近似描述工程问题,但在工程应用中发现,这样的研究结果与实际相差甚远,因此选择合适的方法对其进行研究是很重要的.对于大多数非线性系统的运动控制方程而言,由于非线性项的存在和复杂的边界条件,使得求其精确解几乎是不可能的,因此只能用数值方法或者是近似解析方法来研究.
摄动方法就是近似解析方法的一种,它是重要的求解非线性方程的数学工具.多尺度法是摄动法的一种,自20世纪60年代以来多尺度法经过Nayfeh[1,2]等人的发展与完善,成为很有效的近似分析方法,已被广泛的应用于各种非线性问题的分析中.多尺度法的基本思想是根据变量的变化不同,来区分快慢时间尺度,将响应的展开式考虑成为多个时间变量,即多个时间尺度的函数,而不是单个时间变量的函数.多尺度法具有很多优点,可以方便地处理多种类型的非线性系统,它既能计算周期运动也能分析衰减振动,既能分析稳态响应,也能用于非稳态过程的研究中.
1998年Abe[3,4]分析了在四边简支矩形层合板受到谐波激励时的非线性动力学,用多尺度法分析了系统的稳态响应,得到了激励的振幅和线性固有频率在三阶Galerkin离散下的关系.2008年Hao[5]等人利用高阶板壳理论和多尺度法研究了面内激励和横向外激励联合作用下四边简支矩形功能梯度板的非线性动力学行为.2009年Nejad[6]等人研究了粘弹性悬臂板的非线性振动行为,利用多尺度和摄动方法对系统进行了分析,研究了系统的混沌运动,分叉等现象.2013年陈建恩[7]等人应用多尺度法得到了横向载荷和面内载荷联合作用下四边简支点阵夹芯板的平均方程.通过数值方法研究了不同共振情况下点阵夹芯板的非线性振动响应.2017年郭翔鹰[8]等人将机翼简化为压电纤维复合材料悬臂中厚壳模型,采用多尺度法得到极坐标形式的平均方程.通过数值方法得到了中厚壳结构的幅频响应曲线、分叉图等.
以上文献建立的动力学模型多为简支板模型,悬臂板较少,而压电复合材料层合悬臂板模型未见.本文以飞行器机翼为工程背景,在推导出压电复合材料悬臂板的无量纲非线性偏微分方程的基础上,将系统离散为两自由度的非线性常微分方程;运用多尺度法进行摄动分析,推导出系统四维直角坐标形式的平均方程;使用MATLAB软件分析了横向外激励幅值和压电参数项对复合材料悬臂板在主参数共振-1∶3内共振情况下的非线性动力学响应.
1 基本方程
将飞行器机翼简化为复合材料层合悬臂板,建立力学模型如图1所示.悬臂板由三层材料组成,中间为基底层,材料选用石墨/环氧(HT3/QY8911)树脂,上下两层为压电薄膜(PVDF)层.悬臂板总的长、宽、厚分别为a,b,h,建立直角坐标系在板的中面,OB方向为x方向,OA方向为y方向,板受横向激励F0+F1cos(Ω1t)和面内激励p0+p1cos(Ω2t)的作用.

图1 复合材料层合压电悬臂板的力学模型Fig.1 Mathematical model of a cantilevered piezoelectric plate
根据经典板理论[9]及Hamilton原理,得内力表示的压电复合材料层合悬臂板的控制方程如下:
(1a)
(1b)
(1c)
式中:
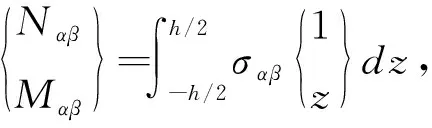
(2)
(3)
压电复合材料层合悬臂板内力与应变关系为:
(4)
其中,
(5)
式(5)中(Qij)k为第k层材料的刚度系数.
将式(4)带入到式(1)中,得到广义位移表示的压电复合材料层合悬臂板的控制方程如下:
(6a)
(6b)
(6c)
引入无量纲变换如下式:
(7)

(8a)
(8b)
(8c)
上式中系数的表达式见附录.
利用Galerkin方法,采用悬臂梁和自由梁的模态函数的组合作为悬臂板的模态函数[10],系统第一、二阶无量纲模态函数形式如下:
w0=w1(t)α1β1+w2(t)α1β2
(9)
式中u1(t)表示x方向的第一阶振幅,v1(t)表示y方向的第一阶振幅,w1(t),w2(t)分别表示横向即z方向的第一、二阶振幅,αi,βi的表达式如下:
α1=coshk1x-cosk1x-φ1(sinhk1x-sink1x)
β1=coshm1y+cosm1y-φ1(sinhm1y+sinm1y)
β2=coshm2y+cosm2y-φ2(sinhm2y+sinm2y)
(10)
忽略(8a)(8b)方程的所有惯性项和(8c)关于u0,v0的惯性项,利用Galerkin方法,将(9)和(10)代入方程(8),得压电复合材料层合悬臂板的两自由度的非线性常微分方程如下:
q3w12w2+q4w22w1+q5w13+q6w23=f1cosΩ1t
(11a)
r3w22w1+r4w12w2+r5w23+r6w13=f2cosΩ1t
(11b)
2 摄动分析
由于多尺度法是求解非线性系统很有效的近似分析方法,因此应用多尺度法对压电复合材料层合悬臂板两个自由度非线性常微分方程(11)进行摄动分析,引入如下的尺度变换:
μ1→εμ1,μ2→εμ2,q1→εq1,qp→εqp,q2→εq2,
q3→εq3,q4→εq4,q5→εq5,q6→εq6,r1→εr1,
rp→εrp,r2→εr2,r3→εr3,r4→εr4,r5→εr5,
r6→εr6,f1→εf1,f2→εf2
(12)
将变换公式(12)代入方程(11)得含小参数ε的方程:
εq2w2+εq3w12w2+εq4w22w1+εq5w13+εq6w23
=εf1cosΩt
(13a)
εr2w1+εr3w22w1+εr4w12w2+εr5w23+εr6w13
=εf2cosΩt
(13b)
为了获得压电复合材料层合悬臂板的四维平均方程,假设方程(13)有如下形式的解:
w1(t,ε)=x0(T0,T1)+εx1(T0,T1)
(14a)
w2(t,ε)=y0(T0,T1)+εy1(T0,T1)
(14b)
其中T0=t,T1=εt.
考虑主参数共振和1∶3内共振,则有如下形式的内共振关系:
Ω1=Ω2=Ω=ω,ω2≈3ω1
(15)
式中ω1和ω2为相应线性系统的第一阶和第二阶固有频率,σ1和σ2为系统的调谐参数.
把式(14)和(15)代入式(13),并且比较方程两边小摄动参数ε同阶次的系数,得到下面的微分方程:
ε0阶 :
(16a)
D02y0+ω2y0=0
(16b)
ε1阶:
= -μ1D0x0-σ1x0-2D0D1x0-(q1+qp)x0cosωt-
q2y0-q3x02y0-q4y02x0-q5x03-q6y03+f1cosωt
(17a)
D02y1+ω2y1
= -μ2D0y0-σ2y0-2D0D1y0-(r1+rp)y0cosωt-
r2x0-r3y02x0-r4x02y0-r5y03-r6x03+f2cosωt
(17b)
将方程(13)的解用复数形式表示为:
(18a)
(18b)

将方程(18)带入方程(17),得下式:
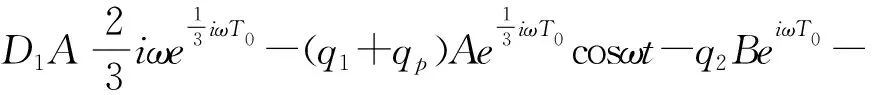
(19a)
D02y1+ω2y1=-μ2BiωeiωT0-σ2BeiωT0-
(19b)
式中的符号cc和NST分别表示方程(19)右边函数的共轭项和非长期项,令方程(19)的长期项等于零,可以得到复数形式平均方程如下:
(20a)
(20b)
令A=x1+ix2,B=x3+ix4,代入(20)得直角坐标形式的四维平均方程:
(21a)
(21b)
(21c)
(21d)
3 数值模拟
本节在得到压电复合材料层合悬臂板四维直角坐标平均方程(21)的基础上,选取无量纲横向激励幅值f2和压电参数项qp作为控制参数,基于四阶Runge-Kutta法,利用MATLAB软件对主参数共振-1∶3内共振情况下的压电复合材料层合悬臂板进行数值模拟分析,得到系统的非线性动力学响应.
3.1 横向外激励幅值对系统非线性振动特性影响
由于横向外激励幅值是影响系统非线性振动响应最重要的因素之一,所以首先研究f2对系统的影响.选取系统初始条件和参数值为:
x10=-0.23,x20=-0.48,x30=0.02,
x40=-0.01,μ1=0.02,μ2=0.04,
σ1=0.25,σ2=0.37,q1=4.5,qp=3.7,
q3=6.3,q4=0.7,q5=6.4,r1=1.2,
rp=6.4,r4=0.45,r5=0.31,r6=4.9
(22)
将式(22)的值代入到方程(21),采用MATLAB软件,通过数值模拟,得到系统随横向外激励幅值f2变化的分叉图如图2所示.由图可以看出,系统存在周期和混沌运动,并且周期与混沌交替出现,且混沌幅值远高于周期的幅值.当无量纲的横向激励幅值从84变化到97时,系统依次呈现单倍周期→混沌→单倍周期→混沌→单倍周期的变化规律.
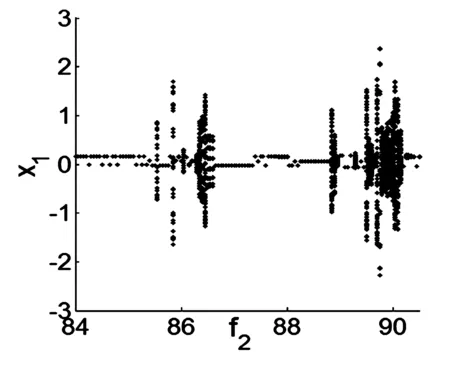
图2 系统随横向激励幅值变化的分叉图Fig.2 Bifurcation diagrams of system amplitude f2with the change of transverse excitation
为了验证分叉图的正确性,取f2=85,绘制系统前两阶波形图、相图、庞加莱映射如图3所示.由图可以看出,系统运动呈现为单倍周期运动.
由分叉图可以看出,当系统发生混沌时,系统幅值会发生大幅跳跃,运动形式由单倍周期转换为混沌形式.当取f2=90时,绘制前两阶的波形图、相图、庞加莱映射如图4所示,由图4看出系统的运动确实为混沌运动.

图3 单倍周期运动Fig.3 Periodic motion of the plate when f2=85
3.2 压电参数项对系统非线性振动特性影响
为了分析压电材料在系统振动过程中对系统非线性响应的影响,选取另一组初始条件和参数值如下:
x10=1.4,x20=2.7,x30=0.05,x40=-0.09,
μ1=0.02,μ2=0.04,σ1=7.5,σ2=9.3,q1=11.2,
q3=6.3,q4=31.6,q5=1.4,r1=1.2,rp=9.7,
r4=6.1,r5=5.6,r6=2.7,f2=85
(23)
取压电参数项qp从0变化到15,得到系统的分叉图如图5所示.由图可知,随着压电参数项的增大,系统由三倍周期运动逐渐变为分叉运动,最后呈现为混沌运动,因此压电参数项对系统的非线性振动响应有很重要的调节作用.
4 结论
本文研究了在横向激励和面内激励联合作用下,压电复合材料层合悬臂板的非线性动力学响应.应用经典板理论和Hamilton原理建立系统无量纲偏微分动力学方程,采用Galerkin方法对系统进行二阶离散,得到两自由度的无量纲常微分方程.

图4 混沌运动Fig.4 Chaotic motion of the plate when f2=90

图5 系统随压电参数项变化的分叉图Fig.5 Bifurcation diagrams of system coefficient qp with the change of piezoelectric
考虑主参数共振-1∶3内共振,运用多尺度法进行摄动分析,推导出四维平均方程.选取一组合适的参数,数值模拟得到横向外激励幅值对复合材料悬臂板非线性动力学响应的影响.结果表明当无量纲的横向激励幅值从84变化到97时,系统存在周期和混沌运动,并且周期与混沌交替出现,且混沌幅值远高于周期的幅值.
选取另一组参数值,绘制出了系统幅值随压电参数项变化的分叉图,由图可知压电参数项对系统的非线性振动响应有很重要的调节作用.因此,在实际工程中,可以通过改变系统外激励幅值或压电参数项,来调节系统振动的幅值,保持系统振动的稳定性.

