需求依赖库存时基于回购契约的供应链协调研究

高 婷,叶涛锋

(江苏科技大学 经济管理学院,镇江 212003)

在现实生活中,类似于大型超市、百货店的商家们总是在一定的空间内堆满更多的商品，以吸引消费者购买,学者们将这一现象称为库存水平影响需求,并对其进行研究,结果发现在一定的范围内库存水平对市场需求确实有着正向促进作用[1-2]．而针对库存水平影响需求的形式,主要可以归纳为两类:初始库存量对商品市场需求的影响和随时间变化的瞬时库存量对市场需求的影响[3]．随着相关研究的深入,需求依赖于库存水平更多被学者们引入到供应链协调的研究中．比如文献[4-5]中采用随机需求函数为α+βQ+ε,α>0,β>0的模型以及Di=ai-bpi+γpj+cQi+ε研究了单个供应商和单个供应商组成的供应链协调问题．虽然学者们将需求依赖于库存水平广泛应用于供应链优化问题的研究,但都是假设供应链中的成员为风险中立型决策者．但是,现实生活中,决策者在决策时往往对风险保持规避的态度．比如,文献[6]中基于条件风险价值(conditional value-at-risk，CVaR)准则,研究了缺货惩罚成本对于风险规避型零售商的影响;文献[7]中则结合不同测量风险的方法,对比风险中立型报童模型和风险规避型报童模型下的最优订货量，得出在不考虑商品产值和缺货惩罚成本情况下,风险规避型决策者的最优订货量比风险中立型决策者的最优订货量少．近年来,供应链中的风险管理问题受到了广泛关注．文献[8]中在考虑市场需求是库存水平线性分段函数、变质性产品以及零售商采用(S,s)订货策略的情形下,给出了可以实现供应链完美协调的数量折扣策略．文献[9]中研究表明零售商的风险厌恶加剧了双重边际效应,恶化了供应链效益．文献[10]中则利用条件风险价值理论(CVaR) 探讨随机需求下供应链系统中各参与者均具有风险规避特性时,供应链系统在回购契约下的优化与协调问题．文献[11]中运用CVaR方法,考察了风险中立型供应商和风险规避型零售商联合促销报童类商品时,如何运用回购契约实现供应链协调等问题．文献[12]中则在条件风险估值风险度量准则下，以权衡期望利润和CVaR利润(均值-CVaR)，分析了调整后的保险契约在协调供应链方面的应用.

总结相关文献发现,大多数文献对于供应链协调机制的研究通常不考虑需求对于库存水平的依赖性,或者不考虑供应链系统中各成员的风险态度．基于以上问题,文中从不同的角度对经典报童模型进行扩充,将库存水平对于需求的影响作为基本假设,同时将条件风险价值和期望利润的加权平均作为零售商的风险度量[12]，以此引入零售商的风险规避态度,研究单个风险中立型供应商和单个风险规避型零售商组成的二级供应链协调以及优化问题,并给出了协调机制．

1 问题描述及假设

1.1 模型描述

文中主要研究一个风险中立型供应商和一个风险规避型零售商组成的二级供应链优化及协调问题．该供应商主导的Stackelberg模型中,供应商主要生产单一的短生命周期产品，其成本为c,供应商将在销售季节开始前公布单位产品的批发价格w．零售商以此为依据来订购q单位的该产品,然后以p单价销售给市场中的顾客．假设零售商面临的市场需求是初始库存水平的线性函数，即d=α+βq+ε,α>0,0<β<1.其中ε≥0 是随机需求变量,独立于库存水平,其概率密度函数和分布函数分别为f(·)和F(·)．期末,供应商的剩余产品以单价r的残值进行处理.为保证参数的选择符合实际情况,应满足p>w>c．πr,πs和πsc分别为零售商、供应商以及供应链的利润．

1.2 风险测量

以经典的报童模型的期望利润为目标函数,假设零售商处于理性状态,对风险持有中立的态度,即完全不考虑零售商的风险态度,而这样的理想状态在现实情况下很难达到．因此,文中为了更好地模拟现实情境,在目标函数中引入风险系数,用条件风险价值(CVaR)的测量方法来度量风险．但是,CVaR准则测量风险的方法通常把高于置信水平的利润也看作是风险,因此会低估利润．所以,为克服这一弊端,文中依据文献[13]中提出的以CVaR与期望利润的加权平均作为风险规避型零售商的效用(即CVaR-利润)来平衡风险，更加符合现实情境．此时目标函数为:

(1-λ)CVaRη[πr(q)]+λE[πr(q)],λ∈[0,1]

式中：φ为决策者的目标利润；η∈(0,1]为决策者的风险厌恶程度；η取值越小则表示决策者对于风险的厌恶程度越大．

2 CVaR-利润下的最优订货策略

在单一的批发价契约下,零售商根据供应商给出的批发价格订购商品．期末,如果零售商供大于求,则未出售产品以单价r进行处理．那么,根据零售商的市场需求函数,其获得的利润为

πr(q)=pmin(q,d)-wq+r(q-d)+=(p-w)q-(p-r)[q-(α+βq+ε)]+

式中，min(q,d)=q-(q-d)+.相应地,供应商获得的利润为πs(q)=(w-c)q.

于是,基于文中采用的效用量度,风险规避型零售商的最优订货决策满足下列命题.

命题1基于供应商给出的批发价格w,零售商在CVaR-利润效用下的最优订货量为:

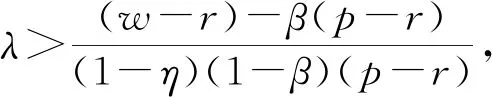
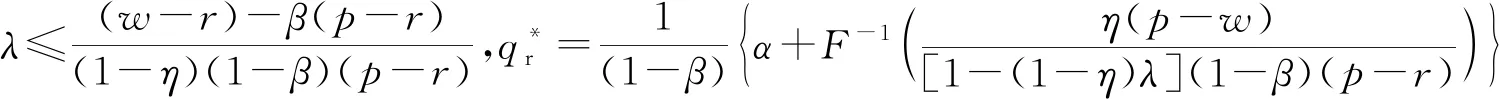
证明：由于

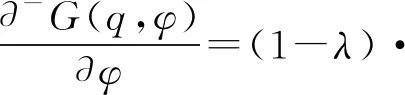
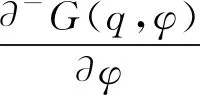
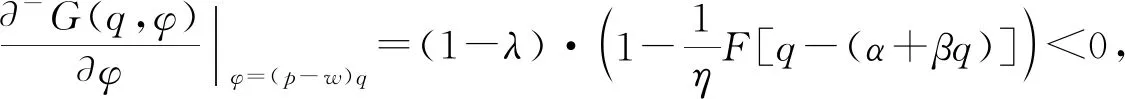
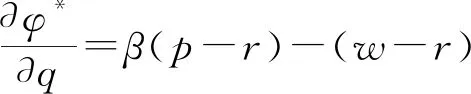
G(q,φ*)=(1-λ)·

λ(1-β)(p-r){1-F[q-(α+βq)]}

于是最大值点为：

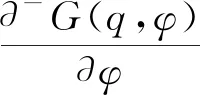
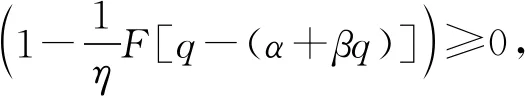
此时,

同理有:

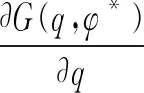
λ((p-w)-(1-β)(p-r)F[q-(α+βq)])=

于是最大值点为：

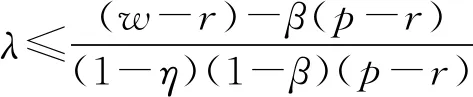
因此，在CVaR-利润效用下零售商的最优订货量为:

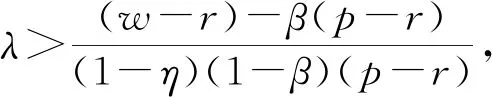
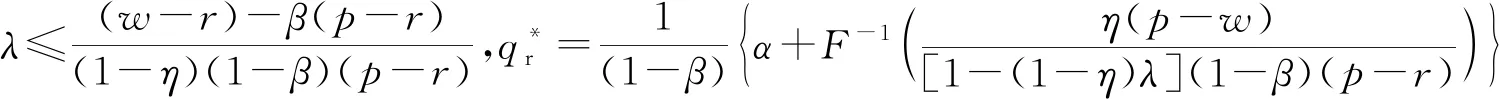
该命题证毕．

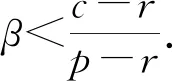
3 基于回购契约的供应链协调

由于单一的批发契约不能协调供应链,而大量的文献已经表明供应链给出的回购契约确实能够分担零售商的风险,实现供应链的整体优化．现实中,回购契约在以易逝品为产品对象的企业间应用比较广泛,比如影音、服装等行业．文中已经发现当需求依赖于库存水平时,单一的批发价契约也无法实现供应链的协调．这里,为了使零售商增加订货量，实现供应链的完美优化,供应商可以以回购单价b收购零售商未销售出去的商品,然后再以单价r对其进行残值处理．将上标B作为回购契约的情形．那么,根据回购合同(wB,b),零售商、供应商的利润函数则分别为:

此时,当零售商的风险中立时,基于期望利润最优的订货决策

而零售商是风险规避时,基于CVaR-利润准则下的最优订货决策满足下列命题．

命题2基于回购合同(wB,b),零售商在CVaR-利润效用下的最优订货量为:

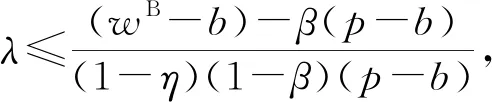
证明参照命题1

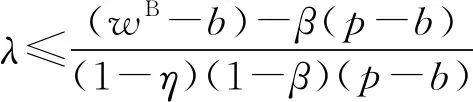
由该利润函数可知,当η<(p-c)/(p-r)(1-β),假设供应商的期望利润函数中批发价格的系数为κ1,于是有

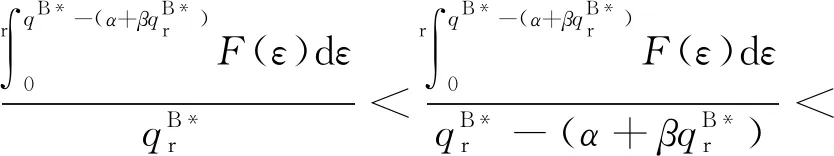
因此,κ1≥0恒成立．相似地当η≥(p-c)/(1-β)(p-r)时,批发价格的系数κ2≥0也成立．由此表明,当供应链获得最大利益时,供应商的期望利润与其给出的批发价格w成正比．也就是说,当供应商提供回购合同(wB,b)使供应链整体收益最大时,总利润可以在供应商和零售商之间任意分配．供应商可以提高批发价格来增加收益，但是具体的利益分配取决于和零售商之间的议价能力．

4 算例分析

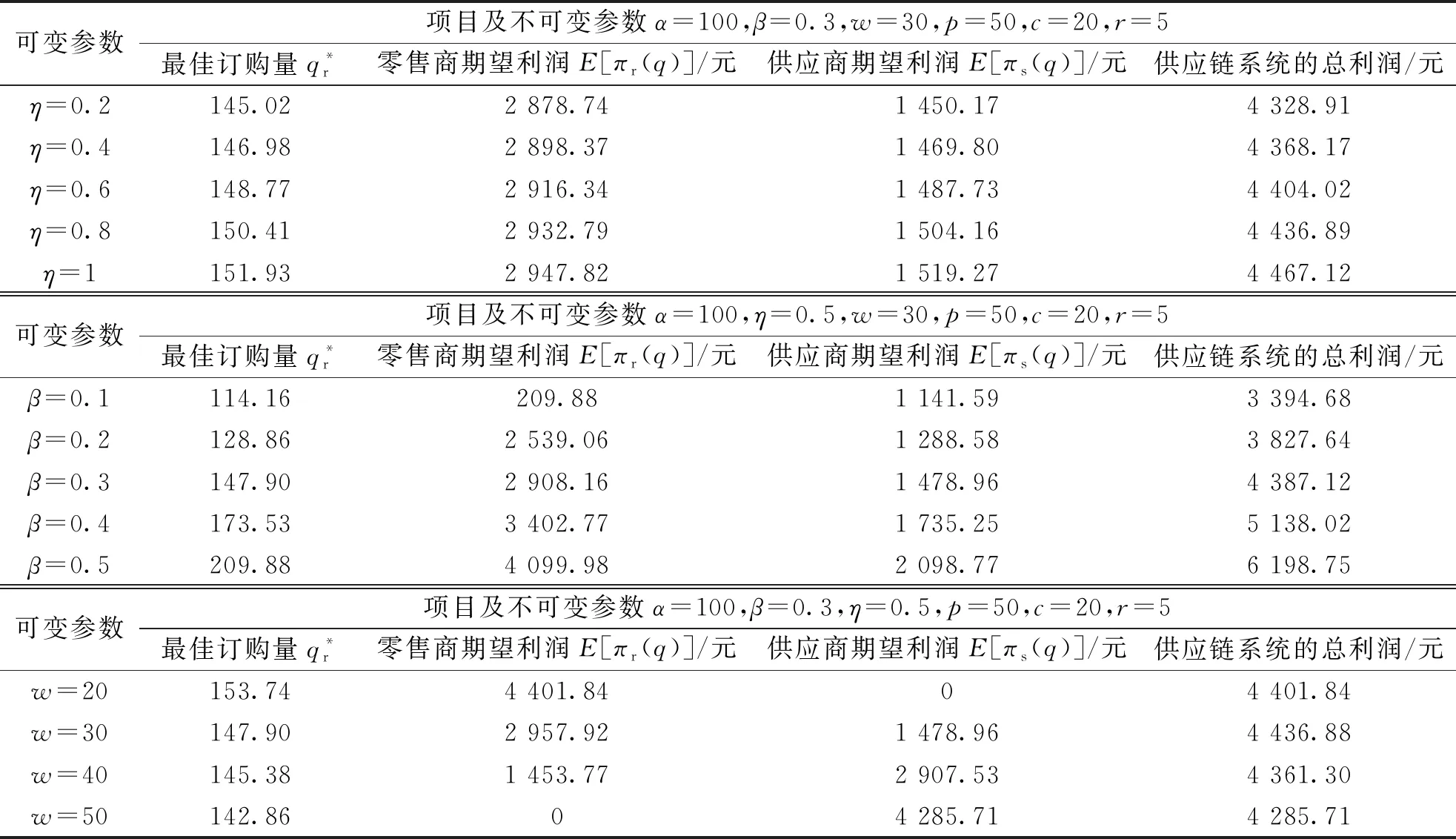
表1 批发价契约下的数值分析Table 1 Numerical analysis of whole-sale price contract

通过对表1的分析,可以得出：

(1) 独立的批发价契约无法实现供应链系统的完美优化．表1中,不同的参数组合下,分散决策下的零售商与供应商的期望利润之和总不超过集中决策下的供应链系统的最大收益,同时零售商的最佳订货量总低于集中决策下的供应链的最佳订货量,这说明独立的批发价契约并不能协调供应链．

(2) 独立的批发价契约下零售商的最佳订购量及期望利润随η和β增加而增加,随批发价w提高而降低．表1中,当其他参数保持不变时,零售商的最佳订货量以及期望利润随η上升而降低,也就意味零售商对于风险抱有躲避的态度,因此不愿意提高订货量，承担较高的风险,并且这样思维越保守，获得的销售收益会越来越少．同时,需求依赖于库存水平使得零售商的消费者需求增加,零售商也随之增加订货量以获得最多的利润．而供应商给出的批发价格相当于零售商的购货成本,与现实情况一样,订货成本高,预期的收益就低．

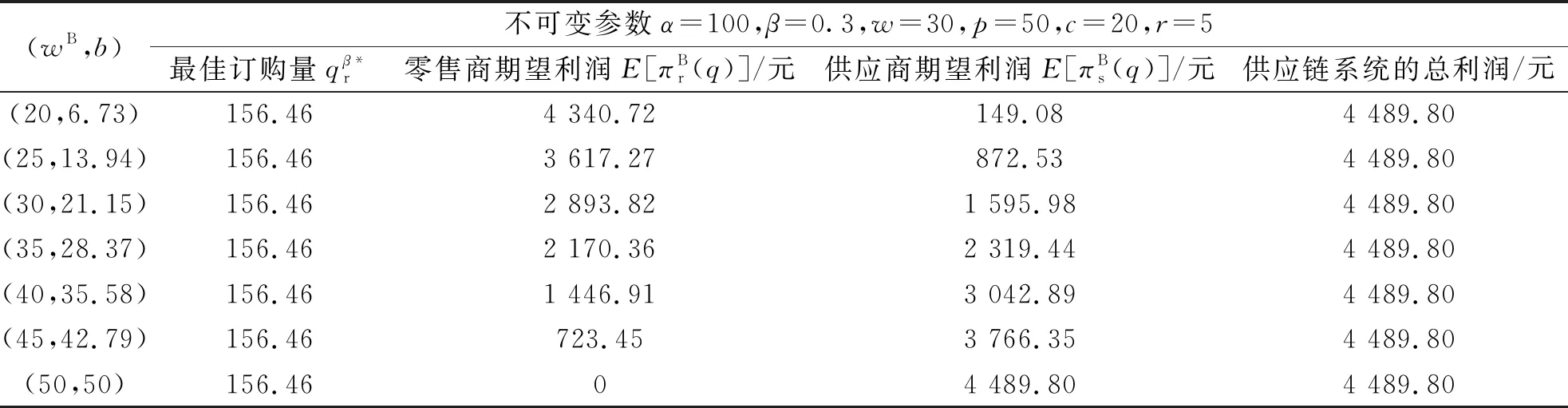
表2 回购契约下的数值分析Table 2 Numerical analysis of buy-back contract

假设的二级供应链系统的组成结构中，供应商作为博弈的主导者,其制定的回购契约不受零售商订货数量的干扰,具有一定的主动性．因此,只要给出的契约参数满足命题3给出的条件,那么满足条件的回购契约并不是唯一的．对比表1、2可以看出,在固定的参数下,合理的回购契约能够使得供应链的总收益增大,同时随着给出的批发价和回购价越来越高,供应商作为博弈的主导者其获得的利润越来越大．但是,零售商作为回购契约的接受者可以接受也可以拒绝．总之,想要多分得利润就要提高自身的谈判能力了．

5 结论

文中研究了单个风险中立型供应商和风险规避型零售商构成的供应链优化问题,该零售商面临的市场需求主要依赖其销售商品的库存水平．因此,在以CVaR-利润为效用函数基准下,文中得出结论:

(1) 单一的批发合同不仅不能协调供应链,而且零售商的风险规避恶化了供应链的效益;

(2) 合理的回购合同能够使供应商主动分担零售商的风险,引导零售商增加订货量,最终实现供应链的完美优化；

(3) 供应链的总利润根据各自的讨价还价能力，可以在零售商和供应商之间任意分配．

文中给出了供应链达到优化状态下契约参数满足的条件,为供应商提供了具体的决策方案,但是文中对于供应链系统中只有单一零售商的假设限定了该协调机制的适用范围,未来应在多零售商参与竞争方面深入研究,以便进一步贴近现实情境从而更好为决策者提供合理的协调机制．