钝体滑行艇喷溅阻力计算方法研究

凌 杰,王 毅,窦 朋,王志东

(1.陆军军事交通学院 镇江校区,镇江 212003)(2.江苏科技大学 船舶与海洋工程学院,镇江 212003)

船舶高速航行时,船体受到的动载荷和运动响应具有复杂的强非线性特性,包含了水动力和气动力耦合作用、自由面变形流动分离、航行的纵向稳定性、随浪中的横甩、底部砰击与舷侧喷溅等瞬态非线性问题,而钝体滑行艇在水中的运动会引起周围压力场的剧烈变化,如果采用合适的线型来充分利用这种流体动压力场,使其在铅垂方向上产生足够大的压力分量来支持部分或全部重量,使船的吃水和湿表面积减小,可以大大降低高速运动时的阻力[1-5]．因此,研究钝体的水动力特性及喷溅特性对滑行艇及其他高性能船舶的水动力性能及运动预报具有非常重要的理论意义和工程实用价值．文献[6]中通过模型拖航实验研究了棱柱型滑行艇不同底部斜升角下喷溅边线的形状及摩擦阻力的计算方法．文献[7]中提出了一种定量计算高速滑行艇须状喷溅阻力的方法,并将其描述为底部斜升角、纵摇角及航速的函数,预报结果表明,须状喷溅阻力约占总阻力的15%,与模型试验值相吻合,为滑行艇喷溅阻力的计算提供了一种有效的方法．文中基于FINE/Marine软件对不同工况下3种钝体滑行艇进行数值模拟,研究了钝体滑行艇的喷溅阻力计算方法．

1 计算模型

1.1 几何模型

钝体主尺度见表1．利用三维建模软件Solidworks建立3种钝体模型．坐标原点位于钝体尾部最底端,X轴位于中心线，指向钝体首部为正;Y轴指向左侧为正;Z轴垂直于水线面,向上为正．模型纵倾角即艉倾为3.0°,3种钝体的三维模型如图1．

表1 钝体模型主尺度Table 1 Main dimensions of bluff bodys

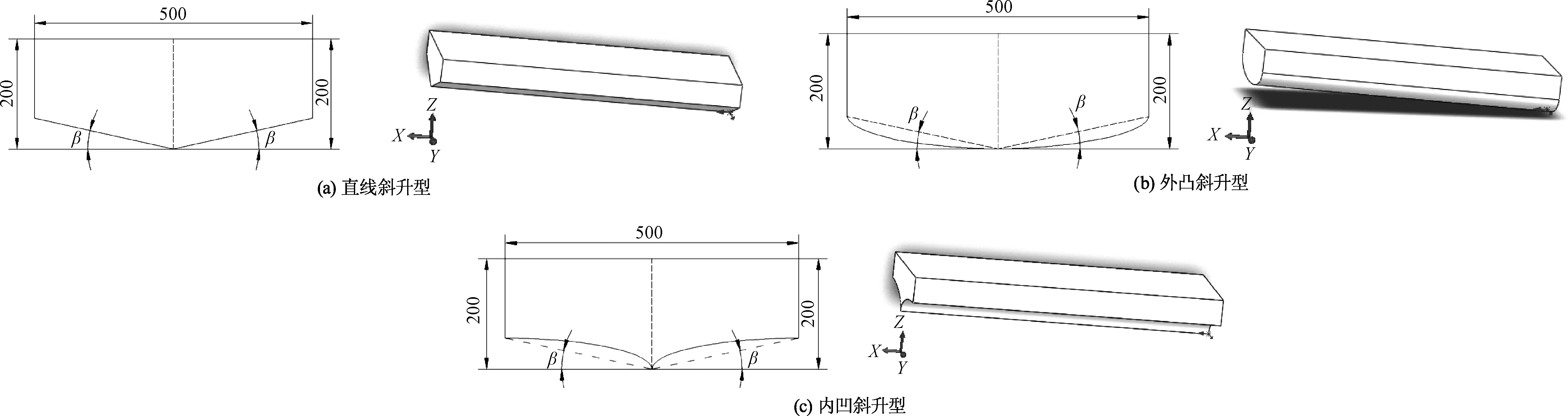
图1 三维钝体模型及坐标系(单位：mm)Fig.1 3D bluff bodys model and coordinate system(Unit：mm)

1.2 计算工况

钝体的长度傅汝德数Fr=0.54,纵倾角为3°．针对静水约束模式3种不同钝体、4种横向斜升角共计12 个工况,进行数值模拟，工况具体参数如表2．

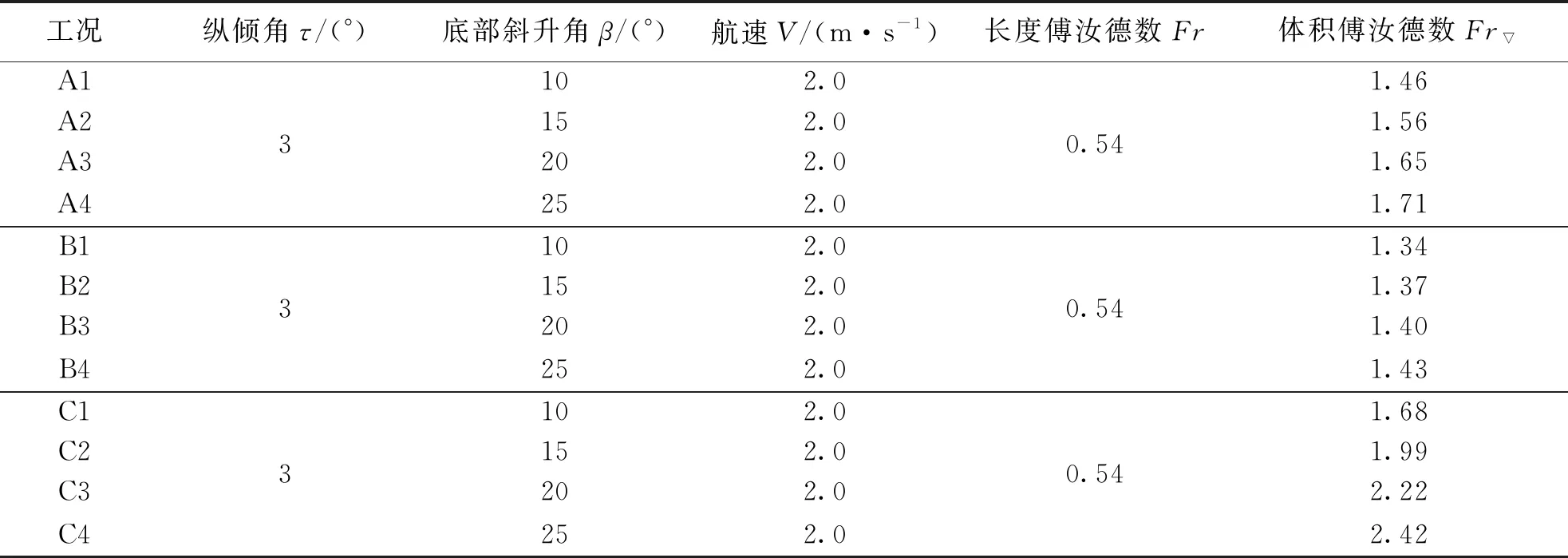
表2 计算工况Table 2 Calculated conditions

1.3 数值计算方法

FINE/Marine是一款由NUMECA公司为船舶与海洋工程设计的CFD软件包,图2为主要软件构成与操作流程，该软件包括了网格生成器HEXPRESS、粘性流场求解器ISIS-CFD和后处理工具CFView．对于船舶工程问题的模拟都可以通过使用FINE/Marine界面的设置计算实现,无需通过二次开发功能，为工程师提供了极大的方便[8-9]．

图3、4分别为HEXPRESS生成的A型钝体的整体网格和局部网格．

图3 整体计算域网格Fig.2 Meshes of the whole calculated domains

图4 中横剖面网格Fig.4 Meshes of the midbody section

文中基于CFD软件的钝体滑行艇静水约束模式下，三维数值模拟的参数设置为：三维非定常双相流,选用k-omega(SST-Menter)湍流模型,k与ω的值与雷诺数有关,采用滑行艇3个自由度运动,前进采用随体网格,升沉和纵摇采用弹簧法,控制方程采用中心差分格式离散,自由面采用混合自由面捕捉与重构相结合格式离散,压力速度耦合求解算法[10]．

2 喷溅阻力计算方法

图5中，艇体浸湿面被分为2个区域．

图5 滑行艇喷溅区域简化Fig.5 Planing craft simplified model and flow direction in spray zone

驻线OE到艇艉部区域被称为压力面Ap,它由浸湿龙骨线长Lk、浸湿舭缘线长Lc、艇浸湿宽度b及驻线OE围成;喷溅面As由驻线OE、喷溅前缘线OF及边线EF组成．作用在喷溅区域的动压小于滑行面的动压,却远大于空气作用在滑行艇表面上的动压,根据滑行艇不同纵剖线上除去水深影响的静压分布,可以找出不同纵剖线上O点,拟合出艇底的驻点线,即为喷溅后缘线OE,在这条线上流体压力最大,流速最小;再将滑行艇不同纵剖线上水相体积分布为0.5处拟合出艇底的喷溅边线,即为喷溅前缘线OF[11-14]．

基于Delaunay三角原理对喷溅区网格进行重构,保证非结构网格的规整性,在喷溅前、后缘线上插入边界点,边界点数据由面差值得到,确保网格质量和数据准确．喷溅阻力计算流程如图6[15]．

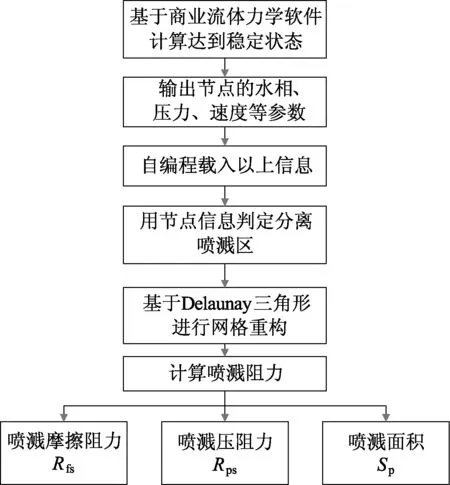
图6 喷溅阻力计算方法流程Fig.6 Flow chart of calculation method of spray resistance

喷溅总阻力:Rs=Rfs+Rps

(1)

喷溅摩擦阻力:

(2)

喷溅区摩擦阻力系数根据Davidson水池经验公式:

(3)

(4)

喷溅压阻力:

(5)

3 计算结果分析

图7为外凸斜升型滑行艇喷溅区分布，该图真实地反应了钝体在航行时发生的喷溅现象，当存在较大底部斜升角(β≥20°)时,钝体对水流阻碍作用降低,水流能量较小,未达到舷侧就已经衰减,喷溅区域呈现条带状．

图7 外凸型钝体不同底部斜升角的喷溅区域分布Fig.7 Spray region of β bluff body at different deadrise angles

直线斜升型钝体的喷溅后缘线为直线,与实验现象一致,而外凸斜升型和内凹斜升型呈现二次样条曲线形状;当底部斜升角较小(β≤10°)时,喷溅前缘线末端到达舷侧,并呈现直线状,喷溅现象明显,外凸形钝体相比之下更容易发生喷溅．

表3和图8分别为不同钝体在不同底部斜升角下的喷溅面积Sp与浸湿面积S0之比的变化曲线,喷溅面积由喷溅区内重构后的非结构网格面积相加得到,可见喷溅面积随底部斜升角增加而减小,是因为钝体底部斜升角增加后流体获得的能量减少,沿表面爬升衰减较快;直线斜升型钝体喷溅面积与浸湿面积比变化幅度最大,底部斜升角从10°增加到25°,Sp/S0由49%减少到了28%．

表3 不同钝体在不同底部斜升角下的喷溅面积Table 3 Spray area of three bluff bodys at different deadrise angles

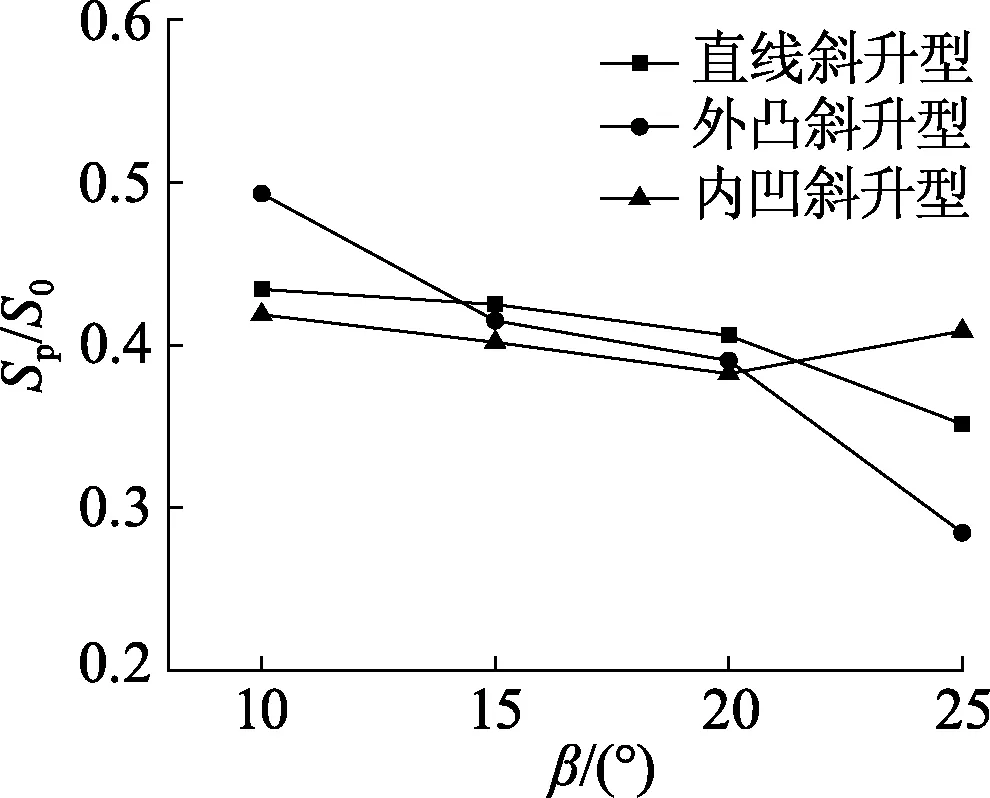
图8 不同钝体喷溅面积与浸湿面积之比Sp/S0的变化曲线Fig.8 Curves of ratio of different bluff bodys splash area and wet area Sp/S0

图9为不同钝体、不同底部斜升角喷溅底部边缘线长度Lw,由拟合后驻线在钝体尾部的横向长度获得,从图中可以看出：外凸斜升型钝体底部边缘线长度Lw变化稳定在0.2 m左右,直线斜升型和内凹斜升型钝体的底部边缘线长度随底部斜升角的增大而减小,在底部斜升角较大(β=10°)时,底部边缘线长度大于钝体半宽0.25 m,喷溅现象较为剧烈．

图9 不同钝体、不同底部斜升角喷溅底部边缘线长度LwFig.9 Bottom edge line length Lw of different bluff bodys at different deadrise angles

图10 不同钝体、不同底部斜升角喷溅摩擦阻力系数CfFig.10 Spray friction coefficient Cf of different bluff bodys at different deadrise angles

从图中可以看出：外凸斜升型钝体喷溅摩擦阻力系数Cf较稳定,直线斜升型和内凹斜升型钝体的喷溅摩擦阻力系数随底部斜升角的增大而增大,是因为直线和内凹斜升型钝体流速沿长度方向的分量随底部斜升角增加有显著提升;内凹斜升型钝体在β=25°时存在跳点,原因可能是此工况下喷溅区较小,截取纵剖面数量少,影响喷溅区捕捉．

图11为不同钝体、不同底部斜升角喷溅阻力RS的变化曲线,喷溅阻力由喷溅压阻力和喷溅摩擦阻力两部分构成,根据法向量获得每个非结构网格面压力沿速度方向的分量,求得喷溅压阻力,从图中可以看出：喷溅阻力随底部斜升角的增加而减小,外凸斜升型喷溅阻力最大,内凹型最小,是因为底部斜升角增加直接导致了喷溅面积的减小,以致喷溅阻力降低,外凸斜升型钝体对水流作用在沿速度方向的分量较大,水流在钝体首部堆积反作用在钝体上的力也越大,因此同Fr下外凸斜升型钝体喷溅阻力较大．

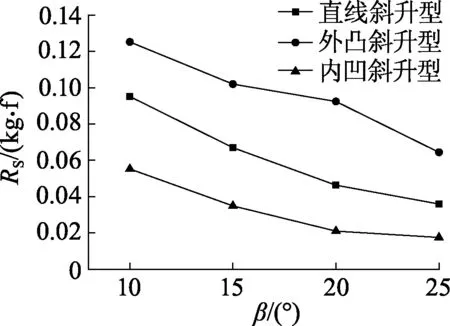
图11 不同钝体、不同底部斜升角喷溅阻力RS的变化曲线Fig.11 Curves of spray resistance RS of different bluff bodys at different deadrise angles

图12为不同钝体、不同底部斜升角喷溅阻力RS占总阻力R比值的变化曲线,可以看出：随着底部斜升角增加,外凸斜升型和直线斜升型钝体的喷溅阻力占总阻力的比值RS/R逐渐减少,说明总阻力中由喷溅阻力引起的成分随底部斜升角增加而减少,底部斜升角从10°增加到25°,外凸斜升型RS/R从14.0%减少到了9.5%,直线斜升型RS/R从13.8%减少到了11.7%;而内凹斜升型钝体喷溅阻力占总阻力的比值随底部斜升角增大而增大,并趋于稳定,底部斜升角从10°增加到25°,外凸斜升型RS/R从13.3%减少到了17.1%,可以看出在航速较低(Fr<2.0)时,钝体处于高速排水状态,内凹斜升型钝体不利于降低喷溅阻力占总阻力的成分．

图12 不同钝体、不同底部斜升角喷溅阻力占总阻力的比值RS/RFig.12 Ratio of spray resistance and total resistance resistance RS/R of different bluff bodys at different deadrise angles

图13为不同钝体、不同底部斜升角喷溅摩擦阻力Rfs占喷溅阻力RS的比值,可以看出：喷溅摩擦阻力占喷溅阻力Rfs/RS随底部斜升角增加而增加,并趋向一稳定值,在低体积傅汝德数(Fr<2.0)时,外凸型钝体喷溅摩擦阻力占喷溅阻力的比值最小,内凹型比值最大,原因是钝体底部外凸程度越大,流体作用在钝体沿长度方向的分量就越大,压阻力占阻力成分越大;底部斜升角从10°增加到25°,外凸斜升型Rfs/RS从34.5%增加到49.1%,直线斜升型Rfs/RS从40.2%增加到65.4%,内凹斜升型Rfs/RS从48.8%增加到69.4%．

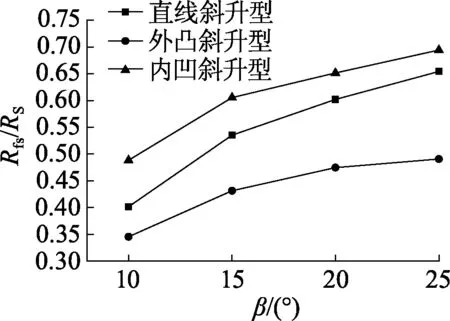
图13 不同钝体、不同底部斜升角喷溅摩擦阻力占喷溅阻力的比值Rfs/RSFig.13 Ratio of spray friction resistance and spray resistance Rfs/RS of different bluff bodys at different deadrise angles

4 结论

对不同钝体滑行艇进行三维建模,开展了长度傅汝德数Fr=0.54,底部斜升角β分别为10°、15°、20°、25°,静水约束中约束航行共12个工况下的数值模拟,得到以下结论:

(1) 当底部斜升角较大(β≥20°)时,水流未达到舷侧就已经衰减,喷溅区域呈现条带状,直线斜升型钝体的喷溅后缘线为直线,而外凸斜升型和内凹斜升型呈现二次样条曲线形状,与实验现象一致;当底部斜升角较小(β≤10°)时,喷溅前缘线末端到达舷侧,并呈现直线状,喷溅现象明显,外凸形钝体相比之下更容易发生喷溅;

(2) 随着底部斜升角增加,外凸斜升型和直线斜升型钝体的喷溅阻力占总阻力的比值RS/R逐渐减少,说明总阻力中由喷溅阻力引起的成分随底部斜升角增加而减少,底部斜升角从10°增加到25°,外凸斜升型RS/R从14.0%减少到了9.5%,直线斜升型RS/R从13.8%减少到了11.7%;钝体处于高速排水状态,内凹斜升型钝体不利于降低喷溅阻力占总阻力的比值．

(3) 在低体积傅汝德数(Fr<2.0)时,喷溅摩擦阻力占喷溅阻力的比值随着底部斜升角的增大而增大．其中外凸型钝体喷溅摩擦阻力占喷溅阻力的比值最小,内凹型比值最大,外凸斜升型Rfs/RS从34.5%增加到了49.1%,内凹斜升型Rfs/RS从48.8%增加到了69.4%．