CTOD尺寸效应的概率描述研究

陈春君,苗张木

(武汉理工大学 交通学院, 武汉 430063)

随着经济的发展、技术的进步,钢结构建筑朝着更高、更大、更厚的方向发展．结构越厚,内部出现缺陷(细小的孔洞和微裂纹)的可能性越大．这些缺陷在结构外载荷的作用下,会逐步演化成宏观裂纹,并极大地缩短建筑结构的使用寿命[1]．要保证结构不因裂纹问题而提前退役,就必须在设计阶段考虑材料抵抗裂纹扩展的能力．衡量材料抗断裂性能的指标有很多,如断裂韧度KC、G、CTOD、J．在这4个韧度指标中,裂纹尖端张开位移(CTOD)物理意义清晰、测试方法简单,应用比较广泛[2]．

在工程中,常常会遇到这样的问题:在设计阶段,需要对比不同建筑材料在设计厚度下的断裂韧度,并从中选出最合适的材料．在缺少实验数据的情况下,最稳妥的方法是测试所有备选建材在设计厚度下的断裂韧度值,用实验结果作为选择材料的依据．显然,这种方法不仅会增加设计成本,还会延长设计周期．若是能找到材料断裂韧度与厚度的关系式,并用已有的实验数据拟合出曲线,再在拟合得到的曲线上找到设计厚度下的韧度值,就能大幅度减少设计成本,并缩短设计周期[3]．

已有的研究发现,材料断裂韧性与试件厚度的关系,可用数学公式描述[4]．前人在使用该公式时,没有考虑韧度值的离散性,对实验数据粗糙地作均值处理,显然是不合理的．文中用概率论与数理统计的方法,对CTOD值的离散性进行研究,找到韧度值的合理分布模型,并从概率的角度,对尺寸效应作新的描述．另外,尺寸效应的原有公式在拟合精度上,有一定的提高空间．利用改进的公式,进一步提高了拟合性能．

1 尺寸效应公式

1.1 现有公式的改进

已有研究表明,当试件厚度较小时,断裂韧度与试件厚度成正比,试件越厚,韧度越大．当厚度继续增加,超过某一界限后,材料的断裂韧度会随着厚度增加而减小,并最终趋于常数,如图1[5-7]．

图1 断裂韧度与厚度关系Fig.1 Relationship between fracture toughness and thickness

文献[8]利用格里菲斯表面能理论和巴林布拉特吸附力理论,推导出了断裂韧度KC关于试件厚度的数学表达式:

KC=ξt1/2e-kt+KIC(1-e-kt)

(1)

式中:ξ,k,KIC为材料常数；t为试件厚度．为了验证上式的合理性,用LY12CZ(L-T)板材和TC4(L-T)板材的实验数据[9],采用最小二乘法进行曲线拟合．计算结果显示,LY12CZ(L-T)板材拟合曲线的最大误差为6.58%,TC4(L-T)板材的最大误差为2.41%．文献[10]用X140套管钢进行系列厚度的断裂韧度试验,并用上式拟合,误差同样很小．由此可见,式(1)能较好地描述断裂韧度KC的尺寸效应,且对于不同的材料均适用．

由KC与CTOD的关系[11],从式(1)推出了断裂韧度CTOD的尺寸效应公式:

δ=ξte-kth+δm(1-e-kth)

(2)

式中:ξ,k,δm为材料常数；h为调节参数．以20 ℃下,14MnNbp母材的CTOD试验数据为基础,用该式进行拟合,最大误差为15.6%,可见用式(2)描述CTOD的尺寸效应虽然合理,但其拟合性能有待提高．

δ=ξte-k1th+δm(1-e-k2th)

(3)

式中:ξ,δm为材料常数；k1,k2为调节系数．在曲线拟合时,其值由最小二乘法计算得到．改进公式使用时,有一个适用的厚度范围,该范围依赖于已知的数据．例如,已知某种材料在一系列厚度下的韧度值,将这些厚度按从小到大排列,可构成向量[t1,t2,t3…tn]．按式(3)进行拟合,则得到的曲线在区间[t1,tn]中,能保证结果的可靠,并且数据点越密,结果越有效．在该区间之外,因为缺少数据对曲线的约束,虽然拟合出的曲线经过该区域,但该段曲线是不能用来作韧度预测的．因此,改进公式在使用时,其适用范围是区间[t1,tn]．

1.2 CTOD的分布模型与K-S检验

大量试验结果显示,材料断裂韧度具有离散性．CTOD试验符合随机现象试验的特征,故而可用概率论与数理统计的方法对其进行研究．

文献[12]研究系泊链钢CTOD实验结果后,与正态分布发现相比,用威布尔分布对其进行描述更合适．文中假设韧度试验结果服从威布尔分布,分布函数如下:

F(x|a,b)=1-e-(xa)b

(4)

式中：a为尺度参数,b为形状参数．考虑到样本均值X是总体均值μ的无偏估计,样本方差S2是总体方差的无偏估计,联立

(5)

(6)

计算参数a,b的估计值,代入式(4)中得到分布函数的具体形式．

样本是否可用刚刚得到的分布函数描述其分布,需用假设检验来判定．由于试验所得的样本点少,特选用适合小子样的K-S检验方法来做判定．K-S检验是将变量的累计分布函数与假设分布进行比较．用Ai表示假设分布每个类别的累积相对频数,Oi表示样本频数的相应值,定义统计量k=max|Ai-Oi|．若每次抽样研究中,k值在0附近,则说明样本服从假设分布;若k值很大,就可以做出拒绝假设的判定．当判定接受原假设,就用假设的威布尔分布描述断裂韧度的分布．当判定拒绝原假设时,用最大似然估计得到参数a,b置信度为95%的置信区间,在置信区间内另找两点a2和b2,再进行K-S检验,如此反复,直到找到合适的参数a,b使得检验通过．

1.3 尺寸效应的概率描述

描述某种材料断裂韧度的尺寸效应,传统的做法是取系列厚度试件做试验,每种厚度下至少作3个试样,取结果的平均值,再用式(1)、(2)对数据点进行拟合,得到韧度随厚度的变化曲线．该曲线可以直观地观察韧度变化趋势．传统方法在韧度值离散性小时,是合理的．当离散性较大,得到的曲线只能反映韧度值的大致变化趋势,用于韧度值预测时会产生很大的误差．

为了在离散性大的情况下,也能实现韧度值的有效预测,文中提出尺寸效应的概率描述方法．具体做法是:对每一厚度下的数据,计算得到δa、δb,再用δa和δb的数据分别按式(3)进行拟合,得到上下的两条曲线．两曲线的中间区域,即韧度值出现概率为P的区域．当韧度值离散性小时,此法得到一条窄带,与用均值拟合出的曲线近似;当离散性大时,得到一条宽带,P值设置越大,实验值落在其中的概率就越高．

2 试验验证

2.1 试验方法

采用20 ℃下,14MnNbq钢母材试件和16Mnq钢焊缝试件的实验数据[13],验证改进公式(3)的拟合性能．试验采用标准三点弯曲试件(尺寸比例如图2),共有5种厚度(10、14、22、30、40 mm),每种厚度下做3个试件．

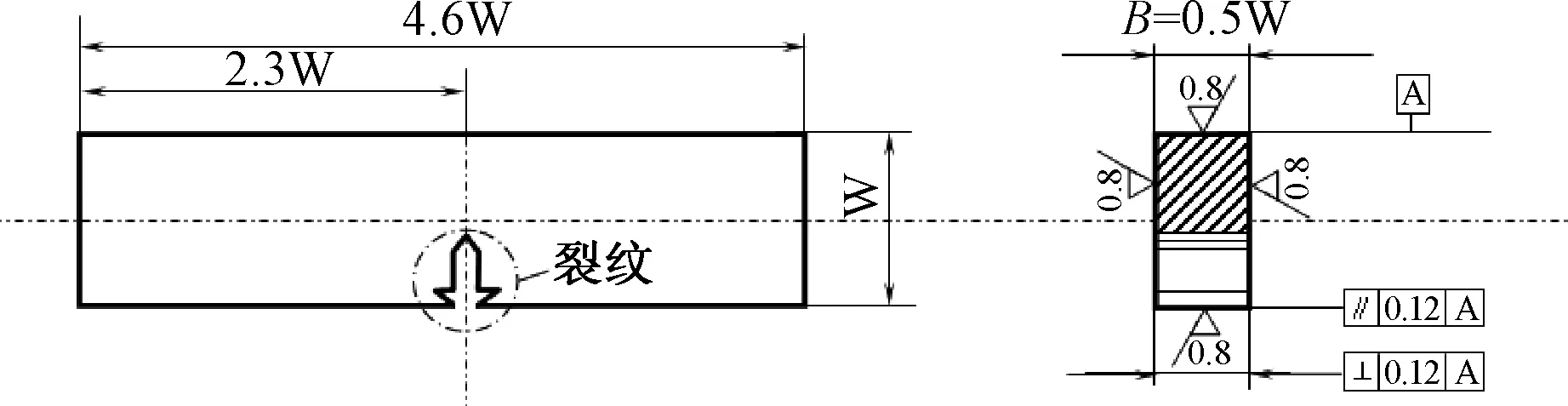
图2 三点弯曲试件尺寸图Fig.2 Dimensional drawing of three-point bending test piece

CTOD试验依照GB/T 2358-1994进行．试验前,在INSTRON1603高频疲劳试验机上预制疲劳裂纹,并保证初始裂纹总长占试样宽度的一半．主体试验在CSS2220万能试验机上进行,加载速度设为20 mm/min,当加载到最大荷载或着试件脆断时停机．试验结束后,用工具显微镜读取试件的初始裂纹长度a,在记录的P-V图中,读取最大荷载P和塑性位移分量VP．将a、P、VP和试件的尺寸代入规范所给公式,即可求出材料的CTOD值．

2.2 数据处理与曲线拟合

对每种材料,用δa、δb数据和均值数据分别按式(3)拟合曲线．拟合算法为最小二乘法,在Matlab平台上编程实现．拟合14MnNbq钢母材的数据时,只用10、14、30、40 mm处的值拟合曲线,22 mm处的值留下来验证改进公式预测韧度的准确性．拟合16Mnq钢焊缝的数据时,同样留下22 mm处的数据作验证．拟合得到的曲线如图3、4,拟合曲线在数据点处的误差见表1、2．

图3 14MnNbq钢母材试件拟合结果(20 ℃)Fig.3 Fitting results of 14MnNbq steel base metal specimens (20 ℃)

图4 16Mnq钢焊缝试件拟合结果(20 ℃)Fig.4 Fitting results of 16Mnq steel weld specimens (20 ℃)

从表1、表2看到,改进公式的拟合误差与预测误差均在10%以内．与原公式的最大拟合误差15.6%相比,拟合性能有明显提高,说明公式的改进方法有效．将改进公式用于两种不同材料的数据拟合,均得到良好的效果,说明新公式具有普适性．从两种材料在22 mm处的预测结果看到,改进公式在其适用的厚度范围内,韧度预测结果准确度较高．因此,在工程中用文中所提公式进行韧度预测,是一种能有效节省人力物力成本的切实可行的方法．

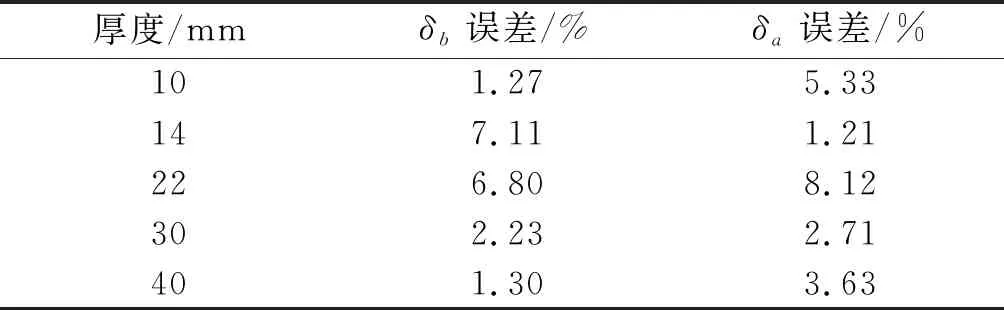
表1 14MnNbq钢母材试件拟合误差(20 ℃)Table 1 Fitting deviation of 14MnNbq steel base metal specimens (20 ℃)

表2 16Mnq钢焊缝试件拟合误差(20℃)Table 2 Fitting deviation of 16Mnq steel weld specimens (20 ℃)

3 结论

(1) 修改现有的CTOD尺寸效应公式,给出改进公式．新公式在描述14MnNbq钢母材试件和16Mnq钢焊缝试件的尺寸效应时,均表现出良好性能,表明改进方法合理且具有普适性．

(2) 通过K-S检验,证明了两种材料的CTOD值分布模型可用双参数威布尔分布描述．考虑断裂韧度值的离散性,用区间[δa,δb]表征其最有可能出现的范围,并提出了尺寸效应的概率描述方法．此法弥补了传统方法在断裂韧度离散性大时,韧度预测误差大的缺点．在工程应用中,求得一个韧度值可能存在的区间比均值更有意义．