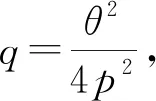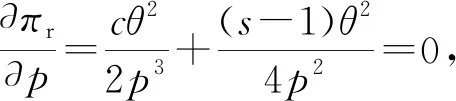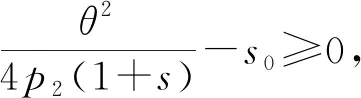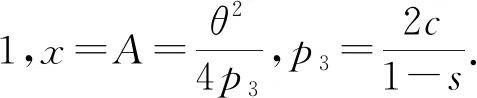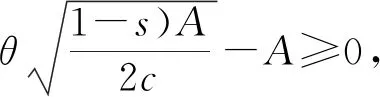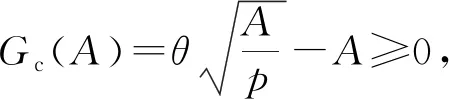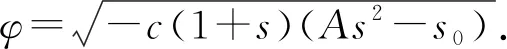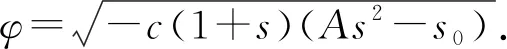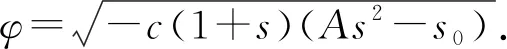B2C零售商配送定价策略对消费者购买行为的影响
吕丽莹,张 荣,刘 斌*
(1.上海海事大学 经济管理学院,上海 201306)(2.上海海事大学 物流研究中心,上海 201306)
近年来,随着互联网普及率的快速提高,网络购物正受到越来越多消费者的青睐.B2C电商的竞争日趋白热化,免运费成为重要的营销策略之一,频繁地被零售企业所使用.美国联合包裹最新研究表明,过半数受访者称曾将商品添加到购物车来获得免费投递的资格,有4/5的人为获得免运费而愿意为商品多等待两天时间[1].因此,越来越多的B2C零售商开始采取这种策略来吸引更多的消费者.例如,京东对不足39元的订单收取5元运费;当当网自2010年开始施行满29元免运费的策略;苏宁易购对单个订单满48元采取免运费策略.由于越来越多的B2C零售商采取免运费的配送策略,对于消费者来说,零售商的这种配送定价策略是否会对消费者的购买行为产生一定的影响?若有影响,那么在零售商采取不同水平的免运费时,消费者的购买行为和决策会发生哪些变化?文中将基于以上问题进行分析,探讨B2C环境下零售商制定不同配送定价策略时,对消费者购买行为决策的影响.
文献[2-4]中分别基于实证和数学模型研究的方式证明了网络零售商免运费策略对消费者的购买决策有一定影响.文献[5-7]中研究了在电商企业采取免运费策略下的零售商的订购决策,然而这些文献中免运费策略都是已经给定的,并没有涉及免运费策略的制定.文献[8]中在B2B环境下,研究了免运费策略的制定,其中,供应方先确定免运费阈值,然后零售商再决定购买数量.但上述模型仅是单纯对免运费条件下最优订购数量问题求解,其B2B的环境缺乏终端消费者的反应.文献[10]中研究了B2C零售商与消费者的博弈及B2C零售商面向多产品配送的免运费阈值决策问题,该研究虽然考虑到了消费者的反应及行为,但是针对的是B2C零售商自营配送的情况.此外,文献[11-12]均对电商零售商最优免运费阈值以及结合其他决策变量进行优化等问题作研究,但这些研究都是在假定运费价格给定的情况下,针对单一的电商零售商最优决策的研究.
综上,目前大多数文献仅限于研究B2B供应商或电商企业提供免运费政策对于零售商最优订购量决策的影响,而对于B2C环境下零售商的免运费政策的研究很少,同时也很少定性考虑在消费者行为基础上网络零售商的最优免运费策略.此外,大部分研究都已给定免运费水平,而未讨论在免运费水平不同时,消费者的购买行为会有怎样的变化.因此,文中通过对B2C零售商的配送定价策略进行分析,借鉴文献[5]中的研究,构建消费者效用函数,并建立消费者剩余模型,通过最大化消费者剩余来得到消费者在B2C零售商给定运费以及不同的免运费水平等条件下的购买决策.
1 模型假设及符号说明
1.1 模型背景及符号说明
在由一个B2C零售商及众多同类消费者构成的二级供应链中,消费者向B2C零售商下达一个购物订单,然后,B2C零售商向消费者提供订单配送服务,并根据消费者购物订单金额的大小,来确定是否享受免运费服务.免运费策略一般分为无条件免运费和有条件免运费.文中采取的运费收取模式是有条件免运费,即网上零售商对购买量在一定金额内的订单收取运输费用S,而对购买量超过一定金额的订单采取免运费的策略.在这样的模式中,B2C零售商设定一个免运费门槛,这会使得一部分网上消费者愿意通过凑单的方式来享受免运费服务,因此在一定程度上也能够提高B2C零售商的销售额,扩大销售规模,从而获得更大的利润.B2C零售商需要考虑到消费者对于产品的心理预期以及相应的购买行为,在保证其自身利润最大化的条件下确定最优的免运费值.
文中所用到的符号及含义如表1.

表1 消费者行为模型中的变量Table 1 Variables of the model of consumer′s behavior
1.2 模型假设
为了能更好研究消费者对于零售商变量(产品价格、免运费阈值、订单处理成本、运费)的反应程度,文中对模型做了假设:① 文中仅研究一个B2C销售商只销售一种单一产品的情况;② 供应链为由一个B2C零售商和一类消费者组成的二级供应链;③ 消费者是理性的,即消费者在自己消费能力允许的情况下,按照追求效用最大化原则进行消费;④ 为方便模型推导,假定消费者购买的数量为连续型变量;⑤ 运费是线性的,即由固定运费和可变运费两部分组成;⑥ 运费只与订单金额有关,与商品重量、数量等无关;⑦ 文中不考虑偏远地区配送费用增加的情况.
2 消费者行为模型
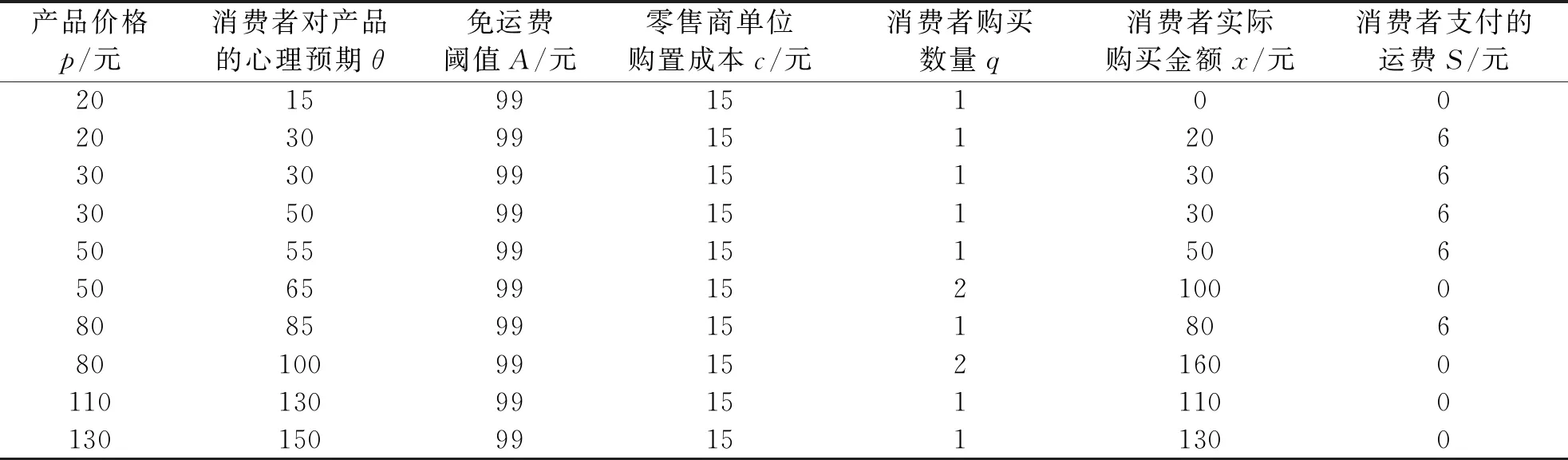
根据B2C零售商有条件免运费的规则,当消费者购买金额x 当x≥A时,消费者可以享受免运费的优惠,此时 零售商的利润为:πr=x-cq-S=pq-cq-(s0+spq) 证明:见附录1. 当x 证明:见附录2. 基于上一节消费者行为模型,对消费者在B2C零售商制定不同配送定价策略时的购买行为进行分析.上述求出的各种情况下的q*只是一个局部最优解,要真实反映消费者的最优购买数量,需要分情况进行讨论.同时,文中为了求解的方便,将q考虑成连续型变量. 命题1:当x (1) 当购买A所带来的消费者剩余小于购买p2q2所带来的消费者剩余,即 Gc(A) (2) 当购买A所带来的消 费者剩余大于等于购买p2q2所带来的消费者剩余,即 Gc(A)≥Gc(p2q2),并且Gc(A)>0时,消费者选择购买A; (3) 否则,消费者不会产生购买行为,即购买金额为 0. 证明:见附录3. 图1为在消费者购买金额x 图1 不同购买金额下消费者剩余曲线示意Fig.1 Consumer surplus curve diagram under different purchase amounts 根据上述分析,B2C零售商在采取不同配送定价策略时,对消费者购买行为决策的影响可以用以下命题表述. 命题2:当B2C零售商给定不同的免运费临界值A时,消费者的购买响应函数: (1) 当0≤A<4s0(1-s2)时, 证明:见附录4. 由命题2可以看出,消费者在电商平台的购买决策会受到B2C零售商所制定的免运费水平A的影响,具体表现为: (1) 若免运费水平A很小,即,0≤A<4s0(1-s2),则大多数消费者满足免运费条件;一部分对商品心理预期中等或较高而未达到免运费条件的消费者会选择增加其购买量至A,来享受免运费;但其他一些购买金额很小且对商品的心理预期较低的消费者会因为不愿支付运费,同时又不想购买更多的产品而放弃购买. 根据以上讨论,可以得出管理启示:免运费策略对于有较大金额订单的消费者更有吸引力.若一个消费者的购买金额很大,但仍小于免运费水平时,该消费者有可能会提高自己的购买金额,使其达到免运费水平A,来享受免运费服务.因此,电商零售商应该充分利用免运费策略来获取具有大金额订单的消费者. 为了验证上述理论,文中以京东商城中非生鲜产品的运费政策为例,通过算例分析模拟消费者的购买行为. 根据京东商城非生鲜产品的运费政策,同时为了计算的便利性,将京东商城的运费政策概括为:对订单金额<99元的消费者收取6元运费;订单金额>99元的消费者可享受免运费服务.同时,根据调研可得出如今大多数电商的购置成本约为15~25元,文中选取15元/单的单位购置成本,同时选取消费者购买金额x、产品价格p、消费者对于产品的心理预期θ、免运费阈值A、运费S等因素,消费者的订单情况和购买行为如表2. 表2 消费者购买行为与各变量之间的关系Table 2 Relationship between customers′ purchasing behavior and some variables related 根据上述表格可以得出以下结论: (1) 当消费者对产品的心理预期很低,或低于产品本身价格,同时免运费阈值较高时,消费者可能会因此而放弃购买该产品. (2) 当消费者对于产品的心理预期高于产品本身价格,而免运费阈值远高于商品价格时,部分消费者并不会为了享受免运费服务而增加其购买量,此时消费者会承担因购买产品而产生的运费. (3) 当消费者所购买的产品价格与免运费阈值较为接近但仍低于免运费阈值时,消费者会根据自己对于产品的心理预期等因素做出决策.若消费者认为产品价格满足自身的心理预期,同时对于运费的敏感度较高时,则很有可能会增加其购买量至免运费水平;而若消费者对于运费不敏感或敏感度较低时,则有可能坚持自己原来的购买方案,不会因为免运费服务而增加其购买量. (4) 对于订单金额原本已高于免运费阈值的消费者,无论其对于运费的敏感度如何,都享受免运费服务,因此这部分消费者也会按照原本的购买方案订购产品. 文中通过引入消费者效用函数,建立了消费者剩余模型.通过最大化消费者剩余,得出消费者在B2C零售商给定运费及不同免运费水平等条件下的购买决策,得到了符合直观认识的命题.研究结果表明: (1) 零售商的配送定价策略会对消费者的购买决策行为产生高于数量折扣等促销手段的影响; (2) B2C零售商在采取不同的免运费水平时,消费者会根据自己对商品不同的心理预期做出不同的购买决策. 文中仅讨论了B2C零售商采取不同配送定价策略对消费者购买行为影响的理论模型,没有进行实证调研.这将在以后进行研究,以佐证文中结论的正确性.在此基础上,将进一步研究消费者在确定了自己购买量之后,零售商在每种配送定价策略下所应制定的最优免运费水平的相关问题. 附录1引理1证明 零售商此时的收益为: 附录2:引理2证明 (1) 若消费者不增加其购买量至A,则 πr(q2)=p2×q2-cq2=p2q2-cq2 令Gc(p2q2)对q2求一阶导及二阶导,可得: 因此,Gc(p2q2)为q2的凹函数. 则消费者的购买金额为: 消费者的净剩余为: 零售商此时的收益为: (2) 若消费者增加其购买量至A,则享受免运费政策,此时: 附录3:命题1证明 比较Gc(A)和Gc(p2q2)的大小即可,消费者因为会选择使其净剩余最大的购买方式来进行其购买行为.当Gc(A)≥Gc(p2q2),同时净剩余Gc(A)>0时,消费者会选择增加其购买金额至免运费水平A;当Gc(A) 附录4:命题2证明 消费者需要通过比较Gc(A)和Gc(p2q2)的大小,使得消费者净剩余最大,来决定此情况下消费者的最优购买决策. 计算整理可得: 因此,当消费者的购买金额为A时,θ满足如下不等式: 求解上述不等式得到,当消费者购买金额为A时,θ要满足如下条件: 同时,为了保证消费者在购买金额为p2q2时,消费者剩余大于0,令 因此,当消费者购买量为pq时,θ要满足如下不等式: 求解上述不等式得到,当消费者购买金额为p2q2时,要满足: (3) 当消费者购买者放弃购买时,θ要满足如下不等式: 或 求解上述不等式得到,当消费者购买金额为0时,要满足: 或 综上所述,在x (1) 当0≤A<4s0(1-s2)时, 综合x≥A的情况,即可得到命题2的结论.2.1 消费者购买金额大于等于免运费临界水平

2.2 消费者购买金额小于免运费临界水平
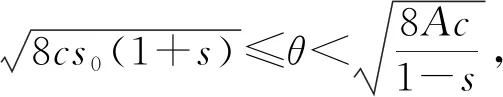
3 消费者购买行为分析



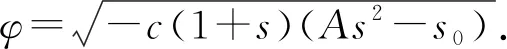

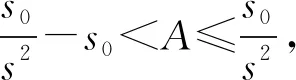
4 算例分析
5 结论