浅析极值点偏移四种题型的解法

江西省南昌市豫章中学 (330006)

王 鉴

根据近几年高考中的极值点偏移问题的题型，本人总结出了极值点偏移众多类型中的四种类型：无参零点和、有参零点和、有参零点积、有参零点商的题型及其可行的解题思路.

一、无参零点和

例1 已知函数f(x)=xe-x，若x1≠x2，有f(x1)=f(x2)，证明：x1+x2>2.

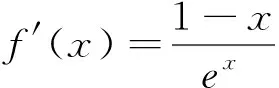
由x<1，则2x-2<0，即e2x-2<1，所以F′(x)>0,即F(x)在x<1时单调递增.而F(1)=0，所以f(x)2.

此题是最基本的题型,由此题的解答过程，可得到解决这类题型的四个步骤：(1)求解原函数的单调性；(2)利用分析法反推，把自变量的大小关系转化为函数的大小关系；(3)利用得出的函数大小关系构造新函数；(4)对新函数进行求导，利用其单调性以及函数取值的上或下界限即可证.

二、有参零点和

例2 已知f(x)=(x-2)ex+a(x-1)2有两个零点x1,x2，证明x1+x2<2.

证明：由题意可知x1,x2是方程(x-2)ex+

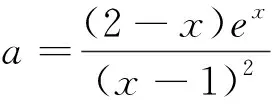
构造函数F(x)=g(x)-g(2-x)(x<1)，对函数求导，得到F′(x)<0,即F(x)在x<1时单调递减.而F(1)=0，所以g(x)>g(2-x)，所以g(x1)>g(2-x1).从而得证x1+x2<2.

此题包含了参数的问题，处理方法是把参数分离，利用同解方程的原理重新构造一个函数，其目的是让函数在求导时不被参数的范围困扰.而其具体步骤也是按第一个问题的方式来求解.

三、有参零点积

例3 已知f(x)=lnx-ax，若x1,x2是f(x)=0的两个根，证明x1x2>e2.

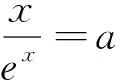
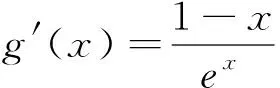
在此题的解答过程中，比前两题多了一个步骤，就是转化.我们把“零点积”问题转化为“零点和”问题，而这种转化利用了对数，因为只有对数在对待“积”的问题时，可以变成“和”的问题.当然这种转化需要重新构建方程，不能再用原方程.而一旦转化成“零点和”问题，那么求解的方法就和第二题是一样的.也就是说我们可以采用分离参数的方法把原函数改写，让参数在求导的过程中被消掉.

这时，我们总结步骤就发现由前两种类型的四步变成了五步：(1)把证明目标转化为x1+x2的形式；(2)求解原函数的单调性；(3)利用分析法反推，把自变量的大小关系转化为函数的大小关系；(4)利用得出的函数大小关系构造新函数；(5)对新函数进行求导，利用其单调性以及函数取值的上或下界限即可证.

四、有参零点商

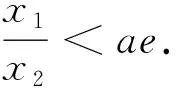
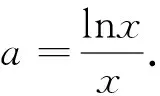
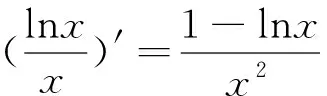
此题难度较大，其难度就体现在如何将“零点商”转化为“零点和”.它是利用对称性构造函数，通过函数因变量的关系反推自变量的关系，前三道例题的方法是通过自变量关系推因变量关系，利用推出的因变量关系构造函数；但这题是反过来的，先构造函数，然后通过因变量关系配合单调性反推自变量关系，从而把“零点商”问题转化为“零点和”问题.而最后步骤也不一样，此题最后是利用两个自变量的范围配合不等式的性质最终得出结论.

综合以上四道例题可以看出，上述四种类型中的第一种和第二种最重要，其它类型基本最终都可以化归为第一种和第二种类型，也就是说“零点和”问题是解决此种题目的关键.