我命我超纲,你用你高明——对用高等数学知识解答高考题的一点反思

江西省南昌市第三中学 (330047)

张金生

在高考中能否用“洛必达法则”、“拉格朗日中值定理”等高等数学知识答题?会不会扣分?一直是中学一线教师关心的问题,2015年江西省恢复考全国卷,在高考阅卷工作快结束时,全国卷命题专家到省考试院和中学阅卷教师代表座谈,关于能否用高等数学知识解答高考试题,专家用“我命我超纲,你用你高明”作答.2010年使用全国卷的某省在高考阅卷中，第21题中的第(2)问起初的评分标准是使用洛必达法则即使结果正确也要扣一分，试评结束后经过题长和顾问的讨论，决定不扣分.扣或不扣都有道理，但最终只会有一个确定的标准，所以使用超纲知识有时有一定风险.

2010年和2011年高考中的全国新课标卷中的第21题中的第(2)问，由不等式恒成立来求参数的取值范围问题，分析难度大，但用洛必达法则来处理却可达到事半功倍的效果.

例1 (2010年全国新课标理21题)设函数f(x)=ex-1-x-ax2.(1)若a=0，求f(x)的单调区间；(2)若当x≥0时f(x)≥0，求a的取值范围.

原解在处理第(2)问时的解法考生较难想到，现利用洛必达法则处理如下：

另解:(2)当x=0时，f(x)=0，对任意实数a,满足f(x)≥0；

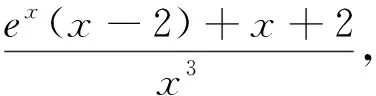
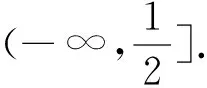
图1

对于阅卷过程中发现的这种应用高等数学空间解析几何的解法,还是给予了肯定.

根据试评结果，该题在制定评分细则时给出4种参考解法，其中一种是使用“对数平均值不等式”作答.

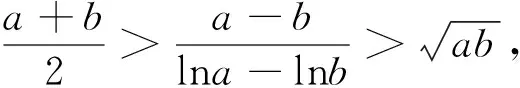
2018年高考《考试大纲》和《考试说明》里，进一步完善了对“一体四层四翼”高考评价体系的表述，将“立德树人、服务选才、引导教学”作为高考的核心功能，重申“必备知识、关键能力、学科素养、核心价值”四个层次的考查内容和“基础性、综合性、应用性、创新性”四个方面的考查要求.突出对“学习潜能”的考查.大学教授们命制高考试题，高等数学知识已经渗透到高考命题当中,它将高等数学的定义、定理用初等数学知识表述出来，即试题的设计来源于高等数学知识，但解决问题时是利用初等数学知识.这样，不仅显示出命题的立意新、情景新、思维价值高，而且拓宽了考生的视野，为考生进入高校学习新知识作了前期的准备，符合考纲对高考试题命题的创新要求，还可以借此来有效地提高考生的数学应用能力和数学核心素养，培养学生良好的数学思维品质和创新意识，同时也拓宽了试题命制的模式化.

高中阶段时间是很短的(两年多时间学完课程近一年时间复习)，对于那些非超常的普通学生，尤其是那些连高中数学基础题、中档题都做不好的学生，不去扎扎实实地学好高中教材内容，不切实际地好高骛远，利用宝贵的一点点课余时间去学习高等数学，试图通过学习高数(或奥数)，来提高高考成绩，得不偿失，“远水不能解近渴”，它不能解决高中数学中诸多的“挖地三尺”或“弯弯绕”的试题.但对极少数的顶尖的中学生，他们很早就接触了高等数学(或奥数)，并在高等数学(或奥数)的滋润下盛开数学之花，在高考中应用高等数学知识快速解答取得佳绩.对教超常学生的重点班的教师，站在高数背景下讲解数学考题，势必会有一种高屋建瓴之气势，对于学生开拓视野，提升能力也极为有用.“不登高山，不知天之高也；不临深谷，不知地之厚也”.