两个不等式的应用举例*

江苏省南京市金陵中学 (210005)

于 健 徐美松

含指数式和对数式的常见的两个不等式分别为ex≥x+1(x∈R)①，lnx≤x-1(x>0)②．

上述结论可以通过构造函数f(x)=ex-x-1和g(x)=lnx-x+1，利用导数求它们的最值加以证明．从几何的角度来看，直线y=x+1和y=x-1分别是曲线y=ex在(0,1)处、y=lnx在(1，0)处的切线；由不等关系可知y=x+1的图像恒在y=ex的图像的下方(除去切点)，y=x-1的图像恒在y=lnx的图像的上方(除去切点)．(①、②被形象称为切线不等式)

在理解和记忆的基础上，运用这两不等式进行适当放缩，可以将含有复杂的指数式、对数式的求值证明问题转化为简单的有理式(整式、分式)的求值证明问题，进而将问题破解．

一、适时转化 变繁为简

例1 (2013年新课标卷)已知函数f(x)=ex-ln(x+m)．当m≤2时，证明f(x)≥0．

简证：利用两个结论ex≥x+1，lnx≤x-1得，f(x)=ex-ln(x+m)≥(x+1)-[(x+m)-1]=2-m≥0．

例2 (2013年清华大学等“华约”自主招生考试)已知f(x)=(1-x)ex-1．

(1)求证：当x>0时，f(x)<0；

(2)若数列{xn}满足xne=e-1，x1=1，求证：{xn}递减．

(2)欲证{xn}递减，只要证xn>xn+1(xN+)，即证exn>exn+1,即欲证xnexn>xnexn+1=exn-1，只要证f(xn)=(1-xn)exn-1<0(xN+)，又由(1)知x>0时，f(x)<0，故证xn>0(xN+)．

当n=1时，x1=1>0，假设当n=k时，xn>0正确，即xk>0；

又xkexk+1=exk-1>(xk+1)-1=xk，则exk+1>1，则xk+1>0，所以当n=k+1时，xn>0也正确．所以xn>0(xN+)成立，数列{xn}递减．

总结:例题1、2都联系了不等式ex≥x+1，lnx≤x-1，再由代换思想得eg(x)≥g(x)+1，lng(x)≤g(x)-1．如ln(x+m)≤(x+m)-1，exk>xk+1．在例2第(2)小题长链条、多环节的解题过程中，解题者往往会有“山重水复疑无路”之感，当再次嵌用了不等式

exk>xk+1，顿时“柳暗花明又一村”．

二、深度转化 以静制动

例3 (2013江苏高考)设函数f(x)=lnx-ax，g(x)=ex-ax，其中a为实数．

(1)若f(x)在(1，+∞)上是单调减函数，且g(x)在(1，+∞)上有最小值，求a的取值范围；

(2)若g(x)在(-1，+∞)上是单调增函数，试求f(x)的零点个数，并证明你的结论．

解:(1)略；

(ⅰ)当a≤0时，f(x)=lnx-ax在(0，+∞)上单调递增．

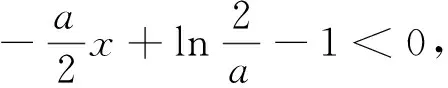
3）串口通信使用的MSComm控件，并非Visual Studio自带，而是VC++6.0的旧版本控件，虽然易于编程，但存在不便于软件发布等问题。

总结:关于零点的判断，解答时大多都是通过具体赋值来判断相应的函数值的符号，其中自变量的赋值往往和参数有关，也正是因为这一点，还需要对函数值的符号加以证明，而如何赋值往往没有头绪．

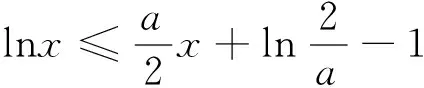
例4 (2014福建高考)已知函数f(x)=ex-ax(a为常数)的图像与y轴交于点A，曲线y=f(x)在点A处的切线斜率为-1．

(1)求a的值及函数f(x)的极值；

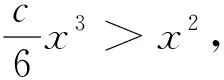
(2)证明：当x>0时，x2

(3)证明：对任意给定的正数c，总存在x0，使得当x∈(x0,+∞)，恒有x2

解:(1)略；(2)略；

(3)的证明：(方法一)不妨令x>0，则x2

令c′=lnc，上述问题转化为：

对任意给定的实数c′，存在x0≥0，使得当x∈(x0，+∞)时，2lnx

记h″(x)为h′(x)的导函数，h‴(x)为h″(x)的导函数．

例5 (无锡2015届上学期期末)设函数f(x)=x2lnx-ax2+b在点(x0，f(x0))处的切线方程为

y=-x+b．

(1)求实数a及x0的值；

解：(1)略；

令-x+b>0，则当00．

从以上所举例子中可以看到切线不等式在优化问题解答中所发挥的巨大作用，类似的例子在高考压轴题中还有很多，我们可以把切线不等式根据题目中的条件进行一系列的改造，这些派生的不等式在处理问题时会发生更大的作用.遵循本文给出的解题线索，读者可以研究还有更多的派生不等式及其应用.