大功率分数阶电感的电路实现

卢曰海，丘东元，张 波，陈艳峰

（华南理工大学电力学院，广州510640）

研究发现自然界中许多物理现象的本质都具有分数阶的特性[1-3]，如电感是电气工程领域中一个重要的电路元件，在以往的研究中通常被看作整数阶元件，然而整数阶电感并不存在，用分数阶模型来描述电感更为准确[4]。

分数阶电感的构造一直是学者们关心的问题，文献[5]提出了以磁流变流体为磁芯的类似于变压器的分数阶电感模型，但是这种模型构造复杂，不利于推广。目前分数阶电感的电路实现方法主要还是基于电阻、电感和运放等器件，常见的有采用RL链分抗[6-8]和跨导运算放大器[9]实现0 ～1阶的分数阶电感，基于广义阻抗转换GIC（general impedance converter）[10]电路实现1 ～2阶的分数阶电感。但是这些电路普遍具有如下缺点：①使用的器件较多，整个电路结构复杂；②当需要改变分数阶电感的感值或阶数时，整个电路的元件都要更换；③因采用了运算放大器等模拟器件，电路模型仅限于小功率场合的应用。

针对现有分数阶电感等效电路存在的缺点，本文提出了一种阶数和感值可调的大功率分数阶电感等效电路。首先介绍了分数阶电感的一些基本性质，然后阐述了大功率分数阶电感的构造原理，接着通过仿真和实验验证该模型的可行性，最后将本文提出的大功率分数阶电感运用到RLβC并联谐振电路中。

1 分数阶电感性质

将传统电感元件的电压、电流整数阶关系拓展到分数阶，可以得到分数阶电感元件的电压电流关系[11]，即

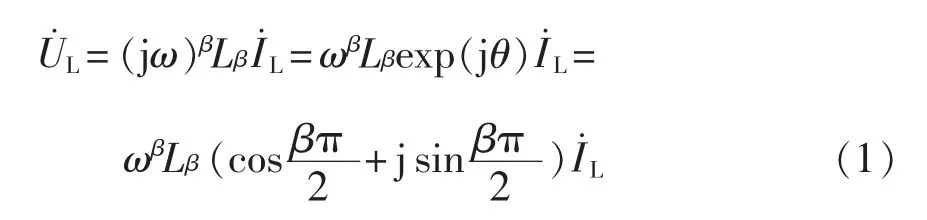
式中：β为分数阶电感的阶数；θ为分数阶电感的电压和电流的相位差，θ=βπ/2。

类似地，可以获得分数阶电容的电压电流关系式[11]，即

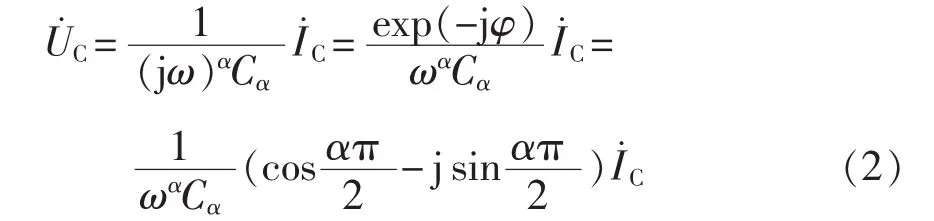
式中：α为分数阶电容的阶数；φ为分数阶电容的电压和电流的相位差，φ=απ/2。

分数阶电容和分数阶电感被统称为分数阶电抗元件。根据元件的电压电流关系，传统的整数阶电路元件（如电阻、电容和电感）和分数阶电抗元件的阻抗向量如图1所示。从图1可见，分数阶电感的特性则是介于电阻和传统的整数阶电感之间，而分数阶电容的特性是介于电阻和传统的整数阶电容之间。此外，分数阶电抗元件的电压电流相位差只和其阶数有关，改变分数阶电抗的阶数可以使其电压电流的相位差在（0～2π）整个相平面内变化[6]。整数阶电感和电容则可以看作是分数阶电抗元件的一个特例。

由式（1）可得分数阶电感的阻抗为

式中：ω为分数阶电感端电压或端电流的角频率；Lβ为分数阶电感；β为分数阶电感的阶数，0＜β＜2。当β=1时，分数阶电感为理想的整数阶电感。

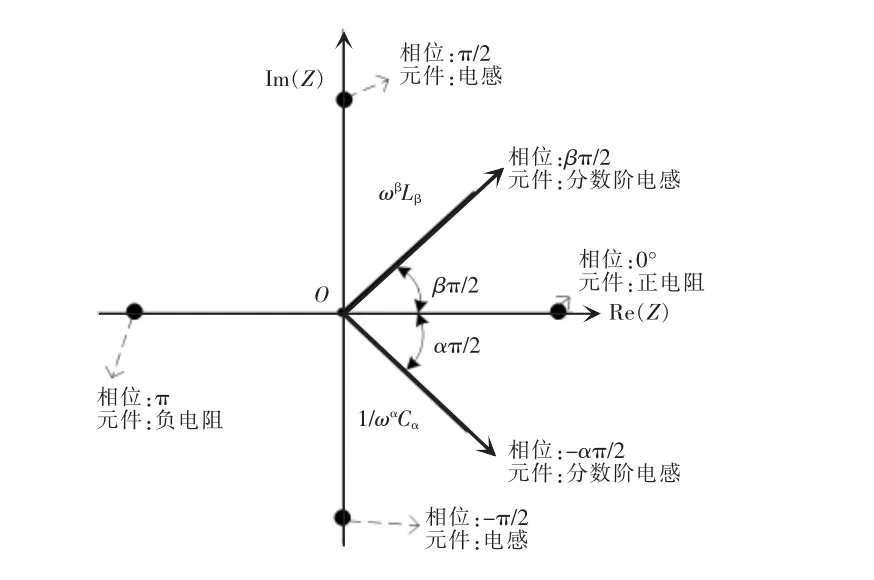
图1 整数阶电路元件和分数阶电抗元件的阻抗向量Fig.1 Impedance phasor diagram of integral-order circuit elements and fractional-order impedance elements

根据式（3），总结出分数阶电感的性质如下：

（1）分数阶电感的端电流和端电压呈β阶积分关系；

（2）分数阶电感的阻抗不再像传统整数阶电感那样只含有感性成分，而且还包含阻性成分。当分数阶电感的阶数 β＜1 时，其阻性成分，呈正阻性，此时分数阶电感为有损元件；当β>1时，其阻性成分，呈负阻性，此时分数阶电感为有源元件；

（3）分数阶电感的相角（θ=βπ/2）不随频率改变，只和分数阶电感的阶数相关，故分数阶电感也被称为常相位器件[13]。

2 大功率分数阶电感的电路模型

本文构造的大功率分数阶电感电路原理如图2所示，其中A、B为分数阶电感元件的两个端口，采用数字信号控制器控制的逆变器为受控电压源；UDC为直流电压源，Lf为滤波电感，Cf为滤波电容，ui（t）为逆变器的输出电压，uL(t)为分数阶电感等效电路两端的电压（又称为输入电压），iL(t)为流过分数阶电感等效电路的电流（又称为输入电流），R为与受控电压源串联的电阻，uM（t）为数字信号控制器输出的调制信号，Ka为感值调节系数，β为分数阶元件的阶数。大功率分数阶电感等效电路的构造思路如下：电压采样器采样输入电压，控制器根据所采集到的电压，并结合所设定的分数阶电感的阶数和感值要求，产生相应的控制信号，控制逆变器中开关管的开通和关断，从而控制逆变器的输出电压，最后使得整个电路的输入电压和输入电流呈现分数阶电感电压和电流的特性。

大功率分数阶电感电路具体实现过程如下：根据分数阶电感的电压和电流关系，在s域中输入电压和电流需满足

式中，UL（s）和 IL（s）分别为电压 uL（t）和电流 iL（t）的拉氏变换形式。

若分数阶电感等效电路的输入电压uL（t）和逆变器的输出电压ui（t）已知，由图2可得输入电流的表达式为

式中：R为与受控电压源串联的电阻；Ui（s）为电压ui（t）的拉氏变换形式。

结合式（4）和式（5），可得逆变器的输出电压为

由于逆变器输出电压ui（t）和数字信号控制器输出的调制信号uM（t）同相位，幅值成比例，可得数字信号控制器的输出为

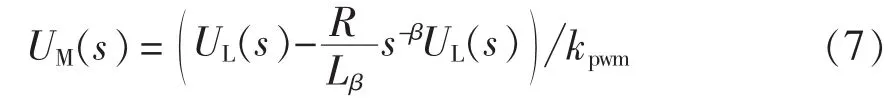
式中：UM（s）为电压 uM（t）的拉氏变换形式，kpwm为数字控制信号器电压采样系数的倒数。

图2 大功率分数阶电感电路原理Fig.2 Schematic of circuit for high-power fractional inductor

令 1/kpwm=KS为电压采样系数，R/Lβ=Ka，则进一步得到数字信号控制器的输出为

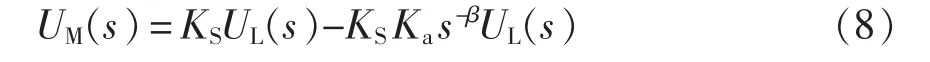
结合式（4）～式（7），可得分数阶电感电流为

假设输入电压为 uL（t）=ULsin（ωt），对应的 β阶积分运算结果[15,16]为

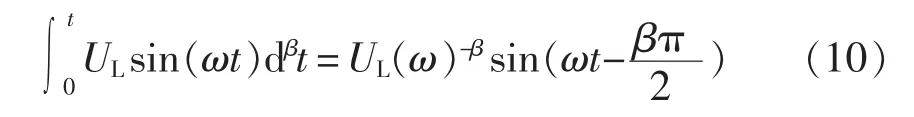
结合式（9）和式（10），此时分数阶电感电流为

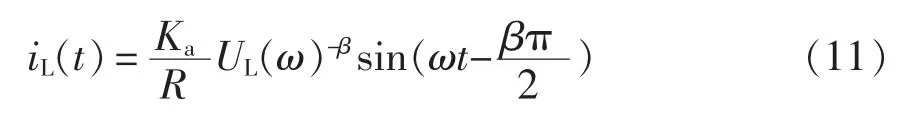
综合式（8）、式（10）和式（11），可得数字信号控制器的输出为

将式（12）展开，此时数字信号控制器的输出为

式中：uS（t）为采样电压，uS（t）=KSULsin（ωt）；K1=sin（πβ/2）；K2=cos（πβ/2）；K3=ω－β；Kd=1/ω。

若把调制信号 uM（t）的幅值控制在（0，1）范围内，根据式（13），可得到Ka的取值范围为

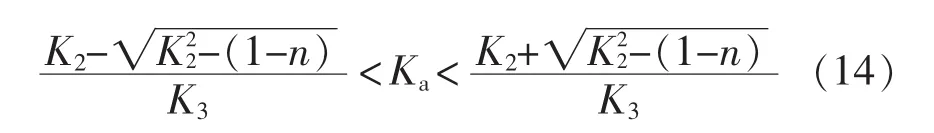
式中，n=1/（KSUL）2。

从上述推导结果可见，根据设定的阶数β，改变控制参数K1、K2和K3，可以实现不同阶数的分数阶电感构造。而改变Ka则可以实现不同感值的分数阶电感构造。因此，此模型可以很方便地构造出不同参数的分数阶电感，分数阶电感的阶数和感值调节非常灵活。

结合式（11）可得分数阶电感的有功功率为

可见，分数阶电感的功率与分数阶电感的感值、阶数以及输入电压紧密相关。采用不同的参数，分数阶电感的功率将不同。此外，从图2可知，分数阶电感的等效电路主要由逆变器和串联电阻R组成，而逆变器的类型以及所用的元器件可以根据应用场合的电压、电流或功率来确定。因此，本文所提出的分数阶电感电路实现方法可适用于各种不同的功率等级场合。

3 模型验证

根据上述分析，本文在仿真软件PSIM中搭建的大功率分数阶电感等效电路模型，如图3所示。其中，uS为采样电压，KS为采样系数。

采用4组不同的参数来验证所设计的大功率分数阶电感电路模型。其中：直流电源电压UDC=100 V，串联电阻R=100 Ω，三角载波幅值Utri=1 V，滤波电感Lf=1.5 mH，其他的参数如表1所示。根据式（11），理论上分数阶电感电流滞后电压的角度为θ=πβ/2，分数阶电感为 Lβ=R/Ka，根据式（15）算得 4组参数下的功率P。从表1可以看出，当分数阶电感的阶数小于1时，分数阶电感为有损元件；当阶数大于1时，分数阶电感为有源元件。

表1中4组数据对应的分数阶电感电压、电流仿真波形如图4所示。其中Δt为分数阶电感电压峰值和电流峰值的时间差，UL为分数阶电感电压的有效值，IL为分数阶电感电流的有效值。根据仿真结果，相应的分数阶电感电流滞后电压的角度θs和分数阶电感Lβs的计算方法为

图3 大功率分数阶电感等效电路模型Fig.3 Equivalent circuit model of high-power fractional inductor

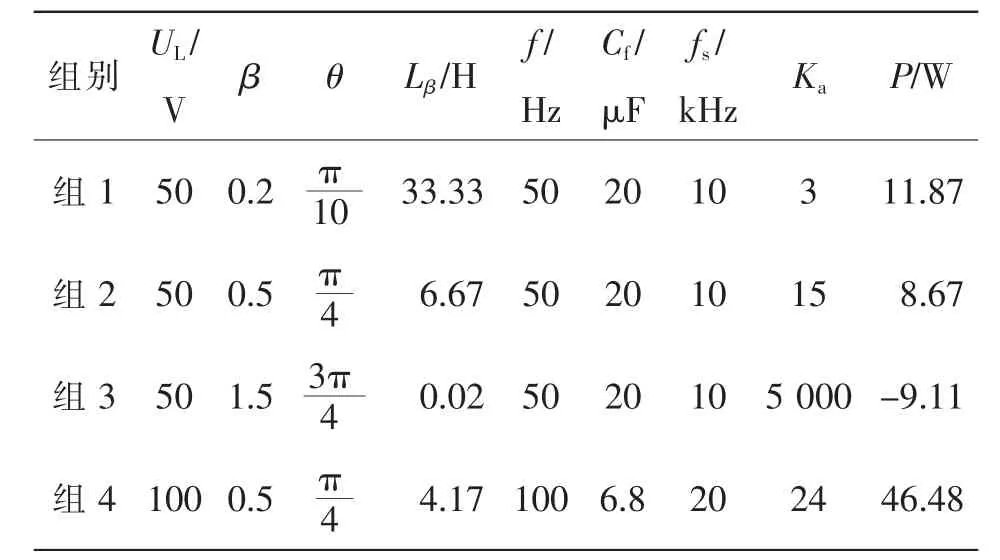
表1 大功率分数阶电感电路的参数Tab.1 Circuit parameters of high-power fractional inductor

图4 分数阶电感模型的电压、电流仿真波形Fig.4 Simulation waveforms of voltage and current of fractional inductor model

为了进一步验证该模型的正确性，本文搭建了大功率分数阶电感实验平台，如图5所示。其中，控制信号由DSP TMS320F28335产生，逆变器的开关管选用MOSFET IRF830，开关管对应的驱动选用光耦隔离芯片TLP250，其他实验参数与仿真参数相同。可以得到表1中4组参数的电压、电流实验波形如图6所示。根据图6中的实验波形，可以得到电压和电流的相位差θe以及电压、电流的有效值，并结合式（17）可得到相应的分数阶电感Lβe。

表2列出了4组不同分数阶电感参数所对应的相位差和感值的理论结果、仿真结果和实验结果。从表2中可以看出理论计算、仿真结果和实验结果都基本一致，从而验证了该模型的正确性。

图5 大功率分数阶电感实验平台Fig.5 Experimental platform of high-power fractional inductor

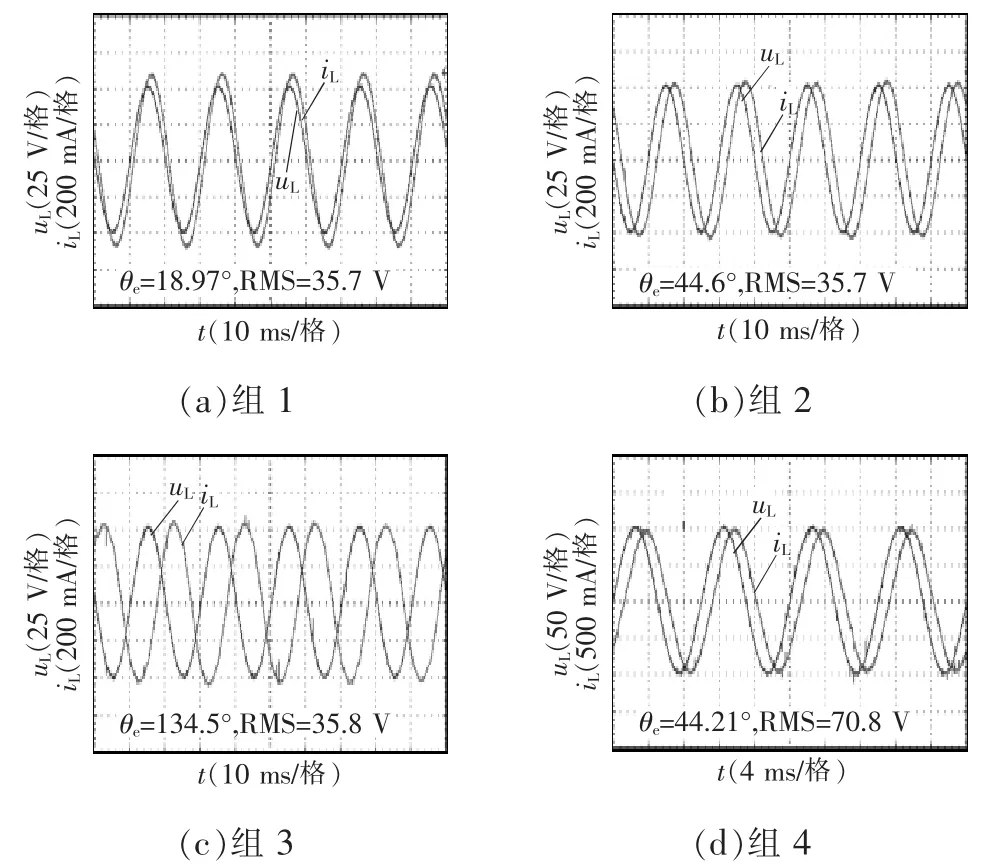
图6 分数阶电感的电压、电流实验波形Fig.6 Experimental waveforms of voltage and current of fractional inductor

表2 分数阶电感模型的理论计算、仿真结果和实验结果Tab.2 Calculation,simulation and experiment results of fractional inductor model

4 大功率分数阶电感在RLβC并联谐振的应用

传统RLC并联电路的谐振频率仅和电感L、电容C相关，若将分数阶电感替换传统的电感L，得到分数阶RLβC并联谐振电路如图7所示。

由图7可得分数阶RLβC并联电路的导纳为

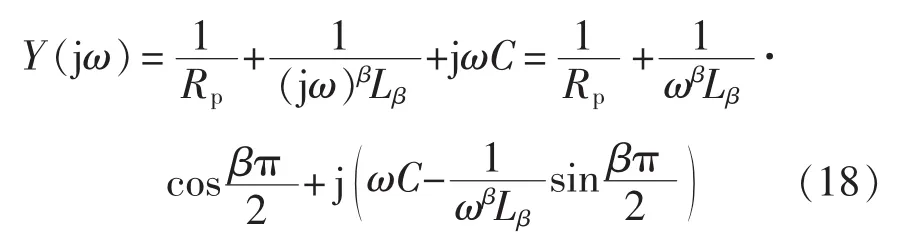
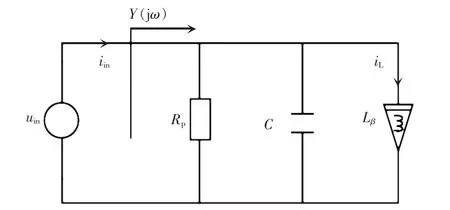
图7 分数阶RLβC并联谐振电路Fig.7 Fractional RLβC parallel resonant circuit

当导纳的虚部为0时，可得分数阶并联电路的谐振频率为

由式（19）可知分数阶并联谐振频率不仅和分数阶电感、电容有关，而且还与分数阶电感的阶数有关，故分数阶电感的引入会增加整个系统的设计自由度。

将构造的大功率分数阶电感运用到RLβC并联谐振电路中。设分数阶电感模型中UDC=100 V，R=100 Ω，Utri=1 V，Lf=1.5 mH，Cf=6.8 μF，并联电阻 Rp=100 Ω，C=4.5 μF，谐振频率为 ω=200π rad/s。

由式（19）可得满足RLβC并联谐振条件下分数阶电感和阶数的关系，如图8所示。已知阶数β>1时，分数阶电感为有源元件，故在设计时可令分数阶电感的阶数β>1。从图8中可知，当β>1时，随着阶数的增加，实现并联谐振所需要的感值减小。

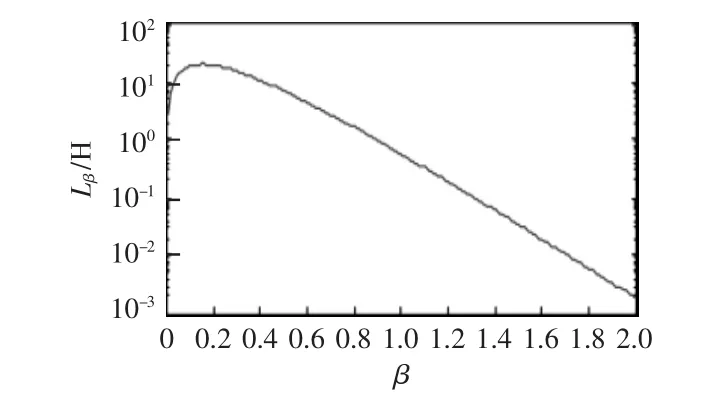
图8 RLβC并联谐振下分数阶电感和阶数关系曲线Fig.8 Curve of inductance vs order of fractional inductor under RLβC parallel resonance

当分数阶电感的阶数为β=1.4，由式（19）可得分数阶电感为Lβ=34.6 mH；当分数阶电感的阶数为β=1.5，则相应的分数阶电感为Lβ=15.8 mH。若输入电压uin=50 sin（200πt），可以得到不同阶数 β下并联谐振电路的输入电压、输入电流和分数阶电感电流的仿真与实验波形，如图9所示。从图9中可知，2组参数下输入电压和输入电流均同相位，意味着整个RLβC并联电路处于谐振状态，各电量的实验结果和仿真结果基本一致，从而验证了分数阶电感的引入可增加整个RLβC并联谐振电路的设计自由度以及该大功率分数阶电感运用在谐振电路的可行性。

图9 RLβC并联谐振电路的仿真和实验波形Fig.9 Simulation and experimental waveforms of RLβC parallel resonant circuit

5 结论

针对现有的分数阶电感等效电路存在的缺点，本文提出了一种大功率分数阶电感等效电路，并通过仿真和实验验证了该模型的正确性。所构造的大功率分数阶电感具有以下特点：

（1）大功率分数阶电感的阶数调节范围为0 ～2；

（2）改变数字控制器的参数可实现分数阶电感阶数和感值的灵活调节；

（3）该等效电路的功率等级可视实际应用场合而定，为分数阶电感在大功率场合提供了参考。

本文将构造的大功率分数阶电感成功地应用到并联谐振电路中，进一步说明了所提大功率分数阶电感电路模型的可行性。