变压器绝缘故障类型的改进型RBF神经网络识别算法

李 浩，王福忠，王 锐

（河南理工大学电气工程与自动化学院，焦作454000）

电力变压器作为电力系统中的关键设备，承担着电压变换和电能分配与传输的任务，其运行可靠性直接关系到系统的供电安全与稳定运行[1,2]。电力变压器内部潜伏性绝缘故障在变压器故障类中占有相当的比重，因此研究其内部潜在绝缘故障诊断方法具有重要意义。变压器油气组分分析DGA（dissolved gas analysis）技术作为诊断其内部潜在绝缘故障的方法之一，能够及时有效地发现变压器内部潜伏性绝缘故障及其发展程度，以防止由此引发的安全事故[3]。传统的三比值法及其改良方法在工程中虽多有应用，但该类算法只能粗略诊断故障类而无法准确诊断具体故障。目前，为准确诊断变压器内部潜在绝缘故障及提高诊断准确率，国内外学者引入了多类智能算法包括人工神经网络[4-9]、人工免疫算法[10]、支持向量机[11-12]等。

径向基函数 RBF（radial basis function）神经网络算法以其收敛速度快、函数逼近能力强等优点，近年来被广泛应用于模式识别、故障诊断等领域。但如何构造一个最优的、合理的RBF神经网络结构一直以来都是一个难点[13]。文献[14]采用RBF神经网络进行变压器故障诊断，为了解决网络结构复杂、训练时间长等问题，利用粗糙集原理对训练数据进行挖掘，精简了网络结构提高网络训练速度；文献[15]采用免疫蚂蚁算法对训练数据进行处理，优化RBF网络隐层参数，并利用最小二乘算法计算RBF网络输出权重，提高了网络的泛化能力与收敛速度。

本文提出一种改进的RBF神经网络故障诊断算法，针对变压器内部潜在的具体绝缘故障建立故障诊断模型，并分别以人工免疫网络算法与粒子群优化算法对诊断模型的中心及权重寻优以达到精简网络、提高网络泛化能力和收敛速度的效果。仿真实验结果表明，该方法能有效地识别变压器内部潜在绝缘故障类型，提高诊断准确率。

1 变压器内部潜在绝缘故障类型及其油气成分

电力变压器内部绝缘系统常由两类基本绝缘材料构成：固体材料（层压纸板、绝缘纸等）和液体材料（变压器油）。当变压器内部发生或者存在潜伏性故障时，其固液材料会在电、热等多因素作用下分解产生某些特定气体并溶于变压器油中，表1为常见变压器内部潜在绝缘故障类型及其油气成分。

由表1看出，从性质上可将电力变压器内部潜在绝缘故障划分为热性与电性故障两大类，热性故障与电性故障各有4类，共8类故障。不同的故障类型所产生的氢气（H2）、甲烷（CH4）、乙烷（C2H6）、乙烯（C2H4）、乙炔（C2H2）、一氧化碳（CO）和二氧化碳（CO2）等气体不同。为此，本文以表1中所列的8种具体故障类型与发生故障类时的7种气体的产气特点为依据，对电力变压器的内部潜在绝缘故障进行诊断，其中，以x1～x7代表7种特征气体含量，以y1～y8代表表1中8类具体的内部潜在绝缘故障。

表1 不同故障类型产生的气体成分Tab.1 Gas production types under different types of fault

2 基于RBF神经网络的变压器故障诊断模型

2.1 变压器内部潜在绝缘故障诊断模型的结构原理

RBF神经网络是一种生物背景很强的前馈型神经网络，具有较强的函数逼近能力[16]。该神经网络的每个隐含层神经元传递函数都构成了拟合平面的一个基函数，是一种局部逼近网络即对于输入空间的某个局部区域只存在少数的神经元用于决定网络的输出。由于该网络学习速度快，函数逼近能力较强，被广泛应用于函数逼近、故障诊断等领域，为此本文以RBF神经网络原理建立如图1所示的变压器内部潜在绝缘故障诊断模型。

该模型主要由输入层、隐含层和输出层组成。其中，输入层由一些感知单元组成，它们将网络与外界环境连接起来，本文表示变压器的7种特征气体量；第2层是网络中仅有的一个隐层，它的作用是从输入空间到隐空间之间进行非线性变换；输出层是线性的,它为作用于输入层的激活模式提供响应，本文中表示8种变压器潜在绝缘故障。网络隐层的非线性作用过程对网络输出起着至关重要的作用，隐层基函数形式表示为

式中：sj为隐层第 j个神经元的输出；φj（·）为基函数；cj为隐含层基函数的中心矢量；||x-cj||为输入量x与基函数中心矢量cj间的欧式距离；a为隐层神经元数。

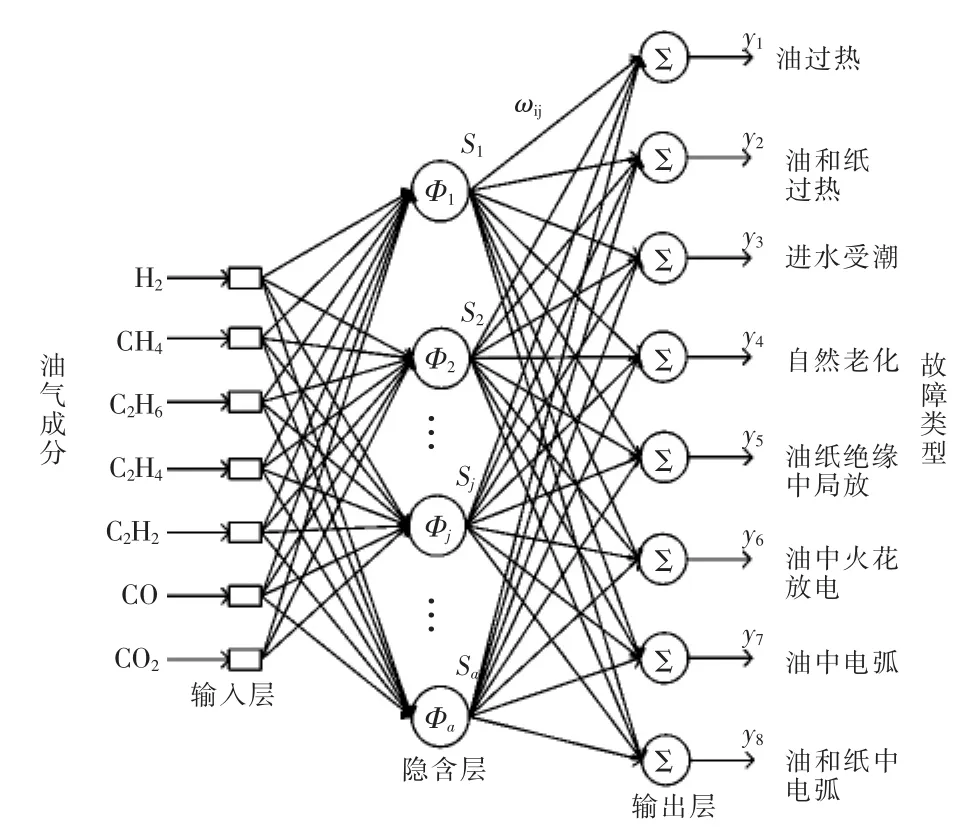
图1 RBF神经网络故障诊断模型Fig.1 Fault diagnosis model of RBF neural network

高斯径向基函数由于具有形式简单、解析性好等优点而成为最常用的径向基函数，其基本形式为

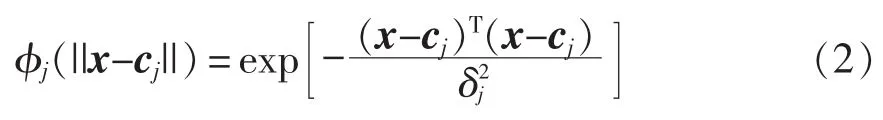
网络隐含层到输出层实现线性映射，网络输出层为隐含层节点的线性组合，其表达式为

式中：yk为输出层节点k的输出；m为输出层层数。

2.2 故障诊断模型输入输出设计

现假设本文共收集N组样本数据记为X=[x1，x2，…，xN]，其中的任意一组元素 xi=[xi1，xi2，xi3，xi4，xi5，xi6，xi7]T代表一组故障数据，同该组数据相对应的网络实际输出记为 Y=[yi1，yi2，yi3，yi4，yi5，yi6，yi7，yi8]T。由于隐含层与输出层为线性映射关系，因此根据模型结构原理可得到输出层结果表达式为

式中：ωk为输出层节点k的权值矢量，ωk=[wk1,wk2,…,wka]T；Φ 为基函数矢量，Φ=[φ1,φ2,…，φa]T。

对式（4）分析可知，构建RBF神经网络故障诊断模型的关键在于求取网络隐含层中心与隐含层到输出层权重。详细阐述如下。

2.3 基于免疫网络算法的诊断模型隐层中心的确定

理论上，RBF网络模型中心应覆盖整个输入空间，中心数目过多会导致网络计算量增加，而中心数目过少则无法反映输入空间的特点，两者均会影响网络的泛化能力。人工免疫网络算法作为一种新型智能算法，它通过模拟抗原与抗体之间作用关系，使抗体在学习抗原模式过程中被不断优化，从而得到能够反映抗原特性的特殊抗体[17-19]。因此，本文以人工免疫网络算法对输入模型的故障样本进行处理以求得隐层中心，处理算法如下。

（1）原始抗原集选取。选取变压器发生内部绝缘故障时产生的7种特征气体含量所构成的向量xi=[xi1，xi2，xi3，xi4，xi5，xi6，xi7]为原始抗原集，其中 xi1～xi7分别代表7种特征气体含量。

（2）气体特征向量归一化。本文采用浓度归一法将特征气体向量归一化[20,21]，设归一化前的量记为 xi=[xi1，xi2，xi3，xi4，xi5，xi6，xi7]，归 一化 后 的量记 为x'i=[x'i1，x'i2，x'i3，x'i4，x'i5，x'i6，x'i7]，归一化公式为

（3）气体特征量净化。为除去气体特征量中的相似个体，需对归一化后的气体特征量进行净化。个体间的相似程度常由欧式距离来表征，因此变压器气体特征量的净化是以抗原、抗体间的欧式距离大小cv为标准进行的，通常当cv小于0.01时，表示两者相似，其中一个个体需被删除。n维空间的欧氏距离为

（4）抗体集合初始化。随机抽取N组包含各故障类型的样本作为免疫网络的初始抗体集Ab；

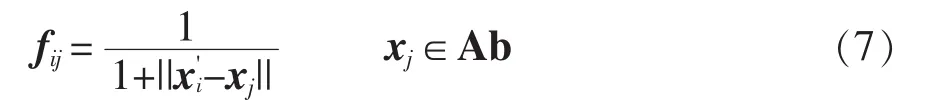
（6）克隆选择。以亲和度向量fi为依据，从抗体集合Ab中选取n个亲和度最高的抗体组成新的抗体集合Ab{n}；

（7）克隆操作。对新抗体集合Ab{n}中的抗体进行克隆操作，克隆数目Nc表示为

式中：round（）为取整操作；Kscale为克隆规模。经克隆操作后的抗体集记为Ci。

（8）变异操作。对克隆后的抗体集Ci进行变异操作得到，其变异操作公式为

式中，α为学习速率，由亲和度决定，亲和度越大α越大。

（10）免疫抑制操作。计算抗体集Ab*中各个抗体之间的亲和度，删除亲和力大于特定阈值σs的抗体，更新抗体集Ab*；

（11）迭代。重复上述操作直到达到规定的迭代次数为止。

2.4 RBF网络诊断模型权重的粒子群优化算法

粒子群优化 PSO（particle swarm optimization）算法作为一种新型优化算法近年来在函数寻优、神经网络优化等领域多有应用[22-23]。同其他优化算法如遗传算法GA（genetic algorithm）等相比，无交叉、变异等过程，因而简单且易实现，本文选用PSO算法对诊断模型的连接权重进行寻优。

PSO算法以P-V模型寻优搜索，每个粒子代表解空间中的一个潜在解。假设m个粒子组成的群体在R维解空间中飞行，每个粒子由它的位置和速度向量表示，记为 Pi=（Pi1,Pi2,…，PiR）、Vi=（Vi1,Vi2,…，ViR）。每次迭代中个体搜索到的最优值记为BestPi，群体搜索到的最优值记为BestGi，每个粒子的速度和位置的变化公式为

式中：i=1,2,…，m；d=1,2,…，R；k 为迭代次数；ω 为惯性因子；BestPid、BestGid为粒子i在第k次迭代中个体极值与群体极值的位置坐标；C1、C2为学习因子；R1、R2为[0,1]间的随机数。

以PSO算法寻求故障诊断模型的最佳连接权重，随机产生多个粒子以构成粒子群，群体中每个粒子的位置向量设为RBF网络的一组权重。在以PSO算法寻优搜索时，当目标函数值达到最小时，即可求得网络的最佳权重。其寻优算法步骤如下。

步骤 1粒子群初始化。设定学习因子C1、C2及最大迭代次数kmax，确定粒子的个数m，随机产生粒子的位置向量Pi和速度向量Vi；

步骤2计算适应值。以RBF网络故障诊断模型的输出结果来计算每个粒子的适应值，记录个体粒子的极值及群体粒子的极值分别用BestP和BestG来表示。寻优过程的适应值评价函数为式中:Y'i为模型的实际输出；Yi为模型的期望输出；N为训练样本数目。

步骤3比较粒子的适应值和个体极值BestP处的适应值，取最优者的作为该粒子新的个体极值BestP；比较粒子的适应值和全局极值BestG处的适应值，取最优者作为种群新的全局极值BestG；

步骤 4根据式（10）和式（11），对粒子的位置向量和速度向量进行更新；

步骤 5若达到最大迭代次数kmax或满足网络的精度要求，就停止迭代，输出结果；否则转步骤2。

3 仿真实验分析

3.1 仿真样本的选取

本文收集2013—2014年某型号220 kV、150 MV·A变压器运行数据，从中挑选经吊芯检查后变压器故障类型确定的数据300组，随机选取120组包含各故障类型气体特征量集作训练集，剩余180组作为测试集。

3.2 仿真实验过程

训练抗原集经人工免疫网络处理后即可得到故障诊断模型的隐层中心，仿真中免疫网络相关参数设置为：气体特征量净化阈值cv=0.01，初始抗体个数N=20，最佳抗体选择数n=6，克隆规模Kscale=10，再次选择率 ξ%=10%，克隆选择阈值 δd=0.5，免疫抑制阈值δs=0.15。经人工免疫网络处理后的记忆特征矢量数为11。

以人工免疫网络所得到的结果作为RBF网络模型的初始隐含层中心，用PSO算法对模型权重寻优，相关参数设置为：群体大小m=40；学习因子C1=C2=2；最大惯性因子ωmax=1.4；最小惯性因子ωmin=0.4；最大迭代次数kmax=500，8类故障的期望输出设为10000000 ～00000001。网络的实际输出结果以0～1之间的数值表示对应的故障程度，数值越接近1就表明越有可能发生此类故障，经仿真后得到的适应度曲线如图2所示。从适应度曲线可以看出，在迭代180次左右适应度值趋于稳定，达到了最小约0.02，此时的网络权重即为所求模型的最佳权重。

图2 适应度曲线Fig.2 Fitness curve

3.3 诊断结果

将剩余180组气体特征量用于测试训练后的RBF网络故障诊断模型的诊断精度，仿真实验结果如表2所示。

为了在诊断精度上做对比，本文将收集的故障数据分别采用BP神经网络算法、标准RBF神经网络算法进行故障诊断，结果如表3所示。

由表2可以看出，该模型对不同类型的变压器潜在绝缘故障有不同的诊断准确率，其中y3、y4和y6的诊断准确率达到了100%，分析原因发现这是由于发生这3类绝缘故障时的特征气体差异性较其他故障类明显因而识别率很高，而其余5类故障的平均准确率达到了90%左右。比较表2和表3可以看出本文采用的算法较其他几类算法具有较高故障诊断准确率。

表2 诊断结果Tab.2 Diagnostic result

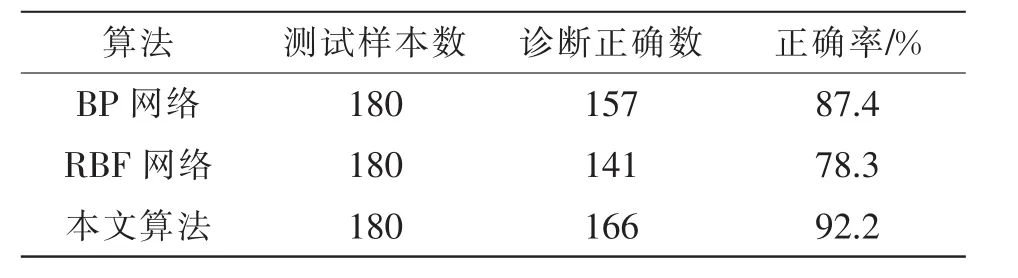
表3 不同诊断算法诊断精度对比Tab.3 Comparison of diagnostic accuracy among different diagnostic algorithms

4 结论

（1）本文以变压器发生内部潜在绝缘故障时的产气成分为依据，实现了对变压器油过热、油纸绝缘中的局部放电等8种具体内部潜在绝缘类型的诊断。与传统只诊断中低温过热、高温过热、低能放电、高能放电等故障类的方法相比有一定的改进。

（2）本文以RBF神经网络算法建立变压器内部潜在绝缘故障诊断模型，针对模型的缺陷与不足引入免疫网络算法与粒子群优化算法对诊断模型优化，提高了模型对变压器内部8种潜在绝缘故障的识别能力，提高了诊断的准确率。实验结果表明，以人工免疫网络算法与粒子群优化算法结合优化诊断模型，可使模型有效地识别变压器潜在绝缘故障类型且识别率可达90%以上。