基于模糊自适应PID控制的机器人运动控制仿真研究
宋昌宝,宋金泽,郑晓圆,李奕陈,李俊龙,冯 雷
(长春工程学院电气与信息工程学院,长春 130012)
0 引言
机器人是一个对周围环境进行感知、行动控制与决策的综合性控制系统,涉及到许多研究方向,其中,对运动控制系统的研究是机器人研究中最基本、最重要的方向。为了实现对机器人更加准确和稳定的控制,目前常见的智能控制方法主要有PID控制、变结构控制、自适应控制、模糊控制以及神经元网络控制等。在实际应用中,使用最为广泛的则是PID控制,它具有结构简单、稳定性好、工作可靠、方便调整等优点,是当下工业控制中的主要控制技术。当被控对象的结构、参数不确定,或得不到精确的数学模型时,又或者其他的控制技术难以应用时,控制系统的结构和参数必须依靠经验和现场调试来确定,这时,PID控制方法是最简单的方法。而自适应控制是在系统的输入或干扰变化较大时,系统能够自动调节地合理参数和控制策略,来达到控制系统对输出量的要求,自适应控制是处理具有“不确定性”的系统的上佳办法,通过观测不确定变量状态来设法降低这种不确定性。控制结果常常能达到所设定的控制指标,因而也被广泛应用于实际中。在模糊控制中,将输入值模糊化,变成模糊变量,确定好模糊变量后还要对其确定隶属函数,以方便确定模糊论域内模糊变量的隶属度值,根据人的直觉思维、实践经验等进行模糊推理从而获得模糊输出,进行反模糊化从而得到清晰的输出量。在生产实践过程中,复杂的控制问题可以通过操作人员的经验和控制理论相结合的方式解决,一般多是应用于实际控制任务复杂而且模型不确定的控制系统中。故本文对模糊自适应PID控制在机器人运动控制中的应用进行了深入研究,从而提高机器人控制的精确度和稳定性。
1 机器人控制系统中电机的数学模型
直流电机的模型如图1所示,直流电动机中,其中电枢回路总电阻R、电感L、电力电子变换器内阻、电枢电阻以及电感和可能在主电路中接入的其他电感、电阻,规定其正方向如图1所示。

图1 直流电动机模型
假设电机在工作时主电路的电流连续,其动态电压平衡方程为:
(1)
式中:E为电动机反电动势(V);Id为整流电流瞬时值(A);L为主电路总电感(H);R为主电路总电阻(Ω),R=Rrec+Ra+RL,其中Rrec为整流装置内阻,包括整流器内部的电阻、整流器件正向压降所对应的电阻、整流变压器漏抗换相压降相应的电阻,Ra为电动机电枢电阻(Ω),RL为平波电抗器电阻(Ω)。
基本运动方程为:
(2)
式中:J为机械转动惯量(kg·m2);ωm为转子的机械角速度(rad/s);θm为转子的机械转角(rad);Te为电磁转矩(N·m);TL为负载转矩(N·m);D为组转矩阻尼系数;K为扭转弹性转矩系数。
忽略阻尼转矩和扭转弹性转矩,可简写为:
(3)
采用工程单位制,式(3)可以写成:
(4)

额定励磁下的感应电动势为:
E=Cen。
(5)
额定励磁下的电磁转矩为:
Te=CmId,
(6)
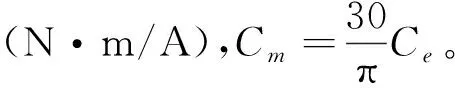
(7)
(8)
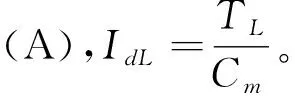
在零初始条件下,对式(7)~(8)进行拉普拉斯变换,得到电压与电流之间的传递函数为:
(9)
电流与电动势间的传递函数为:
(10)
建立精确的模型时,需要考虑电磁时间常数和系统机电时间常数对系统的影响,将其反映在传递函数中,形成一个有反馈的二阶闭环系统,通过对式(9)~(10)的分析,可以得到一个如图2所示的额定励磁下的电机动态结构图。

图2 额定励磁下的电机动态结构图
其开环传递函数为
(11)
2 模糊自适应PID控制
本文结合一般的电机控制,设定以偏差信号e和偏差变化率ec两个变量为输入量,PID控制器的输出作为系统输出量的模糊自适应PID的控制方法,其控制原理如图3所示。
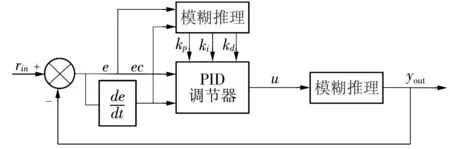
图3 模糊自适应PID控制原理图
为了便于实验与仿真,本文采用ZYN-90-1小型钕铁硼永磁直流电动机进行仿真实验,其参数见表1。

表1 ZYN-90-1小型钕铁硼永磁直流电动机参数
则有:
又:
则:
将Tl、Tm、Ce的值代入电机的仿真模型中,得到如图4所示的仿真模型。

图4 电机仿真模型图
为了验证本文提出的模糊自适应PID算法对机器人运动控制的有限性,我们利用Matlab/Simulink等软件对经典的PID算法和模糊自适应PID算法分别进行仿真研究。为了便于验证,仿真时电机的转速设置为单位阶跃函数,利用PID算法进行电机速度控制时的3个参数的值为:Kp=50,KI=25,KD=0.02,其仿真图形如图5~6所示。未加扰动时的两种算法的仿真结果如图7所示,在15 s时加入0.8 N的扰动时两种算法的仿真结果如图8所示。

图5 经典PID电机控制仿真图

图6 模糊自适应PID电机控制仿真图
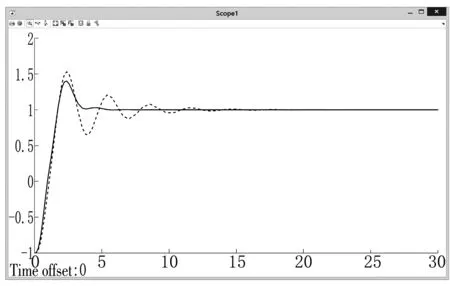
虚线波形:经典PID;实线波形:模糊自适应PID图7 未加扰动时的两种算法的仿真结果

虚线波形:经典PID;实线波形:模糊自适应PID图8 加扰动时的两种算法的仿真结果
4 结论
由仿真图形可以看出,两种PID控制算法全部能够达到对电机精确控制的目的,但本文研究的模糊自适应PID算法较经典PID算法控制有较小的超调量,具有较好的稳定性和可控性,特别是在加入扰动时,本文研究的模糊自适应PID算法具有较短的恢复时间以及较小的超调量。提高了机器人控制的灵敏度,从而满足对机器人较高的控制精度的要求,具有很高的实用性。

