溜井放矿过程中贮矿段井壁动态应力分布特征研究

李 伟 刘艳章，2 邹晓甜 张丙涛

（1.武汉科技大学资源与环境工程学院，湖北武汉，430081；2.冶金矿产资源高效利用与造块湖北省重点实验室，湖北武汉430081）

井壁破坏是矿山溜井常见的故障形式之一［1］。根据井壁破坏部位及其成因，溜井井壁破坏可以分为溜矿段冲击破坏［2］和贮矿段磨损破坏［3］两类。其中，贮矿段井壁的磨损破坏与井壁动态应力息息相关，通常井壁动态应力大的部位受矿石散体的摩擦力也往往较大。随着溜井中矿石散体溜放次数的增加，贮矿段井壁的磨损损伤不断累积，当损伤积累到一定程度时便会导致贮矿段井筒扩径，甚至是井壁垮塌［4-5］。如能获悉矿石运移过程中贮矿段井壁动态应力的分布特征，探寻贮矿段各处井壁磨损破坏程度差异的力学机理，对加强贮矿段井壁维护、优化贮矿段结构、提高溜井生产效率具有重要的理论和实践意义。

溜井中粒径各异的矿石可以认为是一种散体。矿石运移过程中，由于矿石散体颗粒对溜井井壁的冲击磨损作用，导致溜井井壁实际所受的侧压力高于其侧向静压力，这种现象称为超压，由超压现象所引起的实际侧压力称为侧向动压力，即井壁动态应力。目前，关于散体侧压力的研究主要集中在挡土墙、粮仓、料仓等方面，溜井井壁侧压力的研究则相对较少。陈长冰［6］基于大直径筒仓，采用静力平衡法推导了适用于大直径筒仓的浅埋筒壁横向静压力计算公式；Brown［7］采用砂和大豆进行方形筒仓的装卸料模拟实验，测出了筒仓在装料、贮料、卸料3种状态下的应力、应变状态；Khelil和 Belhouchet［8］建立了贮料与圆柱筒仓壁侧压力的平衡方程，获得了仓壁侧压力的分布特征；Martinez和 Alfaro［9］运用有限单元法，对对称卸料过程中筒仓的动压力进行了分析，探讨了震动条件下筒仓的力学性能；原方等［10］等基于散体力学，建立了浅圆仓散料侧压力的计算模型，在假设仓壁极值侧压力呈线性分布的前提下，得到了仓壁总侧压力的计算公式。上述关于散体侧压力的分析方法对溜井贮矿段井壁动态应力的研究具有一定的借鉴意义，但由于散体受限状态不同，物理力学性质亦存在差异，因此上述研究成果并不完全适用于溜井。

本研究以金山店铁矿主溜井为工程背景，推导贮矿段井壁动态应力的理论计算公式并计算不同高度处的井壁动态应力理论值；采用数值模拟及相似试验模拟主溜井放矿过程，对贮矿段井壁不同高度处的动态应力值进行分析；将理论计算、数值模拟、相似试验所得井壁动态应力及相似试验所得井壁磨损分区范围进行对比，验证理论计算公式及研究结果的合理性。

1 金山店铁矿主溜井贮矿段概况

金山店铁矿-410 m至-480 m水平主溜井主要包括溜矿段和贮矿段2部分。其中，贮矿段高38 m，主要由矿仓段和放矿漏斗构成，如图1所示。上部的矿仓为圆形断面，断面直径D=6.0 m，采用C30混凝土支护井壁；下部的放矿漏斗为圆口单侧斜漏斗，放矿漏斗角为55°，上口直径D=6.0 m，下口（放矿口）直径d=3.0 m，采用钢衬板支护漏斗壁。矿石密度约为3 320 kg/m3，含水率控制在3%～5%，储矿高度一般为35.0 m，放矿时通常在井内保留2/3的矿石作为缓冲层，以保护下部放矿设备的安全。主溜井内的矿石块度控制在600 mm以内［11］，粒径分布如表1所示。

2 贮矿段井壁动态应力理论计算

溜井放矿过程中，贮矿段井壁不同高度处所受动态应力的大小不尽相同，如何定量反映矿石流动过程中贮矿段井壁各处动态应力的分布特征，是分析贮矿段井壁磨损破坏程度差异的关键。目前，人们广泛采用Janssen公式［12］计算类筒仓结构单位面积上的垂直静压力，如式（1）所示。

式中，Pv为距容器底板距离为h的测点所在截面上的垂直静压力，Pa；γ为贮料的容重，N/m3；R为筒仓半径，m；f为仓壁与贮料颗粒间的摩擦系数；H为贮料高度，m；h为测点到容器底板之间的垂直距离，m；k为侧压系数。

侧压系数k是依赖于摩擦系数f的无量纲系数，通常由其实用公式算得，如式（2）。当摩擦系数f在0.292～0.625范围内时，λ的取值范围为1.00～1.15［13-14］：

式中，φ为散体颗粒的内摩擦角，（°）。

仓壁的水平压力（侧向静压力）Ph则通过垂直静压力Pv乘以侧压系数k来求解，如式（3）所示。

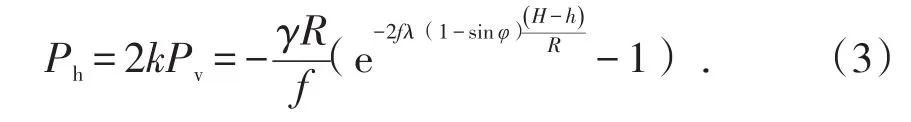
假设溜井放矿漏斗所采取的圆口单侧斜漏斗结构对溜井井壁侧向静压力影响较小，则可利用式（3）计算溜井井壁的侧向静压力。然而，由于矿石对井壁的冲击作用，导致溜井井壁实际所受的侧压力（即侧向动压力）往往高于其侧向静压力。基于此，在溜井井壁侧向静压力计算式（3）中引入超压系数η［15］，推导出因超压现象引起的井壁侧向动压力（即动态应力）Pd的计算公式见式（4）。

式中，超压系数η是指井壁侧向动压力（即动态应力）与静压力之比［16］，通常η＞1且与井壁位置无关。

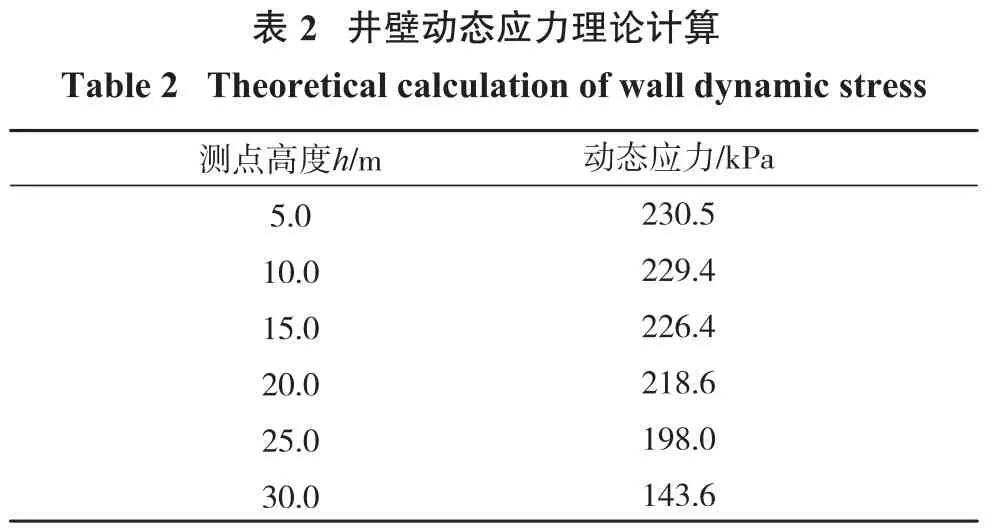
金山店铁矿主溜井内矿石的容重γ为33.20 kN/m3，井筒半径R为3 m，储矿高度H为35 m。关于井壁与矿石散体间的摩擦系数f及内摩擦角φ，文献［11］中作者通过制作半侧井筒配合地质罗盘进行摩擦系数测定试验，最终测得井壁与矿石散体间的摩擦系数f为0.56，采用三轴剪切试验测得矿石颗粒的内摩擦角φ为31.8°［11］。根据摩擦系数f的大小，取λ的值为1.1，将λ和摩擦系数f带入式（2），算得侧压系数k为0.52。超压系数通常在1～1.5之间，本研究取超压系数η为1.3［16］。根据金山店铁矿主溜井贮矿段结构特征，以放矿口所在平面为h值（即测点高度）的零点基准面，在放矿漏斗以上区域，分别对h值为5 m、10 m、15 m、20 m、25 m、30 m高度处的动态应力值进行计算，根据式（4）算得贮矿段井壁不同高度处的动态应力理论值如表2所示。

3 贮矿段井壁动态应力数值模拟

3.1 数值模拟模型构建

根据工程实际建立如图2所示的主溜井贮矿段放矿数值模型，其中，以溜井贮矿段对称面所在平面为典型剖面，放矿漏斗斜壁侧以上的井壁称为贮矿段左壁，放矿漏斗直壁侧以上的井壁称为贮矿段右壁，后文提到的溜井贮矿段左壁与右壁含义均与此处相同。贮矿段井壁及矿石颗粒分别由数值模拟软件中的墙体和单位厚度圆盘生成，矿石含水率由矿石颗粒间的粘结强度及摩擦系数间接表示，主溜井贮矿段结构参数、储矿高度及矿石粒级均与实际参数一致。

3.2 数值模型微观参数赋值

文献［11］中，作者采用文献调研及散体剪切试验等方法，得到了矿石颗粒的微观力学参数，同时测得了矿石颗粒与井壁间的摩擦系数。本研究通过对主溜井内矿石颗粒现场调研资料的分析，结合文献［11］中测定的矿石颗粒微观力学参数及摩擦系数等，确定的数值模型微观力学参数如表3所示。

3.3 数值模拟结果分析

结合理论计算时所取测点高度，分别在图2所示主溜井贮矿段放矿数值模型的左壁与右壁，距离放矿口5 m、10 m、15 m、20 m、25 m、30 m等高度处设置动态应力监测点，对放矿过程中贮矿段井壁动态应力的变化情况进行监测。考虑到放矿过程中矿石颗粒流动的不连续性及矿石颗粒与贮矿段井壁之间接触的不连续性，监测数据以放矿过程中自放矿开始贮矿段井壁所受动态应力的极大值为准。不同高度处溜井贮矿段左壁与右壁动态应力的分布情况如表4所示。

表4中，放矿漏斗之上同一高度处，溜井贮矿段左壁与右壁动态应力值之间尽管存在差异，但相差不大，两者间的最大差值为21.1 kPa，相对于最大动态应力244.6 kPa而言差值不足8.6%；溜井贮矿段左壁与右壁井壁动态应力的均值与其距放矿口的距离呈负相关，放矿口以上（5.0 m，15.0 m）范围内，井壁两侧动态应力的均值均超过了230 kPa；放矿口以上（15.0 m，30.0 m）范围内，井壁两侧动态应力的均值均不足208 kPa。

4 贮矿段井壁动态应力相似试验

4.1 相似试验装置

根据工程实际采用C30混凝土，按相似原理取尺寸相似比为40、井壁材料相似比为1制作溜井贮矿段井筒，矿石材料相似比为1，应力相似比为40，放矿漏斗由钢材料制成［17］。结合数值模型中所取测点位置，在现有溜井放矿相似试验装置［15］基础上，以溜井放矿口为零点基准面，根据相似比，在溜井左壁与右壁，每隔125 mm（对应实际距离5 m）高度对称预留一对应变传感器埋设孔，并埋入LY-350应变式土压力盒，总计埋置12个，配合XL2101G程控电阻应变仪进行不同测点处的井壁应变值监测。应变式土压力盒的埋置方案如图3所示，埋置了应变式土压力盒的溜井放矿相似试验装置如图4所示。

4.2 相似试验矿样制备

试验用矿石取自矿山生产现场，根据金山店铁矿主溜井内实际的矿石粒级分布（见表1）及试验相似比，计算得到试验用矿石粒径如表5所示。将破碎、筛分后的矿样烘干，按3%～5%的含水率计算水的质量并加入烘干矿样中，根据质量配比重新配制矿量。

4.3 相似试验结果分析

试验用矿石配备就绪且设备连接检查无误后，接通应变仪电源并设置好相关参数，将配备好的矿石颗粒注入溜井贮矿段相似试验模型中至875 mm（对应数值模拟35 m）处。考虑到矿石颗粒在自重影响下的压密流动及应变仪的预热过程，矿石注入完毕后需静置1 h。1 h后将系统初始应变值清零，打开溜井放矿口底板放矿的同时点击自动连续采集，采集时间间隔为0.2 s。同组试验重复进行3次，分别取每次试验中各测点处各自应变监测值的极大值，将各测点3次极大值的平均值作为各测点处的应变监测值，根据式（5）带入应变仪的率定参数k和c，将应变监测值转换为对应的动态应力值。

式中，σ为应力值；ε为应变仪的应变监测值；k和c为应变传感器的率定参数。

根据式（5）将溜井贮矿段井壁各位置处的应变监测值换算成相应的应力值后，再通过应力相似比将应力监测值换算成实际值，换算后的井壁动态应力实际值如表6所示。

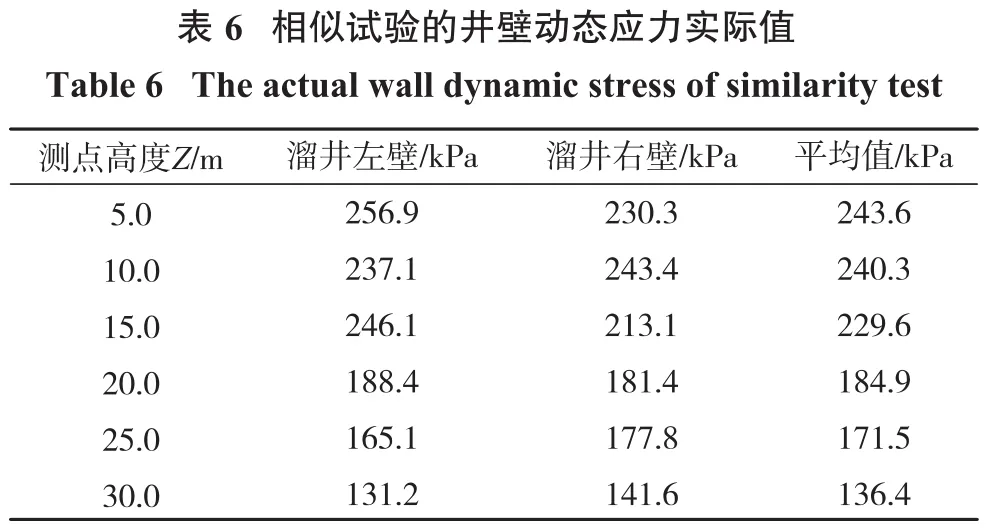
表6中，放矿漏斗之上同一高度处，溜井贮矿段左壁与右壁动态应力值相差不大，两者间的最大差值为33.0 kPa，相对于最大动态应力256.9 kPa而言差值不足12.8%，溜井左右两侧井壁的磨损程度及磨损分区位置基本一致；溜井贮矿段左壁与右壁动态应力的均值与其距放矿口的距离呈负相关，放矿口以上（5.0 m，15.0 m）范围内，井壁两侧动态应力的均值均大于229 kPa，井壁严重磨损［17］；放矿口以上（15.0 m，30.0 m）范围内，井壁两侧动态应力的均值均不足185 kPa，井壁轻微磨损［17］；井壁动态应力越大的部位，井壁磨损程度也越重。

5 贮矿段井壁动态应力对比分析

为了验证贮矿段井壁动态应力理论计算公式及研究结果的可靠性，将理论计算、数值模拟、相似试验所得井壁动态应力分布特征进行对比，对比结果如表7所示。其中，数值模拟和相似试验中放矿漏斗以上同一高度处，由于溜井贮矿段左壁与右壁动态应力相差很小，因此取左壁与右壁动态应力的平均值来表征同一高度处井壁所受动态应力值的大小。此处的相对误差率是指理论计算、数值模拟、相似试验三者所得贮矿段井壁动态应力两两间差值的极大值与相似试验所得贮矿段井壁动态应力值之比。

分析表7可知：理论计算、数值模拟、相似试验所得贮矿段井壁动态应力，在放矿口以上（5.0 m，15.0 m）范围内，均超过了226 kPa，放矿口以上（15.0 m，30.0 m）范围内，均不足208 kPa；三者所得井壁动态应力的最大相对误差率在19%以内，验证了理论计算公式的合理性。

为了更直观地反映贮矿段井壁动态应力分布特征同井壁磨损分区的对应关系，将数值模拟与相似试验所得贮矿段左壁与右壁动态应力分布特征（图5（a））同文献［17］中贮矿段井壁磨损分区范围（图5（b））进行对比，其中，同侧井壁同一高度处的井壁动态应力取数值模拟与相似试验中的极大值，对比结果如图5所示。文献［17］中，利用自主构建的溜井放矿相似试验平台，测定并还原金山店铁矿主溜井贮矿段井壁重磨损区距放矿口的距离为7.0～14.28 m，距放矿口14.28 m以上区域为轻磨损区。

分析图5可知，井壁动态应力分布云图（a）中，放矿漏斗放矿口以上（5.0 m，15.0 m）范围内，井壁动态应力较大，放矿口以上（15.0 m，30.0 m）范围内，井壁动态应力较小；数值模拟和相似试验中，尽管放矿漏斗以上溜井贮矿段左壁与右壁动态应力之间存在差异，但两者间的差值很小，两者间的最大差值相对于最大动态应力而言差值不足12.8%（相似试验），对整个溜井贮矿段井壁动态应力分布特征的研究影响较小，理论计算时将圆口单侧斜漏斗结构对放矿漏斗以上井壁动态应力分布的影响忽略是可行的。井壁磨损分区范围图（b）中，放矿口以上7.0～14.28 m范围内为重磨损区，距放矿口14.28 m以上为轻磨损区。本研究所得溜井贮矿段井壁动态应力分布特征，同文献［17］中采用相似试验所得溜井贮矿段井壁磨损分区结果能够相互对应，井壁动态应力越大则井壁磨损程度也越重。

6 结论

本研究针对溜井放矿过程中贮矿段井壁频繁发生的磨损破坏问题，以金山店铁矿主溜井为工程背景，推导了贮矿段井壁动态应力的理论计算公式，并通过数值模拟、相似试验对理论计算结果进行了验证。综合对比理论计算、数值模拟、相似试验所得井壁动态应力分布特征同井壁磨损分区的对应关系，验证了研究结果的合理性，从力学角度解释了贮矿段各处井壁磨损程度差异的原因。

（1）三者所得贮矿段井壁动态应力最大相对误差率在19%以内，井壁动态应力分布特征同井壁磨损分区结果能够相互印证，验证了理论计算公式的合理性。

（2）三者所得贮矿段井壁动态应力与其距放矿口的距离呈负相关；三者所得井壁动态应力的均值，在放矿口以上（5.0 m，15.0 m］范围内均超过了228 kPa，在（15.0 m，30.0 m］范围内均不足204 kPa，分别对应于相似试验中井壁的重磨损及轻磨损区；井壁动态应力越大的部位，井壁磨损程度也越重。