流固耦合作用对筒装料管道车水力输送内部流场特性的影响

张春晋，孙西欢,2※，李永业，张学琴，张雪兰，杨小妮,4，李 飞



流固耦合作用对筒装料管道车水力输送内部流场特性的影响

张春晋1，孙西欢1,2※，李永业1，张学琴3，张雪兰1，杨小妮1,4，李 飞1

（1. 太原理工大学水利科学与工程学院，太原 030024；2. 晋中学院，晋中 030600； 3. 章丘黄河河务局，济南 250200；4. 太原理工大学现代科技学院，孝义 032300）

为了进一步分析流固耦合作用对筒装料管道水力输送内部流场特性的影响，采用商用ANSYS Fluent 12.0软件对管道流体域与管道车固体域进行联合求解，并将耦合计算的模拟值与试验值进行对比。管道流体域非稳态计算采用雷诺时均动量方程和RNG-湍流模型，管道车固体域瞬时速度与位移的耦合计算采用结构动力学方程。结果表明：模拟值与试验值基本吻合，且管道车运移时瞬时速度、脉动压强、流速分布以及压强分布的最大相对误差分别不超过1.43 %、3.16 %、5.28 %和1.64 %，得到采用流固耦合方法求解筒装料管道水力输送的内部流场特性是可行的；随着径长比的增加，管道车车前近壁面区域的轴向流速、径向流速与压强的影响范围增大，涡量幅值的影响范围减小，周向流速的影响范围呈先减小后增大；管道车下游流场的能量耗散与能量转化共同引起了管道车车前近壁面区域出现了低压区，而能量转化使得管道车下游流场的压强又再次回升；管道车的时均压降系数随着径长比的增加呈先减小后增大，且径长比为0.7的管道车时均压降系数最小。该文的研究将为管道车的结构设计与动力学机理分析提供理论参考。

流场；压强；农产品；流固耦合；流场特性；管道车；径长比；耦合模型

0 引 言

近年来，农产品物流依赖于公路、铁路等传统运输方式[1]。传统运输方式在提高农产品运输效率的同时还造成了能源危机和环境污染[2]。筒装料管道水力输送便是在此基础上提出的一种低碳环保的农产品运输方式，该运输方式是将农产品装盛并密封在圆柱状的管道车内部，依靠水流的作用推动管道车在有压管道内部进行长距离的运输[2]，其具有输送成本低与环境污染小的特点。

近年来，许多国内外专家对筒装料管道水力输送展开了大量研究。试验方面：王锐等[3]、Ulusarslan等[4]通过分析动力学特性划分了管道车运移阶段。齐佳佳[5]、Sub等[6]及Huang等[7]探究了不同因素对管道车时均速度的影响。郭晓朦[8]、王琪[9]和Wang等[10]采用高速摄像机测量了管道车瞬时加速度。李永业等[11]和Lenau等[12]分析了不同型号管道车在管道内运移时的流场特性。以上研究成果受到测量仪器的限制，管道流场特性未能全面获得。模拟方面：Barthès-Biesel[13]和Vlasak等[14]结合湍流关系分析了管道车瞬时能耗。Kroonenberg[15]、Cheng等[16]和Zhang等[17]采用湍流模型分析了环状缝隙区域的流速与压强。李永业等[18]、Khalil等[19]和Asim等[20]采用计算流体力学软件求解了管道车运移的流场分布。模拟研究将管道车视为匀速运移，仅考虑了管道车对流场的影响。事实上管道车在流体的作用下也产生动力学响应。如果不考虑两者的耦合作用，这将造成模拟结果与实际不符。

目前，流固耦合研究主要应用于离心泵、风机等]领域[21，对于筒装料管道水力输送还鲜有涉及。本文采用ANSYS Fluent 12.0软件对管道流体域和管道车固体域进行联合求解，揭示管道车运移时管道内部的流场特性。

1 材料与方法

1.1 试验系统

管道车由料筒、支撑体及万向滚珠组成[3]，如图1所示。料筒端面布置互成120°的支撑体，支撑体使管道车与管道保持同心[8]。万向滚珠安装在支撑体尾端，减小管道车与管道的摩擦阻力。试验系统包括动力装置、调节装置、输送装置及回收装置[2]，如图2所示。动力装置包括试验水箱和离心泵。调节装置包括电磁流量计、调节阀和制动装置。回收装置由投放口、塑料集车箱及稳流板组成。

采用DANTECH公司的多普勒激光流速仪和江苏扬泰光电公司的光电计时器测量管道流速。苏州轩胜仪表科技有限公司的压力传感器测量管道的测压管压强。成都泰斯特电子公司的标准动态压强采集系统收集压力传感器测量的时均压强和脉动压强的信号，并传输至计算机。Memrecam GX-3高速摄像机记录管道车瞬时位移与速度。

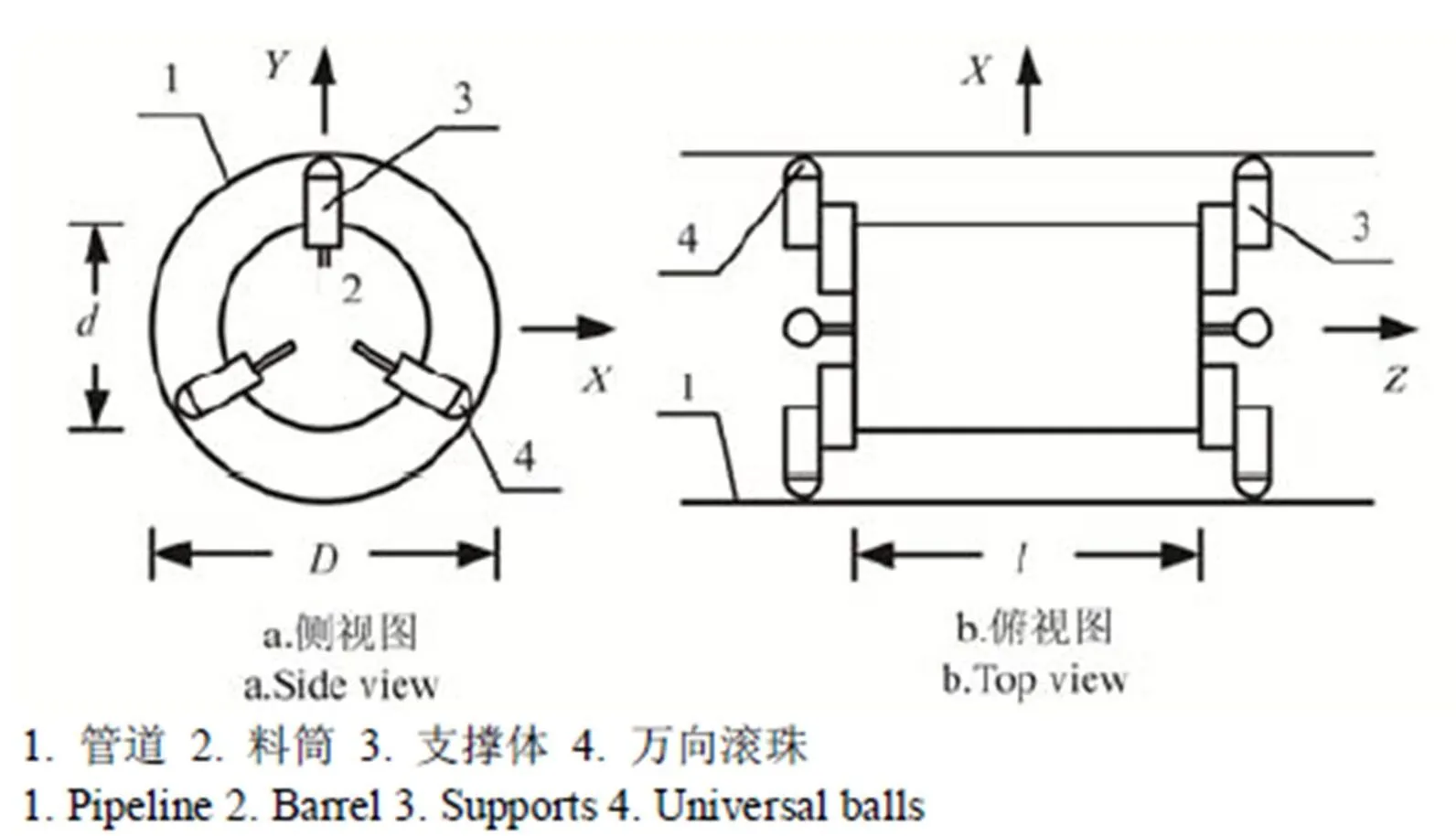
注：X, Y和Z分别表示笛卡尔坐标系中3个不同的方向；D表示管道直径，m；d表示料筒直径，m；l表示料筒长度，m。

1.2 试验设计

影响筒装料管道水力输送特性的因素包括管道直径、料筒长度、荷载、管道流量及管道车的径长比等。管道车的径长比k指料筒直径与其长度的比值。该文探讨了不同径长比条件下筒装料管道水力输送的内部流场特性，为此以径长比作为控制因子。试验方案中管道直径设置为0.1 m。料筒长度取决于输送装置中弯管段的曲率半径，且料筒长度越大管道车盛装物料的空间就越大。根据弯管段曲率半径，料筒长度设置为0.1 m。管道车的径长比为0.5、0.6、0.7和0.8共4个水平值，选择依据：当径长比小于0.5时，管道车输送物料的能力较低；当径长比大于0.8时，管道车将无法在弯管段灵活运移。根据4种径长比管道车料筒的内部体积，荷载设置为0.6 kg。根据管道车临界起动的管道流量，管道流量设置为50 m3/h。

试验测试段全长为5.8 m，距下游弯管段进口断面2.7 m，距上游制动装置4.7 m，如图2所示。

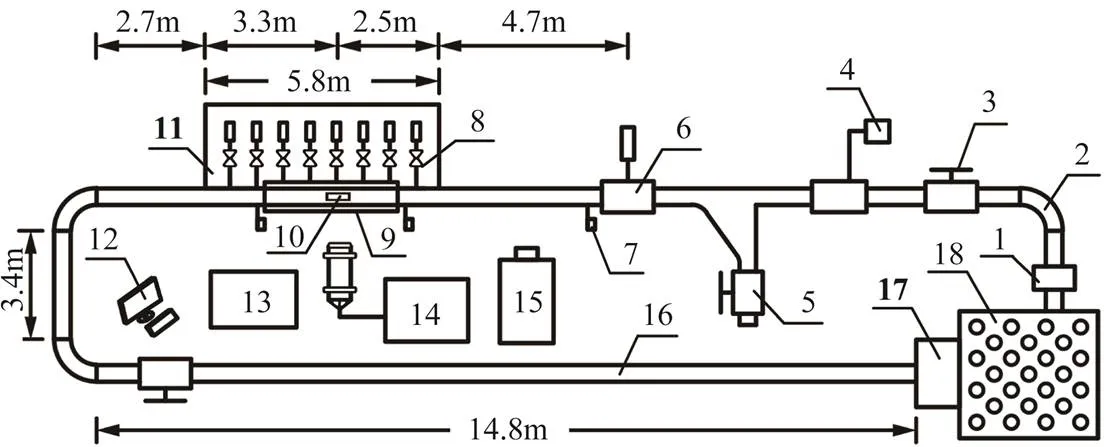
1.离心泵2.钢管段3.调节阀4.电磁流量计5.管道车投放口6.制动装置7.光电计时器8.压力传感器9.水套10.管道车11.试验测试段12.计算机13.标准动态压强采集系统14.多普勒激光流速仪15.高速摄像机16.平直管段17.塑料集车箱18.试验水箱和稳流板。

管道下游距试验测试段进口断面2.6 m的位置设置1个流速测试断面，即1#断面，如图3所示。流速测点位于7个等间距水平线与五等分测环的交点，共布置43个流速测点。试验测量中，测量流速是在管道车中心运移至距试验测试段进口断面2.5 m位置时得到的，此时管道车位于1#断面上游0.1 m的位置。压强测点沿试验测试段均匀布置在管道壁面，间隔为0.5 m，共布置12个压强测点，如图3所示。试验时，每个试验测点重复测量3次，并取其平均值。

注：1′~12′ 表示12个压强测点位置。

2 数值计算

2.1 几何模型

应用Pro/E 5.0软件建立筒装料管道水力输送的几何模型。几何模型包括平直管段和管道车。平直管段5.8 m，直径0.1 m。平直管段划分为进口管段、运移管段及出口管段[20]。进口管段0.5 m，考虑到管道内部湍流的充分发展。出口管段0.5 m，以降低管道车对出口压强的影响。数值计算中料筒结构与试验方案中料筒结构完全一致。管道车的料筒长度设置为0.1 m，且料筒直径分别设置为0.05、0.06、0.07和0.08 m。支撑体由细圆柱体和薄金属板组成。细圆柱体高0.02 m，直径0.008 m。万向滚珠为半球状，直径为0.008 m。初始状态时管道车中心距进口断面0.7 m。管道流量分别设置为40、50和60 m3/h。

2.2 流体域控制方程

采用ICEM软件对几何模型网格加密。计算域分为管道流体域与管道车固体域。运移管段采用四面体非结构化体网格加密，进口与出口管段采用与四面体网格相同尺寸的六面体结构化体网格加密。网格疏密对数值模拟的影响较大，以几何模型进口断面的时均压强作为参考，对管道流体域网格无关性[22]进行考察，如表1所示。

定义采用相邻两种体网格尺寸划分几何模型时进口断面时均压强的相对误差为

式中1和2分别为相邻较大和较小体网格尺寸条件下进口断面的时均压强值，Pa。

数值模拟中为了提高计算结果的精度，采用的体网格尺寸需要远小于计算域的结构尺寸，因此认为网格无关性检验的最大网格尺寸设置为0.002 8 m是合理的。

根据表1检验结果，得出由0.002 m体网格和0.0022 m体网格所得到的几何模型的进口断面时均压强的相对误差不超过0.47%。定义当<0.5 %时，体网格尺寸对于几何模型的进口断面时均压强的影响可以忽略不计，认为满足网格无关性要求。同时将模拟值与试验值对比，得到模拟值与试验值基本一致，且最大相对误差不超过1.26 %。综合分析得出当体网格尺寸小于0.002 m时已达到了计算结果与网格划分无关的要求，因此采用0.002 m的体网格类型划分几何模型计算域中的管道流体域。管道车移动壁面和管道固定壁面边界近壁面流速梯度较大，需采用边界层加密。根据y合理范围计算得到第1层网格厚度是2.53×10-4m (y=30)，层间比例为1.1。

表1 网格无关性检验（Q=50 m3/h）

注：k表示管道车的径长比，表示管道流量，m3·h-1，表示进口断面的时均压强，Pa。

Note:krepresents diameter-length ratio of piped carriage,represents pipe discharge, m3·h-1,represents time-average pressure of inlet cross-section, Pa.

笛卡尔坐标系中，连续性方程和雷诺时均动量方程可表示为[23]

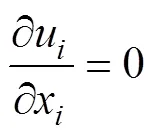
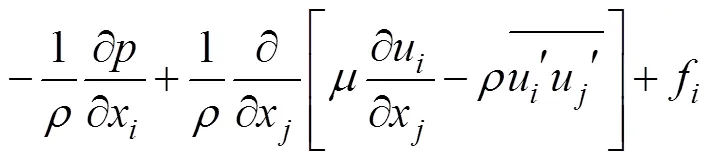
RNG-湍流模型能够处理复杂的湍流问题[24]。因此采用RNG-湍流模型进行计算。该文采用PISO算法，其中动量方程、湍动能方程及湍流耗散率方程的对流项均采用二阶迎风格式，而扩散项采用中心差分格式[25]。

进口边界为流速进口，通过经验公式[26]计算进口边界和值；出口边界为压力出口；管道壁面采用无滑移边界[27]；管道车动边界采用6DoF（6 Degree of Freedom）耦合模型。该模型涉及管道车转动惯量与摩擦阻力。

转动惯量[28]是管道车的旋转阻力矩，表示为

摩擦阻力是管道车的运移阻力，表示为

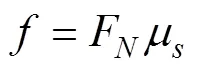
式中J、J和J分别为管道车3个方向的转动惯量，kg·m2；为料筒直径，m；为料筒长度，m；为管道车总质量，kg；F为支撑力，N；μ为滚动摩擦阻力系数，经试验测量，滚动摩擦阻力系数为0.428。管道车初始速度为管道车经过试验测试段进口断面的实测瞬时速度。

2.3 结构动力学方程

6DoF耦合模型中，结构动力学方程求解管道车在任意时刻速度与位移。该方程[29]表示如下

式中为水平合力，N；a为加速度，m/s2；为外力矩，N·m；为转动惯量矩阵；ω为角速度，rad/s。

2.4 流固耦合求解算法

6DoF耦合模型分析流程[30]如下：1）首先需要设定在初始时刻，管道车速度、角速度、角度及位移；2）将管道车在时刻的运移速度、角速度作为下一时刻边界条件，求解在+D时刻流场的水力特性，并获得合力F和外力矩M；3）计算在+D时刻的速度、位移、角速度和角度；4）结合位移t c和转动角度t+t c，利用动网格技术将管道车移动到新位置，并更新管道流体域网格；6）将管道车在D时刻的速度、角速度作为下一时刻的边界条件，并不断重复上述过程。

3 结果与分析

3.1 管道车瞬时速度模拟与验证

图4为管道流量为50 m3/h时，管道车瞬时速度模拟值与试验值对照图。该文中用于试验验证的管道流量仅为50 m3/h，因此在第3章节中主要分析了管道流量为50 m3/h时的筒装料管道水力输送的内部流场特性。

由图4中可知：1）模拟值与试验值一致，且最大相对误差不超过1.43 %；2）随着径长比的增加，管道车时均速度呈增长趋势。原因是径长比的增加，引起管道车的浮力增加，导致时均速度增大；3）管道车瞬时速度在一定范围波动，可将管道车运移视为恒定运移；4）管道车运移时瞬时速度呈无规则波动。原因是流体脉动压强的无规则波动引起流体对管道车的瞬时荷载产生波动。

3.2 脉动压强波形模拟与验证

图5为管道流量为50 m3/h时，不同测压管脉动压强振幅频谱模拟值与试验值对照图。图5中3′和5′测压管分别距试验测试段的进口断面为1.0和2.0 m。

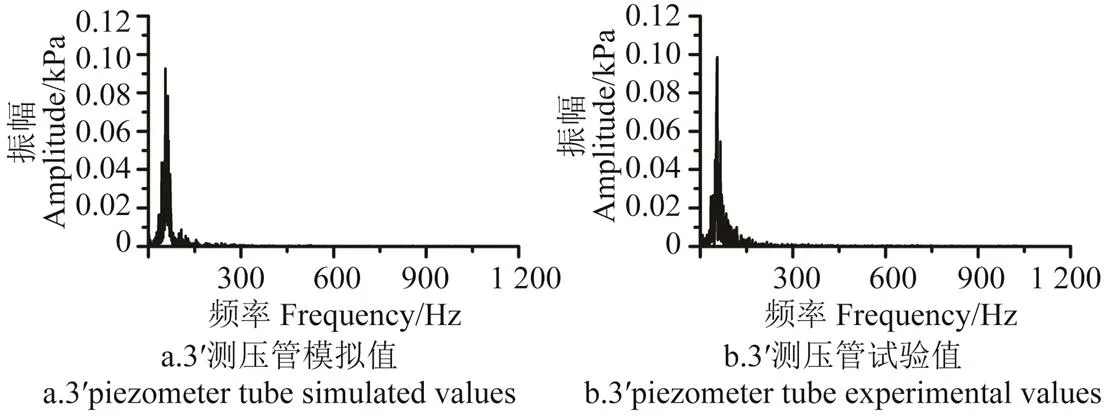
由图5中可知：1）模拟值与试验值一致，且最大相对误差不超过3.16%；2）测压管脉动压强集中在20~100 Hz频带，脉动主频率55 Hz，相应振幅0.1 kPa。脉动压强是以时间为参数的随机过程，由管道内湍流流动引起。

3.3 模型流速分布模拟与验证

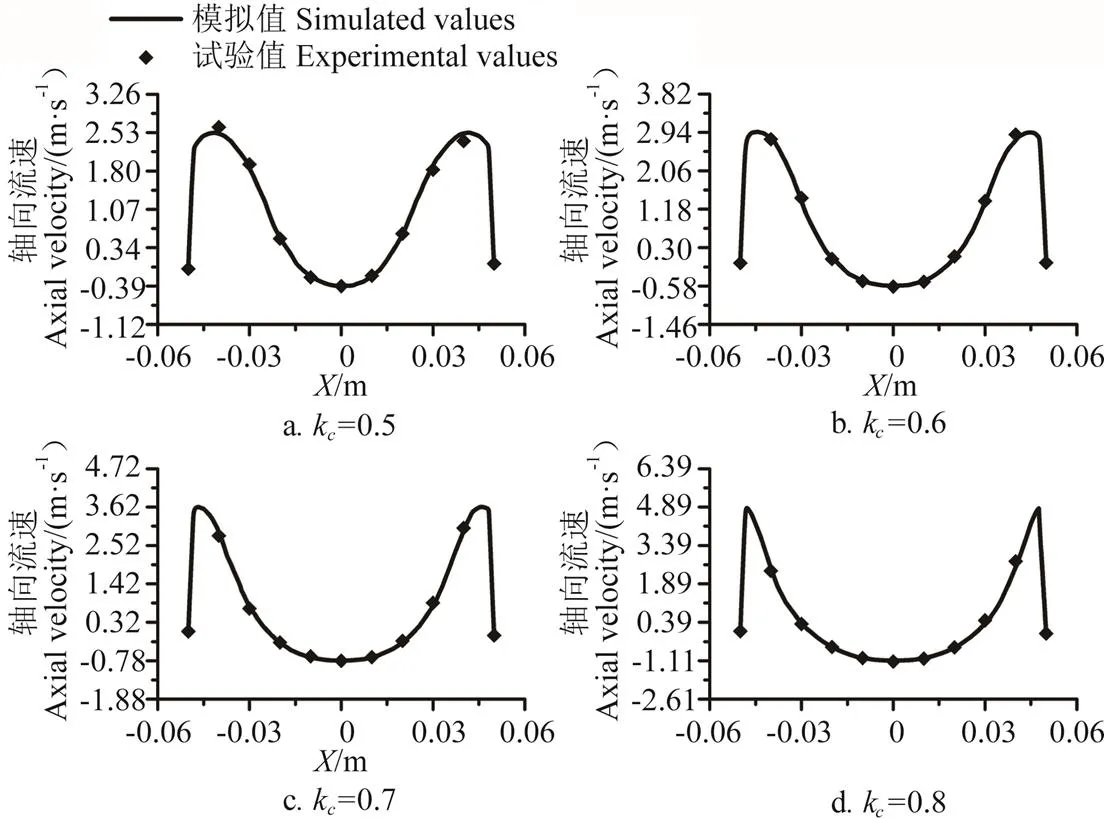
图6为管道流量为50 m3/h时，当管道车中心运移至距离试验测试段的进口断面2.5 m位置时，管道流场1#断面水平极轴处的轴向流速模拟值与试验值对照图。

由图6中可知：1）模拟值与试验值一致，且最大相对误差不超过5.28 %；2）管道车车前近壁面流场区域存在明显回流。原因是环状缝隙流体过渡到管道车下游流场时引起了边界层分离，导致管道车下游流体回填管道车车前的空腔区域；3）随着径长比的增加，管道车下游流场的回流范围增大。原因是回流区域仅存在于管道车车前的近壁面区域，径长比的增加，引起回流范围增加。

图7为管道流量为50 m3/h时，管道车运移时水平断面的轴向流速分布云图。

注：X表示面向平直管道下游时水平向左的方向。

注：Sc表示管道车中心到几何模型进口断面的距离，Vc表示管道车的瞬时速度，矩形的空白区域表示管道车，X表示面向平直管道下游时水平向左的方向，Z表示平直管道流体流动的方向。

由图7中可知：1）管道车车前近壁面区域形成了“锥形”的回流范围。原因是管道车壁面边界层存在逆压梯度，引起环状缝隙流出现了边界层分离；2）随着径长比的增加，管道车下游流场回流范围增大。原因是回流范围存在于管道车车前近壁面区域，径长比的增加引起车前近壁面区域增大；3）环状缝隙进口和管道车下游的管道近壁面出现2处高流速区。环状缝隙进口高流速区是由于边界层分离引起主流断面减小，使得轴向流速增加。而管道车下游的管道近壁面高流速区是由于回流流体与管道车车前端面相互作用，导致回流流体向管道近壁面高速扩散；4）随着径长比的增加，管道车对上游流场的影响范围减小。原因是径长比越大，管道车运移速度越接近流体平均轴向流速，使得管道车对流场扰动减小；5）不同时刻管道车近壁面区域轴向流速分布一致。原因是管道车瞬时速度变化幅度较小，导致管道车在任意时刻与管道流体形成的耦合系统的轴向流速分布一致。

图8为管道流量为50 m3/h时，管道车运移时水平断面的径向流速分布云图。

图8 管道车运移时水平断面的径向流速分布

由图8中可知：1）径向流速分布于管道车车前、后的近壁面区域，且径向流速由管中心指向壁面。原因是流体受到管道车车后端面的影响，使得流体向环状缝隙流动时流线产生收缩。而管道车的车前近壁面区域的径向流速由回流流体所引起，回流流体受到管道车车前端面的阻碍向管道壁面扩散；2）随着径长比的增加，管道车车前近壁面区域的径向流速影响范围增大。原因是径长比越大，引起管道车车前端面与其下游回流流体相对速度增大，导致径向流速的影响范围增大；3）不同时刻管道车运移时的径向流速分布一致。原因是管道车瞬时速度变化幅度较小，导致管道车在任意时刻与管道流体所形成的耦合系统的径向流速分布一致。

图9为管道流量为50 m3/h时，管道车运移时水平断面的周向流速分布。

由图9中可知：1）支撑体的近壁面区域周向流速最大。原因是管道车车前、后近壁面区域流场的周向流速由支撑体所引起；2）管道车车后端面的周向流速较小。原因是车后端面与管道车上游流体的相对速度较小；3）虽然环状缝隙流与管道车下游回流流动方向相反，但在同一侧形成的周向流速方向一致；4）随着径长比的增加，管道车车前近壁面区域的周向流速影响范围呈先减小后增大。原因是当径长比小于0.7，车前近壁面区域的周向流速由环状缝隙流绕流支撑体形成。当径长比大于0.7，车前近壁面区域的周向流速由回流流体绕流支撑体形成；5）不同时刻管道车运移时周向流速分布一致。原因是管道车瞬时速度变化幅度较小，导致管道车在任意时刻与管道流体所形成的耦合系统的周向流速分布一致。

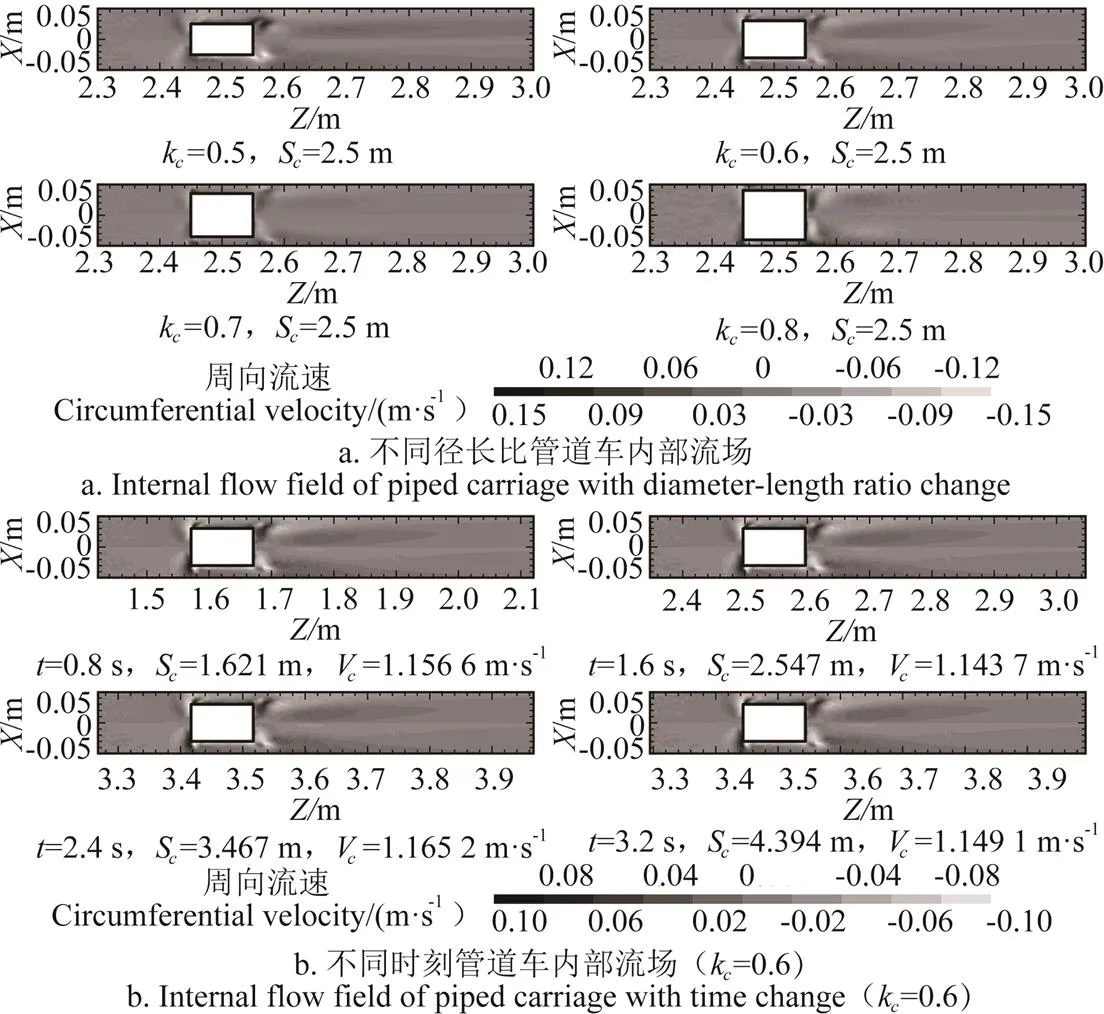
图9 管道车运移时水平断面的周向流速分布

3.4 模型压强分布模拟与验证

图10为管道流量为50 m3/h时，当管道车中心运移至1#断面上游0.1 m时，试验测试段区间管道沿程测压管的时均压强模拟值与试验值对照图。

由图10中可知：1）模拟值与试验值基本一致，且最大相对误差不超过1.64 %；2）管道车近壁面流场呈“W”型的时均压强分布。原因是管道流体受到管道车车后端面支撑体的作用，引起断面收缩，导致管道的时均压强降低。随后流体进入环状缝隙，流速降低使得在环状缝隙的时均压强回升。在管道车下游区域，流体从环状缝隙逐步过渡到管道车下游流场产生边界层分离，引起旋涡损失，使得时均压强急剧降低。但是流体在发生能量耗散的同时还发生能量转化，环状缝隙流扩散时将动能转化为下游流体的压能，使得流体压强再次回升；3）随着径长比的增加，管道车的车前近壁面区域的时均压强的压降增加。原因是径长比的增加，引起了管道车车前流场回流增加，导致边界层分离引起的能量耗散增加。

图11为管道流量为50 m3/h时，管道车运移时水平断面的压强分布云图。

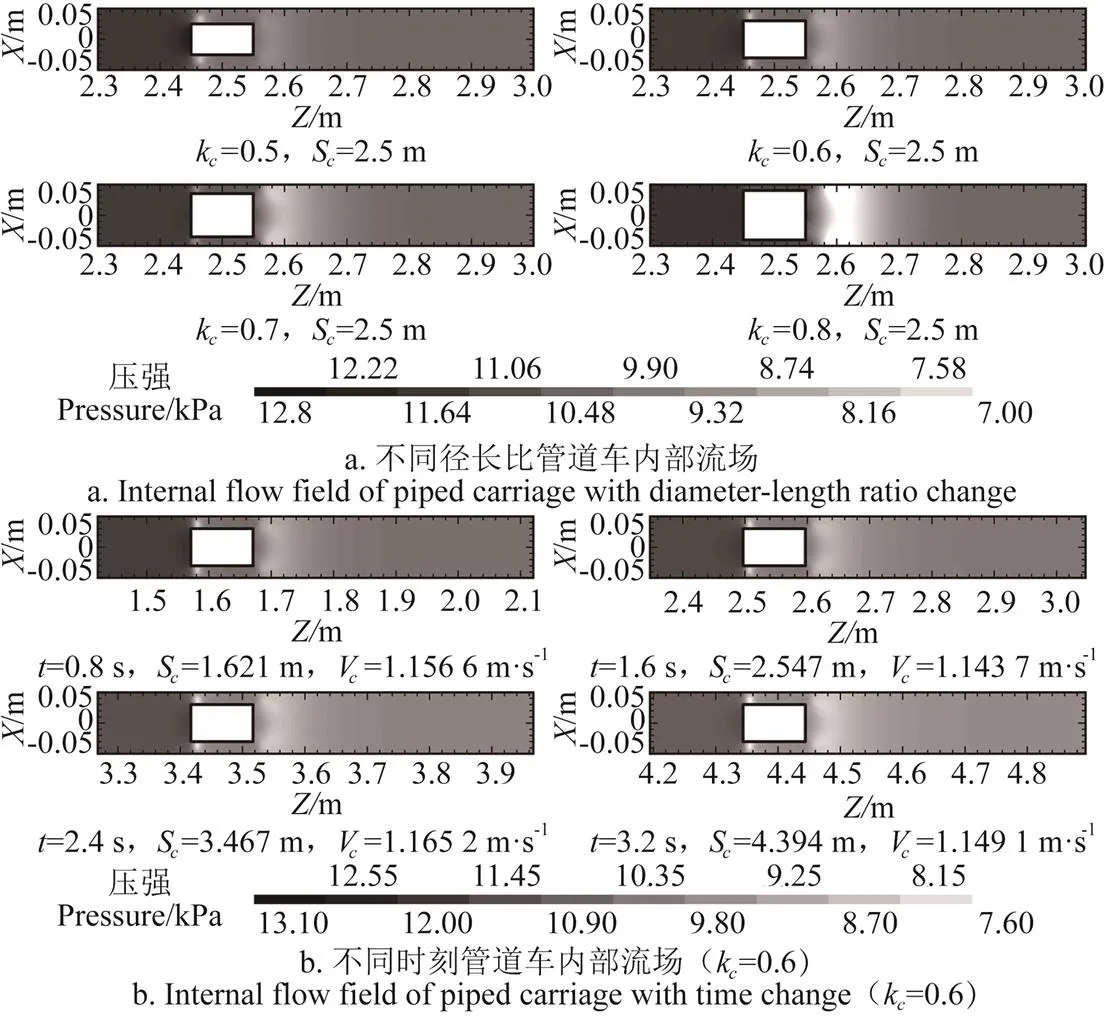
图11 管道车运移时水平断面的压强分布

由图11中可知：1）管道流场高压区存在于管道车车前、后近壁面区域。原因是车后近壁面区域流体在管道车的作用下流体动能转化为压能，管道车的车前近壁面区域的回流流体与车前端面发生碰撞，引起流体动能转化为压能；2）管道车环状缝隙进口和管道车车前近壁面存在低压区。原因是在管道环状进口区域和管道车的车前近壁面区域发生了边界层分离；3）管道车下游流场存在低压区，而低压区下游流场压强又再次升高。原因是环状缝隙流与管道车下游流体发生相互掺混，引起能量耗散与能量转化。能量耗散和能量转化引起管道车下游流场出现低压区，能量转化使得低压区域下游的压强再次回升；4）随着径长比的增加，管道车的车后近壁面区域的高压区范围减小。原因是径长比的增加，使得管道车的车后端面与其上游流体的相对速度减小，引起流体动能转化为压能的程度降低；5）随着径长比的增加，管道车下游流场压降幅度增大。原因是径长比的增加，引起管道车下游流场旋涡能量耗散程度增强；6）随着管道车运移时间的增长，管道车局部压强呈现出整体降低的趋势。原因是管道车局部压强与管道沿程压强变化一致。由于管道内部压强沿程降低，所以当管道车越靠近管道下游流场，管道车近壁面区域压强也呈现降低趋势。

3.5 涡量分布模拟

图12为管道流量为50 m3/h时，管道车运移时水平断面的涡量幅值分布云图。

由图12中可知：1）涡量幅值分布在环状缝隙进口的管道车近壁面和环状缝隙流与其下游流体混流的交界面。原因是环状缝隙进口的管道车近壁面区域存在边界层分离，形成局部涡量。而环状缝隙流与其下游流体的交界面处存在2股流体掺混，形成局部涡量；2）随着径长比的增加，管道车车前近壁面区域的涡量幅值影响范围减小。原因是径长比越大，在管道车车前近壁面区域的回流范围就越大，使得旋涡在极短范围内衰减；3）随着径长比的增加，环状缝隙进口处管道车近壁面区域的涡量幅值和管道车下游流场的涡量幅值均增大。原因是径长比的增加，使得边界层分离现象越明显，导致流场涡量幅值增大；4）管道车运移对管道流体产生局部扰动，因此流场涡量幅值分布于管道车近壁面区域。由于管道车瞬时速度的变化幅度较小，导致管道车在任意时刻与管道流体形成的耦合系统的涡量幅值未出现时空演变。

图12 管道车运移时水平断面的涡量幅值分布

图13为管道流量为50 m3/h时，管道车运移时不同时刻水平断面的3维涡量分布云图。

由图13中可知：1）管道车运移时水平断面的周向涡量变化范围明显大于轴向涡量和径向涡量的变化范围。原因是周向涡量是由于流体绕流管道车料筒时产生的，而轴向涡量和径向涡量是由于流体绕流支撑体时形成的。由于管道车的料筒对管道流体的扰动较大，因此管道车运移时水平断面的周向涡量变化幅度较大；2）管道内部轴向涡量和周向涡量分别沿轴正负方向呈大小相等、方向相反的涡量分布。原因是管道车在水平断面的投影呈对称结构，因此轴向涡量和周向涡量分别沿轴正负方向呈对称分布；3）管道内部径向涡量分别沿轴正负方向呈现相同的涡量分布。原因是轴正负方向处的径向涡量均为绕流对称分布的支撑体形成的，因此管道水平断面的管中心两侧径向涡量分布相同；4）管道车运移时不同时刻管道水平断面的3维涡量分布一致，未出现明显的时空演变。原因是管道车稳定运移时其瞬时速度变化幅度较小，使得管道车与管道流体之间组成的耦合系统的瞬态运动要素处于恒定状态，因此管道车运移时不同时刻的3维涡量分布基本相同。

图13 管道车运移时不同时刻水平断面3维涡量分布

3.6 时均压降系数模拟

图14为不同管道流量条件下，管道车时均压降系数与径长比之间的变化曲线。能耗损失采用压降系数表征[20]，压降系数指总能耗与空管道流体能耗的比值。该文采用时均压降系数分析管道车在平直管段运移的能耗。

图14 管道车时均压降系数与径长比之间的变化曲线

由图14中可知：1）随着径长比的增加，管道车时均压降系数呈先减小后增大，且径长比为0.7的管道车时均压降系数最小。原因是当径长比小于0.7，管道车的运移速度起主导作用，运移速度越快能耗越小。而当径长比大于0.7，管道车直径起主导作用，直径越大能耗就越大；2）管道流量越大，时均压降系数就越小。原因是管道流量越大使得空管道流体的沿程能耗损失逐渐增加。

4 结 论

1）随着径长比的增加，管道车的车前近壁面区域的轴向流速、径向流速及压强影响范围增大，涡量幅值影响范围减小，周向流速影响范围呈先减小后增大。

2）管道车下游流场的能量耗散与能量转化共同引起了管道车的车前近壁面区域出现低压区，而能量转化又使得管道车的下游流场的压强再次回升。

3）随着径长比的增加，管道车时均压降系数呈先减小后增大，且径长比为0.7的管道车时均压降系数最小。

4）管道车沿管道向下游运移时，管道车近壁面流场区域的轴向流速、径向流速、周向流速及涡量幅值分布基本一致，而压强分布却呈逐渐降低的变化趋势。

[1] 孙曦，杨为民. 低碳经济环境下农产品运输与配送问题研究[J]. 江苏农业科学，2014，42(4)：392－395. Sun Xi, Yang Weimin. Research on problems of transportation and distribution of agricultural products under the environment of low carbon economy[J]. Jiangsu Agricultural Sciences, 2014, 42(4): 392－395. (in Chinese with English abstract)

[2] 孙西欢，李永业，阎庆绂. 筒装料管道水力输送管道车起动条件的试验研究[C]// 朱德祥. 第二十届全国水动力学研讨会文集. 北京：海洋出版社，2007：425－431. Sun Xihuan, Li Yongye, Yan Qingfu. Experimental study on starting conditions of the hydraulic transportation on the piped carriage[C]//Zhu Dexiang. Proceedings of the 20th national conference on hydrodynamics. Beijing: China Ocean Press, 2007: 425－431. (in Chinese with English abstract)

[3] 王锐，孙西欢，李永业. 管道车在不同雷诺数条件下的输送特性[J]. 排灌机械工程学报，2011，29(4)：343－346，358. Wang Rui, Sun Xihuan, Li Yongye. Transportation characteristics of piped carriage with different Reynolds numbers[J]. Journal of Drainage and Irrigation Machinery Engineering, 2011, 29(4): 343－346, 358. (in Chinese with English abstract)

[4] Ulusarslan D, Teke I. An experimental investigation of the capsule velocity, concentration rate and the spacing between the capsules for spherical capsule train flow in a horizontal circular pipe[J]. Powder Technology, 2005, 159(1): 27－34.

[5] 齐佳佳. 不同径长比管道车在平直管段运移时的环隙流速特性研究[D]. 太原：太原理工大学，2016. Qi Jiajia. The Research on Slit Flow Velocity of Stable Moving Piped Carriage with Different Slenderness Ratios[D]. Taiyuan: Taiyuan University of Technology, 2016. (in Chinese with English abstract)

[6] Sub I, Chaddock J B. Drag calculations for vehicles in very long tubes from turbulent flow theory[J]. Journal of Fluids Engineering, 1981, 103(2): 361－366.

[7] Huang S B, Li Z M. Heat transfer of Bingham fluid in a concentric annulus with an axially moving inner pipe[J]. Journal of China University of Petroleum, 2007, 31(3): 94－99.

[8] 郭晓朦. 不同输送荷载管道车在平直管道运行时的车后水力特性研究[D]. 太原：太原理工大学，2015. Guo Xiaomeng. Turbulence Characteristics of Hydraulic Pipeline Transportation under Different Load in Straight and Horizonal Pipeline[D]. Taiyuan: Taiyuan University of Technology, 2015. (in Chinese with English abstract)

[9] 王琪. 基于高速摄像技术的管道车运动特性试验研究[D]. 太原：太原理工大学，2016. Wang Qi. Experimental Study on Motion Characterisics of the Capsule Based on High Speed Imaging Technology[D]. Taiyuan: Taiyuan University of Technology, 2016. (in Chinese with English abstract)

[10] Wang Z, Sui Y, Salsac A –V, et al. Motion of a spherical capsule in branched tube flow with finite inertia[J]. Journal of Fluid Mechanics, 2016, 806(11): 603-626.

[11] 李永业，孙西欢，李飞，等. 不同型号的管道车在管道中运移的水力特性[J]. 排灌机械工程学报，2010，28(2)：174－178. Li Yongye, Sun Xihuan, Li Fei, et al. Hydraulic characteristics of transportation of different piped carriages in pipe[J]. Journal of Drainage and Irrigation Machinery Engineering, 2010, 28(2): 174－178. (in Chinese with English abstract)

[12] Lenau C W, El-Bayya M M. Treatment of unsteady flow through capsule pipeline: Capsule-water interaction[J]. Particulate Science and Technology, 1992, 1(92): 215－219.

[13] Barthès-Biesel D. Modeling the motion of capsules in flow[J]. Current Opinion in Colloid & Interface Science, 2011, 16 (1): 3－12.

[14] Vlasak P, Berman V. A contribution to hydro-transport of capsules in bend and inclined pipeline sections[J]. Handbook of Powder Technology, 2001, 10 (1): 521－529.

[15] Kroonenberg H H. A mathematical model for concentric horizontal capsule transport[J]. Canadian Journal of Chemical Engineering, 1978, 56(5): 538－543.

[16] Cheng C C, Liu H. Tilt of stationary capsule in pipe[J]. Journal of Hydraulic Engineering, 1996, 122(2): 90－96.

[17] Zhang X L, Sun X H, Li Y Y. 3-D numerical investigation of the wall-bounded concentric annulus flow around a cylindrical body with a special array of cylinders[J]. Journal of Hydrodynamics, 2015, 27(1): 120－130.

[18] 李永业，孙西欢，许飞. 基于FLOW-3D的筒装料管道水力输送数值模拟[J]. 系统工程理论与实践，2013，33(1)：262－266. Li Yongye, Sun Xihuan, Xu Fei. Numerical simulation on the piped hydraulic transportation of tube-contained raw material based on FLOW-3D[J]. Systems Engineering-Theory & Practice, 2013, 33(1): 262－266. (in Chinese with English abstract)

[19] Khalil M F, Kassab S Z, Adam I G, et al. Turbulent flow around single concentric long capsule in a pipe[J]. Applied Mathematical Modelling, 2010, 34(8): 2000－2017.

[20] Asim T, Mishra R. Computational fluid dynamics based optimal design of hydraulic capsule pipelines transporting cylindrical capsules[J]. Powder Technology, 2016, 55(2): 505－515.

[21] 黄浩钦，刘厚林，王勇，等. 基于流固耦合的船用离心泵转子应力应变及模态研究[J]. 农业工程学报，2014，30(15)：98－105. Huang Haoqin, Liu Houlin, Wang Yong, et al. Stress-strain and modal analysis on rotor of marine centrifugal pump based on fluid-structure interaction[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(15): 98－105. (in Chinese with English abstract)

[22] Gao K, Xie Y H, Zhang D. Effects of stator blade camber and surface viscosity on unsteady flow in axial turbine[J]. Applied Thermal Engineering, 2017, 118(1): 748－764.

[23] 张春晋. 不同直径的管道车在平直管段内运移时的水力特性模拟研究[D]. 太原：太原理工大学，2015. Zhang Chunjin. The Simulation Research on Hydraulic Characteristics of Moving Piped Carriage with Different Diameter at Horizontal Pipeline[D]. Taiyuan: Taiyuan University of Technology, 2015. (in Chinese with English abstract)

[24] 资丹，王福军，陶然，等. 边界层网格尺度对泵站流场计算结果影响研究[J]. 水利学报，2016，47(2)：139－149. Zi Dan, Wang Fujun, Tao Ran, et al. Research for impacts of boundary layer grid scale on flow field simulation results in pumping station[J]. Journal of Hydraulic Engineering, 2016, 47(2): 139－149. (in Chinese with English abstract)

[25] 张春晋，李永业，孙西欢. 明流泄洪洞水力特性的二维数值模拟与试验研究[J]. 长江科学院院报，2016，33(1)：54－60.

[26] Xi W X, Cai, J, Huai X L. Numerical investigation on fluid-solid coupled heat transfer with variable properties in cross-wavy channels using half-wall thickness multi-periodic boundary conditions[J]. International Journal of Heat and Mass Transfer, 2018, 122: 1040－1052.

[27] Yu K, Cheng Y G, Zhang X X. Hydraulic characteristics of a siphon-shaped overflow tower in a long water conveyance system: CFD simulation and analysis[J]. Journal of Hydrodynamics, Ser. B, 2016, 28(4): 564－575.

[28] 张春晋，孙西欢，李永业，等. 螺旋流起旋器内部流场水力特性数值模拟与验证[J]. 农业工程学报，2018，34(1)：53－62. Zhang Chunjin, Sun Xihuan, Li Yongye, et al. Numerical simulation and verification of hydraulic characteristics of internal flow field in spiral flow generator[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(1): 53－62. (in Chinese with English abstract)

[29] 赵晓慧. 基于高速摄像技术的管道车运动特性试验研究巡航导弹锥形头罩分离仿真分析[D]. 长沙：国防科技大学，2009. Zhao Xiaohui. Design and Simulation for the Separation of a Taper Nose Cap from a Cruise Missile[D]. Changsha: National University of Defense Technology, 2009. (in Chinese with English abstract)

[30] 张春晋，孙西欢，李永业，等. 筒装料管道水力输送动边界环状缝隙流水力特性数值模拟[J]. 农业工程学报，2017，33(19)：76－85. Zhang Chunjin, Sun Xihuan, Li Yongye, et al. Numerical simulation of hydraulic characteristics of cyclical slit flow with moving boundary of tube-contained raw materials pipelines hydraulic transportation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(19): 76－85. (in Chinese with English abstract)

Effect of fluid-structure interaction on internal flow field characteristics of tube-contained raw material pipeline hydraulic transportation

Zhang Chunjin1, Sun Xihuan1,2※, Li Yongye1, Zhang Xueqin3, Zhang Xuelan1, Yang Xiaoni1,4, Li Fei1

(1.030024,; 2.030600,; 3.250200,; 4.032300,)

Due to the problems of energy crisis and environmental pollution in the traditional long-distance transportation mode of agricultural products, it has become an inevitable trend to seek a low-carbon and environmentally-friendly transportation mode of agricultural products. In order to further analyze the effect of the fluid-solid interaction on the internal flow field characteristics of the tube-contained raw material pipeline hydraulic transportation, the geometrical model of the tube-contained raw material pipeline hydraulic transportation was established, and the fluid domain within the pipeline and the solid domain of the piped carriage were jointly solved by using a commercial ANSYS Fluent 12.0 software. At the same time, the simulated values obtained by coupling calculation were compared with the experimental values. The unsteady numerical calculation of the fluid domain within the pipeline was based on the Reynolds time-averaged momentum equations and the RNG-turbulent model, and the coupling calculation of the instantaneous speed and displacement of the solid domain for the piped carriage at any time was based on the structural dynamic equations. The tube-contained raw material pipeline hydraulic transportation worked by taking water as transmission medium, sealing agricultural products inside the piped carriage, pushing the piped carriage by using pressurizing devices, and realizing the long distance transport of the piped carriage. This transportation mode had the advantages of low transportation cost, high transportation efficiency and little environmental pollution. The internal flow field characteristics of transporting the piped carriages with a height of 0.1 m and 4 diameter-length ratios of 0.5, 0.6, 0.7 and 0.8 respectively were studied by using the model test. The flow velocity distribution of the typical cross-sections was measured by using the Laser Doppler Anemometry and the photoelectric timing device. The time-average pressure of piezometer tubes was measured by using the standard dynamic pressure collection system and the pressure sensors. The instantaneous speeds and instantaneous displacements of the piped carriages were measured by using the high speed camera. The results showed that the simulated values were in good agreement with the experimental values, which further indicated that it was feasible to adopt the fluid-structure interaction methods to solve the internal flow field characteristics of the tube-contained raw material pipeline hydraulic transportation. As the diameter-length ratio of the piped carriage increased, the affected areas of the axial flow velocity, the radial flow velocity and the pressure gradually increased, the affected areas of the vorticity magnitude gradually decreased, and the affected areas of the circumferential velocity gradually decreased first and then increased near the front end of the piped carriage. The combined effects of both the energy dissipation and the energy conversion caused local low pressure areas to develop near the front end of the piped carriage, but energy conversion caused the downstream pressure of the piped carriage to increase again. The time-average pressure drop coefficients of the piped carriages first decreased and then increased with the increasing of the diameter-length ratio, and the time-average pressure drop coefficient caused by the piped carriage with the diameter-length ratio of 0.7 was the least. During the transport process of the piped carriage along the pipeline, the distributions of the axial velocity, radial velocity, circumferential velocity and vorticity magnitude in the near-wall region of the piped carriage were basically the same, but the pressure distributions showed a gradually decreasing trend. The research in this paper provides an important theoretical reference for the structural design and hydrodynamic mechanism analysis of the piped carriage.

flow fields; pressure; agricultural product; fluid-structure interaction; flow field characteristics; piped carriage; diameter-length ratio; coupling model

10.11975/j.issn.1002-6819.2018.18.037

S229+.1; U173.91

A

1002-6819(2018)-18-0299-09

2018-03-02

2018-08-07

国家自然科学基金项目（51179116，50579044，51109155）；山西省自然科学基金项目（2015011067，201701D221137）

张春晋，山西平遥人，博士生，主要从事流体力学及流体机械研究。Email：zhangchunjintyut@163.com

孙西欢，山西临猗人，博士，教授，博士生导师，主要从事工业水力学研究。Email：sunxihuan@tyut.edu.cn

张春晋，孙西欢，李永业，张学琴，张雪兰，杨小妮，李 飞. 流固耦合作用对筒装料管道车水力输送内部流场特性的影响[J]. 农业工程学报，2018，34(18)：299－307. doi：10.11975/j.issn.1002-6819.2018.18.037 http://www.tcsae.org

Zhang Chunjin, Sun Xihuan, Li Yongye, Zhang Xueqin, Zhang Xuelan, Yang Xiaoni, Li Fei. Effect of fluid-structure interaction on internal flow field characteristics of tube-contained raw material pipeline hydraulic transportation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(18): 299－307. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.18.037 http://www.tcsae.org