振动收获过程中杏果实脱落的动态响应
散鋆龙,杨会民,王学农,郭文松,侯书林※
振动收获过程中杏果实脱落的动态响应
散鋆龙1,杨会民2,王学农2,郭文松1,侯书林1※
(1. 中国农业大学工学院,北京 100083;2. 新疆农业科学院农业机械化研究所,乌鲁木齐 830091)
为研究杏果实脱落不同阶段内的瞬时响应状态与运动状态,该文建立了杏果实-果枝双摆动力学模型,利用双机位高速摄像仪记录果实受迫振动并发生脱落全过程。理论分析与试验表明:杏果实-果枝双摆系统在振动过程中主要表现为果枝摆动、果枝扭转和果实倾摆3种运动状态,果实在空间运动的轨迹接近椭圆形。使用PCC 3.1高速视频控制分析软件获得杏果实在不同平面内相对静止原点的速度、脱落前瞬时速度和加速度数据。试验中不同平面内果实振动脱落速度变化分为3个阶段,通过MATLAB对不同平面内果实相对于静止原点的速度进行傅里叶拟合,得到整体及各阶段速度拟合曲线及相应函数,同时推导出具有完整周期的前2个阶段的速度函数周期与振幅间的关系。通过对比杏果实-果枝实际连接力,分析果实振动脱落特性,为优化杏振动收获机设计参数、提高果实采收率提供理论依据。
振动;采摘;模型;杏;高速摄像;运动分析
0 引 言
利用振动方式对林果进行机械化收获作业是提高整个林果生产率的有效手段之一。自1980年以来,相对于人工采摘,使用机械进行林果收获具有明显的经济优势,利用机械化收获桃子效率可提高3倍[1],采收咖啡豆效率可提高8倍[2]。国外已拥有多种针对不同林果品种的收获机械,并对果树振动收获理论进行了大量的研究。
目前林果机械化大面积收获的研究主要集中在振动参数对收获的影响[3-5]、果树振动响应状态[6-7]和振动能量传递与耗散[8-9]等方面。Láng等[10-13]建立了单自由度果树模型,对果树受到不同惯性式振动激励后的响应状态进行了系统的建模分析。Castro-García 等[14-15]对不同频率、振动时间和振动次数等振动参数对五针松松子机械化收获的影响进行了研究,保证果树嫩枝和树皮所受损伤最小的同时,获得最佳的收获效率。Du等[16-17]对樱桃树施加正弦振动激励,研究主要分枝不同位置的振动响应状态、能量传递与损耗,分析果树分枝节点角度与振动传递间的关系,并对山核桃果树进行3D建模并对振动特性进行了分析[18-20]。
此外,对收获前果实识别与定位的相关研究较多[21-25],但分析果实振动脱落过程与运动状态的分析研究鲜有报道。王春耀等[26]利用高速摄像仪记录二维平面内果实受振动脱落过程,研究果实瞬时运动变化规律,分析果实振动脱落不同阶段运动参数。杜小强等[27-28]借助扁球形电子果实,获得果实受到三维激振收获系统的振动响应,研究分析不同阶段果实所受冲击加速度变化,为果实在振动收获过程中损伤评估和振动机械参数优化提供参考。
完善林果机械化收获理论,研制高效林果收获机械,是加快中国林果产业化发展,降低生产成本的重要途径。本文首次采用双机位高速摄像仪拍摄杏振动收获时果实脱落全过程。研究三维空间内杏果实脱落不同阶段内的瞬时响应状态与运动状态,测量分析果实各项运动参数。建立杏果实-果枝动力学模型,结合振动收获机振动特性,对比果实-果枝实际连接力,分析果实振动脱落特性,以期为优化杏振动收获机设计参数、提高果实收获率提供理论依据。
1 杏果实-果枝动力学模型及求解
1.1 杏果实-果柄动力学模型
杏的实际生长情况相对特殊,果实果柄极短,果柄长度约等于花萼深度,且果实生长方向随机,不同品种杏树果实生长状态不同,主要分为2种形式:果实直接生长在较粗的枝干上(图1a),受迫振动时随枝干运动,生长在较粗枝干的果实分析时果实-果枝可简化视为单摆模型;果实垂吊生长在单独的细长枝干上(图1b),此时细长果枝类似于苹果长果柄,运动过程中果枝也会发生相对摆动,垂吊生长的果实分析时果实-果枝可简化为双摆模型。根据库麦提杏实际生长情况,本文仅对杏果实-果枝双摆模型进行分析和理论推导。

图1 杏果实生长状态
杏果实-果枝双摆模型在受迫振动过程中主要运动状态有3种:果枝摆动、果实相对果枝间的扭转和果实倾摆(图2a)。若忽略果柄和空气阻力对运动的影响,可将果枝视为刚性杆,果实视为球体质心为,以果枝与主枝干连接处为原点,为水平方向,为垂直方向,建立具有3个自由度的双摆模型,如图2b所示。

注:1:果枝带动果实摆动;2:果枝带动果实扭转;3:果实摆动;θ为果枝与垂直方向夹角,(°);φ为果实质心与垂直方向夹角,(°);δ为果实与果枝间的扭转夹角,(°);k0为果实与果枝连接处弹性系数,常数;k1为果枝弹性系数,常数;k2为果实与果枝间扭转弹性系数,常数;l为果枝长度,mm;m1为果枝质量,kg;r为果实半径,mm;m0为果实质量,kg。
杏果实-果枝双摆系统由杏果实速率与转动惯量产生的动能为

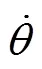
由重力和弹性挠度所产生的势能为

式中为重力加速度,取9.8 m/s2;0为果实与果枝连接处弹性系数,常数;1为果枝弹性系数,常数;2为果实与果枝间扭转弹性系数,常数。
由式(1)动能和式(2)势能可得拉格朗日函数为
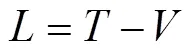
系统Rayleigh耗散函数为
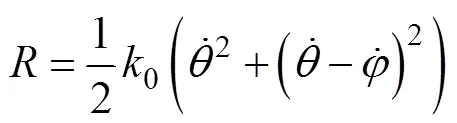
可得保守系统拉格朗日方程

将式(3)带入(5)可得杏果实-果枝双摆系统振动动力学微分方程组为

1.2 杏果实-果枝双摆动力学模型求解
针对杏果实-果枝双摆动力学模型,杏树在受到振动激励后,果实振动规律与“果树-收获机”振动收获系统保持一致,果枝在竖直方向上微幅振动,不考虑果实转动惯量以及Rayleigh耗散,仅考虑果枝在水平方向的振动。
对杏果实-果枝双摆系统非线性方程进行分析,根据Kauderer逼近原理可得夹角逼近方程与、方向位移方程为
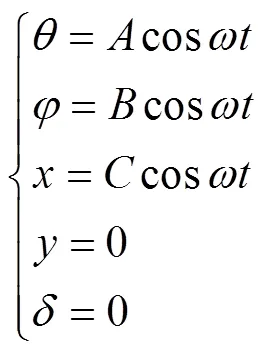
式中为果枝振幅,mm;为果实振幅,mm;为系统振幅,mm;为系统振动角速度,rad/s。

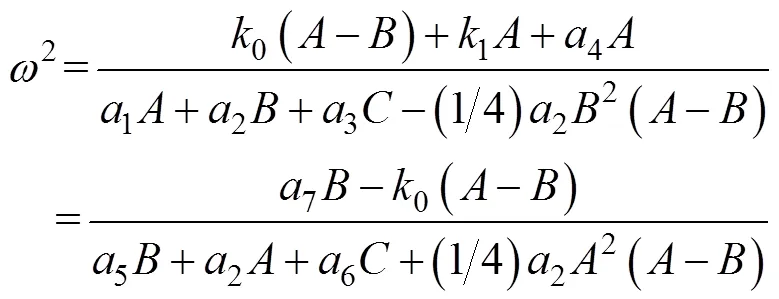


则有

由此可得到系统振动角速度与振型常数间的关系,进而推导出系统频率与振幅间的关系。
1.3 杏果实-果柄分离条件
随着果实的形态学变化和“果实-果枝”系统质量的增加,成熟果实与未成熟果实的振动响应具有差异性,不同生长时期杏果实与果枝间的连接力不同,果实与果柄间连接力随着果实成熟而变小[32]。当机械施加的振动能量沿着果枝传递到果实处,被放大的加速度与果实自身重力形成惯性作用,促使果实产生脱落运动。
由图3二维平面杏果实受力分析可知:当果实-果柄间连接力沿惯性力方向分力与果实自身重力的法向力之和小于惯性力F法向分力时,杏果实发生脱落,即:

注:F为果实与果柄连接力,N;F为果实惯性力,N;F为惯性力法向分力,N;F为惯性力切向分力,N;为果实加速度,m·s-2;a为法向加速度,m·s-2;a为果实加速度,m·s-2。
Note:Fis the connection force between fruit and carpopodium, N;Fis the inertia force, N;Fis the normal force of inertia force, N; Fis the tangential force of inertia force, N;is the acceleration, m·s-2;ais the normal acceleration, m·s-2;ais the tangential acceleration, m·s-2.
图3 杏果实受力分析图
Fig.3 Apricot fruit stress analysis
果实受振动激励产生加速度与自重产生的惯性力F,可分解为果实分离的法向切应力n和产生力矩的切向力F,果实法向加速度和切向加速度分别为a和a。

实际收获过程中,果实分离主要依靠果实惯性力的法向分力F,果实重力沿连接点方向上的分力忽略不计,因此振动收获过程中果实分离力必须满足果实的法向切应力大于果实与果枝沿惯性力法向方向连接力。即

2 杏果实振动脱落试验
为了验证理论分析的正确性,研究杏果实-果枝双摆模型系统在振动采收过程中果实的运动特性以及脱落特性,于2017年6月23日杏成熟期,在新疆巴音郭楞蒙古自治州轮台县新疆农业科学院轮台国家果树资源圃(41°46′56″N, 84°13′22″E)中进行杏果实振动脱落试验。试验果园水肥管理良好,无套种作物,果树种植行距6 m,株距3 m,果树为10 a树龄的库麦提杏树。
2.1 仪器与设备
杏基本参数测量仪器:ATAGO 公司PAL-1型可溶性固形物含量测量仪,测试范围0~53%;华驰HC10002型电子秤,精度0.01 g;上海昂轩仪器公司AM-50型数显式推拉力计和自制夹头测量果实-果柄分离力(如图4),量程0~50 N,精度0.001 N;AY-4型果实硬度计测量果实表面硬度,量程0~50 kg/cm2,精度0.01 kg/cm2。

图4 成熟期杏果实特性参数测量
视频图像设备:美国Vision Research公司Phantom v9.1型高速摄像仪2台,最高分辨率为1 600×1 200,帧频率范围1 000~16 000 Hz; Nikon公司AF 50 mm f/1.8 D全画幅单反镜头,最近对焦距离0.45 m,最大放大倍率0.151倍。
数据分析软件:Phantom Camera Control (PCC) 3.1 高速摄像仪控制与分析软件,MATLAB 2016数据分析软件。
振动装置:选用新疆农业科学院农业机械化研究所研制的4GZG-25型牵引式振动收获机进行果实振动脱落试验,如图5所示。收获机振动部件采用对称双偏心块设计,工作时可稳定输出正弦振动激励,振动频率范围10~15 Hz,振动周期范围0.06~0.1 s,偏心块转速范围500~1 000 r/min,一次作业可完成振动落果、收获、除杂和装箱作业,适用于大型果园收获。

图5 4GZG-25牵引式振动收获机
2.2 杏果实特性参数测定
在试验果树上不同位置随机选择5片区域,每个区域选择20个果实,进行杏果实主要特性参数测定,所有数据测量后取平均值。
测得成熟期库麦提杏果实平均质量为14.26 g;平均外形尺寸为长28.84 mm、宽27.93 mm、厚27.83 mm;成熟果实表面平均硬度为9.17 kg/cm2;成熟果实-果柄平均连接力2.923 N。
2.3 杏果实振动脱落参数采集
选择型号相同的2台高速摄像仪和镜头同时拍摄杏果实振动脱落过程,采集杏果实振动脱落过程图像与数据。安装调试好的高速摄像仪镜头中心线与果实在同一平面上(如图6),距地面1.75 m,间距相等为1.5 m。以果树根部中心为原点,水平地面为平面,垂直地面方向为方向,建立空间坐标系。一号位与二号位摄像仪镜头分别垂直于平面和平面,果实位于两摄像仪视野交点处,果实在2台摄像机中方向数据相同。振动机施加振动激励后,2台摄像仪可拍摄不同平面内果实从开始振动到脱落的全过程,联合可得杏果实空间运动状态。

图6 高速摄像仪机位安放示意图
振动收获前调整镜头焦距,使杏生长区域图像在与高速摄像仪连接的电脑上可清晰显示(图7),对2台摄像机均可见的杏果实进行标记。
选取拍摄区域无遮挡、振动脱落过程无碰撞、不发生干涉的单个杏果实进行图像采集与分析。摄像机拍摄采样频率1 000 fps,时间间隔周期1 000s,曝光度990s,图像分辨率1 280×720。拍摄时间为果实静止到完全脱落,图像相对比例为0.348 mm/pix。
利用PCC 3.1高速视频控制分析软件,得到杏果实受迫振动发生脱落过程视频图像,并导出果实脱落不同阶段在不同平面内的瞬时位移坐标、相对于果实静止时目标点的速度以及瞬时速度数据。利用MATLAB数据处理软件对所有数据进行分析,得到果实在空间上的运动轨迹以及动态数据。

图7 不同位置高速摄像仪拍摄的图像
3 结果与分析
3.1 果实振动脱落运动状态及轨迹分析
利用PCC 3.1高速摄像仪视频分析软件,得到杏果实从受迫振动到发生脱落过程中主要的运动状态图像(如图8所示)。通过对比静止时(图8a)与发生受迫振动过程中(图8b)果枝形态以及观测点位置可知:受破振动过程果实发生了明显的形态变化,果实-果枝整体位置发生明显位移,即果实-果枝发生摆动,果枝发生了扭转运动;观测点相对位置改变,标记果实发生了明显的偏转。对比结果与理论分析中假设的果实运动状态一致。

图8 杏果实-果枝运动状态
由分析软件记录的数据可知,目标果实从开始振动到果实脱落的总时间为0.322 s。以目标果实标记中心为原点,每隔0.002 s对所跟踪的杏果实在平面与平面上的位置坐标进行1次采集,得到目标果实从开始振动到脱落过程中在2个平面上的轨迹坐标数据,整合后绘制杏果实三维空间运动轨迹曲线。
由图9杏果实空间运动轨迹可知:杏果实从振动到脱落前,整个空间运动轨迹近似椭圆形。结果与Cooke和Rand[29-31]推导得出的果实-果柄动力运动学轨迹的结论一致。
3.2 果实脱落运动参数分析
以果实静止时标记中心为目标原点,研究果实振动脱落过程中的运动状态,分析在不同平面上果实振动脱落过程中每0.002 s时间间隔内相对于原点的速度的变化规律,即受迫振动后杏果实相对原点速度()与时间的关系。同时,利用PCC 3.1软件测量果实脱落时瞬时速度,获得果实脱落前加速度,进而推导出果实在不同平面上的受力。

图9 杏果实空间运动轨迹
3.2.1 杏果实在平面内运动状态
利用MATLAB对目标果实在平面速度与加速度数据进行拟合分析可知,目标果实受迫产生振动至脱落过程中相对果实静止点速度符合傅里叶变换形式,相对果实静止位置的速度拟合曲线如图10所示。
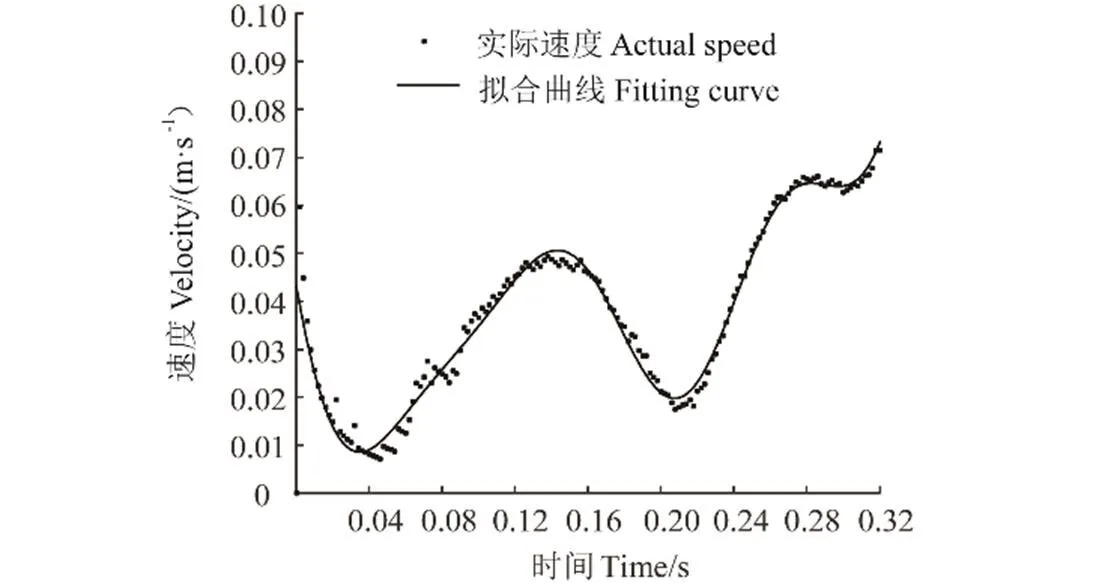
图10 杏果实在xoz平面上速度拟合曲线
杏果实在平面上速度的傅里叶拟合曲线2为0.970 4,其拟合函数方程为

式中为时间,s。
通过对高速摄像仪拍摄杏运动图像和数据分析,由平面上相对原点的速度与时间的傅里叶函数拟合曲线图10可知,果实发生脱落时最大速度为0.112 m/s,果实在平面上从开始振动到脱落速度变化共经历的3个阶段:0至0.148 s、0.148至0.248 s和0.248至0.322 s。果实在第3阶段未达到完整周期就已脱落,为保证分析准确性,仅对具有完整振动周期的第1阶段和第2阶段的数据进行对比分析。
杏果实在平面上第1阶段的速度与时间的傅里叶拟合函数曲线如图11a所示,2为0.965 2,周期为0.15 s。拟合方程为

杏果实在平面上第2阶段的速度与时间的傅里叶拟合函数曲线如图11b所示,2为0.952 5,周期为0.15 s。拟合方程为

通过分析傅里叶拟合曲线图11可知:果实速度在第1和第2阶段内速度均呈现周期性变化,速度变化周期为0.15 s;前2个阶段速度函数振幅均为0.021 m/s。

图11 杏果实在xoz平面上第1和第2阶段速度拟合曲线
利用PCC 3.1软件所得测量数据,杏果实在平面上,果实脱落前0.002 s与脱落时刻间相对速度为1.53 m/s,则此时观测点的加速度为765 m/s2。根据牛顿第二定理,结合成熟果实平均质量,计算可知,0.188 s时果实加速度产生的分离力达到成熟果实-果枝连接力;果实脱落时刻在平面上由加速度产生的分离力为11.22 N。
3.2.2 杏果实在平面内运动状态
利用相同的方法对目标果实在平面速度数据进行拟合分析可知,相对果实静止原点的速度与时间的傅里叶拟合曲线如图12所示。

图12 杏果实在yoz平面上速度拟合曲线
杏果实在平面上速度的傅里叶拟合曲线2为0.986,其函数方程为

由平面上相对原点速度与时间的傅里叶函数拟合曲线图12可知,杏果实在平面上相对原点速度的变化也分为与在平面上相同的3个阶段。果实发生脱落时最大速度为0.166 m/s,果实在第3阶段未达到完整周期就已脱落,为保证分析准确性,仅对第1和第2阶段数据进行对比分析。
对平面上运动的前2个时间相对原点速度数据段进行分析可知:
第1阶段0至0.148 s,傅里叶拟合函数2为0.954 5,周期为0.13 s,振幅为0.027 m/s。拟合曲线如13a所示,拟合函数方程为

第2阶段0.148至0.248 s,傅里叶拟合函数2为0.981 1,周期为0.13 s,振幅为0.054 m/s。拟合曲线如图13b所示,拟合曲线方程为
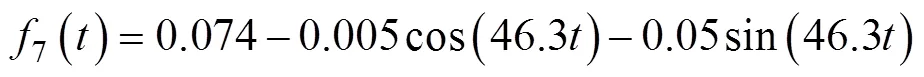

图13 杏果实在yoz平面上第1和第2阶段速度拟合曲线
分析傅里叶拟合曲线图13可知:在平面上杏果实相对原点速度在第1和第2阶段内均呈现周期性变化,速度变化周期为0.13 s;第1阶段速度函数振幅为0.027 m/s,第2阶段速度函数振幅为0.054 m/s。
利用PCC 3.1软件测得数据测得在平面上,脱落前0.002 s与脱落时刻间瞬时速度为1.359 m/s,则此时观测点的加速度为679.98 m/s2。由牛顿第二定理与成熟果实平均质量计算可知:0.154 s时杏果实加速度产生的分离力达到成熟果实-果枝连接力;杏果实脱落时刻在平面上由加速度产生的分离力为9.7 N。
4 结 论
1)建立了三自由度杏果实-果枝双摆模型,并对动力学模型进行分析和求解,明确振动收获中杏果实-果柄系统中各运动参数间关系;对杏果实-果枝双摆系统果实脱落条件进行了理论分析。
2)利用双机位高速摄像仪及分析软件杏果实振动脱落过程进行视频图像采集。目标杏果实脱落过程时间为0.322 s,通过果实振动过程空间坐标,绘制杏果实振动脱落空间运动轨迹,分析可知杏果实-果枝系统在受迫振动后整个空间运动轨迹近似椭圆形。
3)利用PCC 3.1分析软件对与两个平面内同一目标果实进行运动数据采集,可得果实脱落时相对静止原点最大速度分量分别为0.112和0.166 m/s;脱落时刻瞬时加速度分别为765和679.98 m/s2;结合成熟杏果实重量计算得到加速度在各平面上产生的脱落力分量分别为11.22和9.7 N,均大于成熟杏果实与果柄间的平均连接力。
4)利用MATLAB对采集的速度数据进行拟合分析,得到了目标果实在与平面内的傅里叶拟合曲线与拟合函数,其2值分别为0.970 4和0.986。
5)分析果实振动脱落速度拟合曲线可知,果实振动脱落可分为0~0.148 s、0.148~0.248 s和0.248 ~0.322 s三个阶段。果实在第3阶段未达到完整周期就已脱落,为保证分析的准确性,对具有完整周期的第1与第2阶段数据进行分析可知:平面内,前2个阶段速度拟合函数2分别为0.965 2和0.952 5,速度变化周期均为0.15 s,函数振幅均为0.021 m/s;平面内前2个阶段速度拟合函数2分别为0.954 5和0.981 1,速度变化周期均为0.13 s,第2阶段函数振幅是第1阶段的2倍,分别为0.054和 0.027 m/s。杏果实-果枝双摆系统振动周期接近激振源周期。
[1] Torregrosa A. Martin B, Garcia Brunton J, Bernad J J. Mechanical harvesting of processed peaches [J]. Transactions of the ASAE, 2008, 24(6): 723-729.
[2] Filho G R D S, Vieira H D, Rodrigues W P, et al. Comparison between manual and semi-mechanical harvest of coffee fruit in mountainous areas[J]. African Journal of Agricultural Research, 2015, 10(28): 2724-2730.
[3] Torregrosa A, Chaparro O, Ortiz C, et al. Design, construction and testing of an apricot tractor-trailed harvester[J]. Spanish Journal of Agricultural Research, 2008, 3(3): 333-340.
[4] Aristizábal I D, Oliveros C E, Alvarez F. Mechanical harvest of coffee applying circular and multidirectional vibrations[J]. Transactions of the Asae, 2003, 46(2): 205-210.
[5] Erdoǧan D, Güner M, Dursun E, et al. Mechanical harvesting of apricots[J]. Biosystems Engineering, 2003, 85(1): 19-28.
[6] Whitney J D, Churchill D B, Hedden S L, et al. Trunk shakers of citrus harvesting. Part I: Measured trunk shaker and tree trunk motion [J]. Applied Engineering in Agriculture, 1988, 4(2): 93-101
[7] Whitney J D. Smerage G H. Block W A. Dynamic analysis of a trunk shaker-post system [J]. Transactions of the ASAE, 1990, 33(4): 1066-1070
[8] Horvath E, Sitkei G. Damping properties of plum trees shaken at their trunks [J]. Transactions of the ASAE, 2005,48(1): 19-25.
[9] Horvath E, Sitkei G. Energy consumption of selected tree shakers under different operational conditions [J]. Journal of Agricultural Engineering Research, 2001, 80(2): 191-199.
[10] Láng Z. One degree of freedom damped fruit tree model[J]. Agricultural Engineering International Cigr Journal, 2008, 51(3): 823-829.
[11] Láng Z. Dynamic modelling structure of a fruit tree for inertial shaker system design[J]. Biosystems Engineering, 2006, 93(1): 35-44.
[12] Láng Z. A fruit tree stability model for static and dynamic loading[J]. Biosystems Engineering, 2003, 85(4): 461-466.
[13] Láng Z, Csorba L. Modelling and comparing two canopy shapes using FEM[J]. International Journal of Horticultural Science, 2003.
[14] Castro-García S, Blanco-Roldán G L, Gil-Ribes J A. Vibrational and operational parameters in mechanical cone harvesting of stone pine (Pinus pinea L.)[J]. Biosystems Engineering, 2012, 112(4): 352-358.
[15] Castro-García S, Blanco-Roldán G L, Gil-Ribes J A. Vibrational and operational parameters in mechanical cone harvesting of stone pine (Pinus pinea L.)[J]. Biosystems Engineering, 2012, 112(4): 352-358.
[16] Du X,Chen D,Zhang Q, et al. Dynamic responses of sweet cherry trees under vibratory excitations[J]. Biosystems Engineering, 2012, 111(3): 305-314.
[17] Du X, Chen D, Zhang Q, et al Dynamic response of sweet cherry tree to oscillating excitations for mechanical harvest[J]. IFAC Proceedings Volumes, 2010, 43(26): 83-88.
[18] He L,Du X,Qiu G,Wu C.3D Reconstruction of Chinese Hickory Trees for Mechanical Harvest[C]//American Society of Agricultural and Biological Engineers Annual International Meeting-ASABE 2012.
[19] Wu C, He L, Du X, et al. 3D reconstruction of Chinese hickory tree for dynamics analysis[J]. Biosystems Engineering, 2014, 119(1): 69-79.
[20] Du X Q, Wu C Y, He L Y, et al. Dynamic characteristics of dwarf Chinese hickory trees under impact excitations for mechanical fruit harvesting[J]. International Journal of Agricultural & Biological Engineering, 2015, 8(1): 17-25.
[21] Thendral R, Suhasini A, Senthil N. A comparative analysis of edge and color based segmentation for orange fruit recognition[C]. International Conference on Communications and Signal Processing. IEEE, 2014: 463-466.
[22] Li D, Zhang L, Liu Y. A Study on Recognition Method of Fruits Based on Machine Vision[J]. Journal of Software Engineering, 2010, 9(4): 895-902.
[23] Villibor G P, Santos F L, Queiroz D M D, et al. Determination of modal properties, of the coffee fruit-stem system, using high speed digital video and digital image processing[J]. Acta Scientiarum Technology, 2016, 38(1): 41.
[24] 吕继东,赵德安,姬伟,等采摘机器人振荡果实动态识别[J].农业机械学报,2012,43(05):173-178+196. Lü Jidong, Zhao De’an, Ji wei, et al. Dynamic recognition of oscillating fruit for harvesting robot[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(5): 173-178+196.
[25] 吕继东,赵德安,姬伟. 采摘机器人振荡果实匹配动态识别[J]. 农业工程学报,2013,29(20):32-39. Lü Jidong, Zhao De’an, Ji Wei. Research on matching recognition method of oscillating fruit for apple harvesting robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE) 2013, 29(20): 32-39. (in Chinese with English abstract)
[26] 蔡菲,王春耀,王学农,等. 基于高速摄像技术的振动落果惯性力研究[J].西北农林科技大学学报(自然科学版),2013,41(04):208-212. Cai Fei, Wang Chunyao, Wang Xuenong, et al. Inertia force of fruits abscised by vibration based on high-speed video camera technology[J]. Journal of Northwest A&F University (Nat. Sci. Ed), 2013,41(04): 208-212. (in Chinese with English abstract)
[27] 杜小强,李松涛,贺磊盈,等. 三维激振果品采收机构优化设计与试验[J]. 农业工程学报,2017,33(16):48-55. Du Xiaoqiang, Li Songtao, He Leiying, et al. Optimal design and experiment on vibratory fruit harvesting mechanism with three-dimensional excitation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(16): 48-55. (in Chinese with English abstract)
[28] 杜小强,李党伟,贺磊盈,等. 基于电子果实技术的机械振动采收过程果实运动分析[J]. 农业工程学报,2017,33(17):58-64. Du Xiaoqiang, Li Dangwei, He Leiying, et al. Fruit motion analysis in process of mechanical vibration harvesting based on electronic fruit technique[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(17): 58-64. (in Chinese with English abstract)
[29] Crooke J R, Rand R H. Vibratory fruit harvesting: A linear theory of fruit-stem dynamics[J]. Journal of Agricultural Engineering Research, 1969, 14(3): 201-200.
[30] Rand R H, Cooke J R. Vibratory fruit harvesting: A non-linear theory of fruit-stem dynamics [J]. Journal of Agricultural Engineering Research, 1970, 15(4): 357-356.
[31] Parchomchuk P, Cooke J R. Vibratory harvesting: an experimental analysis of fruit-stem dynamics[J]. Theoretical Computer Science, 1972, 40(12): 131-148.
[32] 散鋆龙,刘旋峰,牛长河,等. 杏果实成熟度特性参数与果柄分离力的相关性分析[J]. 农业工程学报,2013,29(23):62-68. San Yunlong, Liu Xuanfeng, Niu Changhe, et al. Relativity analysis between characteristic parameters of apricot’s ripeness and its fruit removal force[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(23): 62-68. (in Chinese with English abstract)
Dynamic response analysis of apricot fruit dropping during vibration harvesting
San Yunlong1, Yang Huimin2, Wang Xuenong2, Guo Wensong1, Hou Shulin1※
(1.100083; 2.830091)
In order to study the transient response state and movement state of apricot fruit during different stages of exfoliation, a dynamic model of apricot fruit-fruit branch double pendulum hanging on a single long stem branch according to the actual growth of apricot fruit was established in this paper. The apricot fruit-stem separation conditions were analyzed theoretically, and the physical parameters of Kumai apricot fruit at ripening stage were measured. The whole forced vibration process of the target fruitS was recorded by using 2 high-speed cameras with same specifications perpendicular to theplane and theplane, and the relevant datas such as shedding time, speed, and acceleration were obtained. Theoretical analysis and experiments showed that the apricot fruit-fruit branch double pendulum system mainly shows 3 kinds of motion states: fruit branch drives fruit to swing, fruit branch drives fruit to twist and fruit swing. The average weight of the ripe fruit of Kumari apricot was 14.26 g, the average external dimensions were 28.84 mm in length, 27.93 mm in width, and 27.83 mm in thickness; the average surface hardness of mature fruit was 9.17 kg/cm2; and the average connection force of ripe fruit-stem is 2.923 N. Based on the measured spatial coordinates of the fruit in theandplanes and Phantom Camera Control 3.1 high-speed video control software analysis, the whole spatial motion track of apricot fruit is nearly elliptical from vibration to shedding, the total time from vibration to shedding of target fruit was 0.322 s, and the maximum speed of the relative static origin of apricot fruit was 0.112 and 0.166 m/s when be dropped in spatial planesand. The instantaneous speed of the apricot fruit before shedding was 1.53 and 1.359 m/s, respectively, and the acceleration was 765 and 679.98 m/s2, respectively. Using MATLAB software, the velocity data of fruit in different planesandwere compared with the Fourier fitting curves of velocity and time relative to stationary origin, and the fitting curve of the speed of apricot fruit during vibration shedding and the corresponding function were obtained.2value of the fitting function were 0.970 4 and 0.986. Through analyzing the speed function curve, the process of fruit vibration shedding could be divided into 3 periods: 0 to 0.148 s, 0.148 to 0.248 s, and 0.248 to 0.322 s. In the third stage, the fruit has already fallen off before it reaches the full cycle. To ensure the accuracy of the analysis, the analysis of the velocity function in the first 2 stages with complete vibration period showed that: in theplane, the velocity fitting function2of the first 2 stages are 0.965 2 and 0.952 5, respectively, the speed change period is 0.15 s and the function amplitude is 0.021 m/s; the velocity fitting function2in the first 2 stages of theplane is 0.954 5 and 0.981 1, respectively, and the speed change period is 0.13 s, the amplitude of the second stage function is twice that of the first stage, which is 0.054 and 0.027 m/s, respectively. The vibration cycle of the apricot fruit-fruit branch double pendulum system is close to the period of the excitation cycle. According to the calculation of the fruit weight of mature apricot, the shedding force components produced by acceleration on each plane were 11.22 and 9.7 N respectively, both of which were greater than the average connected force between mature apricot fruit and stalk. Based on the above characteristics of fruit vibratory shedding, this study can provide a theoretical basis for clarifying the shedding mechanism during fruit harvesting, optimizing the design parameters of apricot vibrating harvester, and improving the fruit recovery rate.
vibration; picking; models; apricot; high-speed camera; motion analysis
10.11975/j.issn.1002-6819.2018.18.009
S225.93
A
1002-6819(2018)-18-0068-08
2018-05-22
2018-07-27
国家自然科学基金项目—新疆杏振动脱落动力学特性及振动采收机理研究(51465059)
散鋆龙,男,博士生,从事机械制造及自动化研究。 Email:sanyunlong@hotmail.com
侯书林,教授,博士生导师,主要从事机械设计及制造工艺研究。Email:hsl010@126.com
散鋆龙,杨会民,王学农,郭文松,侯书林. 振动收获过程中杏果实脱落的动态响应[J]. 农业工程学报,2018,34(18):68-75. doi:10.11975/j.issn.1002-6819.2018.18.009 http://www.tcsae.org
San Yunlong, Yang Huimin, Wang Xuenong, Guo Wensong, Hou Shulin. Dynamic response analysis of apricot fruit dropping during vibration harvesting [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(18): 68-75. (in Chinese with English abstract) doi: 10.11975/j.issn.1002-6819.2018.18.009 http://www.tcsae.org

