基于介电功能梯度材料的盆式绝缘子电场分布优化

孙秋芹 郭晓和 张永涛 汪沨 陈赦 罗宸江 杨德慈

摘 要：为改善盆式绝缘子沿面电场分布，以径向介电常数分布为对象，提出了一种通过识别沿面最大场强位置反馈更新介电常数分布的全局优化算法，实现了介电功能梯度材料盆式绝缘子参数优化设计.通过APDL语言，实现MATLAB与ANSYS联合仿真，研究了步长大小、分层数量等参数对优化结果的影响.结果表明：随着步长减小，沿面场强分布随迭代次数的变化更加平滑，介电常数区间范围增大.分层数目越多，径向介电常数分布越平滑，高压端介电常数值越大，沿面电场分布波动越小，最大场强降低幅度越大，可达70.5%.盆式绝缘子场强集中区域从高、低电极和三结合点处往中间转移，上、下表面电场利用率均达到0.75以上.研究结果为盆式绝缘子优化设计提供了参考.

关键词：盆式绝缘子；介电功能梯度材料；步长；分层数量；沿面电场利用率

中图分类号：TM854 文献标志码：A

Abstract：In this work， the dielectric functionally graded material （εFGM） was initially employed to improve the electric field distribution along spacer surface. Taking the permittivity distribution as the object， a global optimization algorithm was proposed in this paper， which usesd the maximum electric stress as a feedback to update the permittivity distribution. Using the APDL language incorporated in ANSYS combined with MATLAB， the influences of step length and layer number on the field were studied. The results show that the electric stress along spacer surface becomes smoother with the decrease of step length and the increase of iteration number. Correspondingly， the permittivity range is significantly enlarged. The high electric field area of spacer is shifted from the electrode and triple junction to the middle part， and the utilization ratio along the lower and upper surface reaches 0.75. The results provide useful references for spacer design.

Key words：spacers；dielectric functionally graded material；step length；layer number；utilization rate of surface electric field

气体绝缘金属封闭开关设备（GIS）具有占地面积小、运行可靠、维护方便等特点，在电力系统中获得了广泛应用.随着电压等级的提升和系统容量的不断增大，GIS设备逐渐趋于小型化，设备故障量迅速增多.盆式绝缘子在GIS中起着支撑导体、隔离气室和电气绝缘的作用，是GIS中最薄弱的环节[1].统计数据表明，盆式绝缘子沿面放电在GIS故障中占有相当大的比例[2].

为改善盆式绝缘子沿面电场分布，降低沿面放电和击穿的概率，通常采用形状优化的方式来实现.该措施常使得盆式绝缘子结构异常复杂且制造困难.功能梯度材料（Functionally Graded Materials，FGM）最早由日本学者提出，它由两种或两种以上材料通过物理或化学方法复合而成，构成材料的要素可沿特定方向由一侧向另一侧连续变化，从而使得材料的性质和功能呈现梯度变化[3].介电功能梯度材料（εFGM）的出现为盆式绝缘子电场优化提供了新的途径，仅需通过对材料介电常数进行调制，即可达到优化电场的目的.

近年来国内外学者针对εFGM开展了探索研究.文献[4-5]制作了径向介电常数呈U型分布的盆式绝缘子，并进行了实验，有效降低了高、低压电极交界面处的场强；文献[6]综合考虑绝缘子高压端优化区域尺寸与介电常数取值得到优化的介电常数分布，降低了三结合点处场强，提高了击穿电压；文献[7]为降低三结合点处场强，对不同的介电常数递减方案进行了对比，结果表明，径向介电常数分布先线性递减后保持为常数的分布方案，其电场优化效果最佳；文献[8]采用一种逐次逼近算法对盘式、盆式、台式等式样绝缘子的参数分布进行了优化，研究了缩减系数、叠层数以及ε调节范围等参数对优化效果的影响；文献[9]引入了拓扑优化的概念，对台式绝缘子二维空间中介电常数分布进行优化时，最大介电常数取100时，三结合点处场强降幅达到42%；文献[10]将台式绝缘子划分成不同的三角形区域，采用权重线性递减粒子群算法对εFGM台式绝缘子各个区域介电常数的取值进行优化，电场利用因子从0.39提高到0.61.目前，盆式绝缘子介电常数分布的有效优化算法仍较少.本文基于ANSYS与MATLAB联合仿真，提出了一种通用的绝缘子介电常数分布全局优化算法，详细介绍了算法的实现流程，分析了步长大小、分層数量对优化效果的影响，完成了介电常数分布的优化设计.

1 优化原理

1.1 介电功能梯度材料

功能梯度材料是在物料特性确定的前提下，通过材料组成的渐变，如调节不同区域填充材料的体积百分数，带来材料性能的梯度变化，进而实现多种特殊功能，如应力缓和、生物相容、能量调控等的先进材料[11].目前，介电功能梯度材料通常采用离心铸造法、3D打印、叠层法等进行制备[12].采用熔融堆积成形3D打印工艺，通过逐点或逐层地累积形成制件.日本名古屋大学已制造出旋转轴垂直方向上介电常数呈U形分布的FGM，介电常数的区间范围分别为3.8～12.0、5.1～8.6等，其原理如图1所示.通过调节离心力的大小、作用时间、填充颗粒（TiO2、SiO2、Al2O3等），可在离心力方向上得到所需的介电常数分布.

盆式绝缘子为同轴电极结构，电场分布也有类似的规律.当盆式绝缘子与SF6的交界面不与电极表面垂直时，位于介质交界面与电极表面夹角<90°的一侧，介电常数较小的介质中等位线出现压缩现象，电场强度较高[1].

2 仿真模型

工程中盆式绝缘子形状各异，受电压等级等影响，无统一的模型和尺寸，为便于比较分析，参照国内外相关参数，考虑到盆式绝缘子为轴对称结构，以其轴向截面为研究对象，忽略法兰、密封槽、屏蔽环等的影响，本文建立了FGM盆式绝缘子简化仿真模型，如图4所示[5，7].高压导体半径40 mm，盆式绝缘子最大半径100 mm，轴向厚度30 mm.

运用有限元分析软件ANSYS 16.0进行电场数值计算时[15]，建立模型、设置材料属性、网格剖分、设置载荷，最后求解并进行相应的后处理.模型中盆式绝缘子沿径向均匀分成N层（N分别取为10、20、40），每层绝缘子的介电常数可以在一定范围内变化.SF6环境所在区域的介电常数设置为1.0.考虑到工程实际，盆式绝缘子各层介电常数最小值设定为4.0，最大值由仿真计算决定.

本文采用ANSYS参数化设计语言APDL编写程序，在ANSYS中给模型添加轴对称属性，以区别于二维模型.模型单元类型选用PLANE121单元，为8节点、2D、自由度为电场分析单元.网格划分采用用户控制的剖分方法：盆式绝缘子单元大小为0.75 mm，形状为四边形，映射网格划分；SF6环境单元大小为1.5 mm，形状为三角形，自由网格划分.在工频及雷电冲击电压下，电极间电压随时间的变化比较缓慢，极间的绝缘距离比电磁波的波长小得多，介质电场可采用准静态近似，若进一步忽略电导的影响，则可将介质电场等效为静电场[8].将载荷施加在高、低压端的线段上，高压端施加电压为100 kV，低压端施加电压为零.盆式绝缘子上、下表面场强分布如图5所示.

由图5可知，当径向距离为40～55 mm时，上表面电场强度高于下表面，盆式绝缘子上表面三结合点处（高压端-绝缘子-SF6环境）场强最大值为6 122.0 V/mm；径向距离为55～100 mm时，盆式绝缘子下表面电场强度略高于上表面，盆式绝缘子下表面场强最大值在低压端三结合点处取得，场强大小为2 545.64 V/mm.将盆式绝缘子沿径向均匀分为20层，各分层沿面最大场强分布呈不规则U形.

3 优化流程

盆式绝缘子表面电场畸变和局部电场集中是引起盆式绝缘子闪络的主要原因.本文以降低εFGM盆式绝缘子沿面最大场强Ef.max，提高绝缘子上、下表面电场分布均匀度为优化目标，以绝缘子各分层介电常数的取值为优化变量，通过对绝缘子沿面最大场强所在位置的识别，更新介电常数分布.整个优化过程采用MATLAB与ANSYS联合仿真来实现：

1）MATLAB命令调用ANSYS运行.

MATLAB调用ANSYS运行的命令如下[16]：！D：＼＼ ANSYS＼＼ANSYS Inc＼＼v160＼＼ANSYS＼＼bin＼＼winx64＼＼ansys16 0.exep ane3fl dir “F：＼＼Program Files” j “basintype” s read l enus b i “F：＼＼Program Files＼＼main.txt” o “F：＼＼Program Files＼＼ROCORD.txt”.

其中，p表示指定license，ane3fl表明采用的license为ANSYS Multiphysics；b表示采用ANSYS batch模式；j 表示job名称，命名为basintype；i表示输入文件，此处为main.txt文本；o表示输出文件.

此外，ANSYS与MATLAB之间还通过存储介电常数分布的文本dielectric.txt、上表面场强分布的文本upper.txt、下表面电场分布的文本lower.txt进行数据交换.

2）介电常数分布优化模块.由软件MATLAB判断出盆式绝缘子沿面路径上最大场强Ef.max所在的位置（绝缘子第i层），将该层绝缘子的介电常数增加一个步长Δε，不断循环上述操作至最大迭代次数.介电常数优化过程中，软件MATLAB完成盆式絕缘子各分层沿面最大场强的提取与比较、介电常数分布的更新以及沿面最大场强的记录工作，供后续使用.

3）盆式绝缘子电场计算模块.MATLAB命令调用ANSYS以后台执行模式运行，执行相同路径下的命令文件main.txt，完成εFGM盆式绝缘子电场数值计算.执行过程中未启动GUI界面，可以缩短运算时间.此外，ANSYS还参与介电常数分布数据的读取、绝缘子上下表面电场分布数据的写出.

εFGM盆式绝缘子介电常数整体优化流程如图6所示.

4 结果分析

4.1 步长大小

为研究步长大小对优化结果的影响，Δε分别取2.0、1.0、0.5、0.2.算法迭代次数应能保证Ef.max收敛，以及不同步长Δε下介电常数的改变总量相同（假设Δε取0.2时，算法迭代400次，介电常数变化总量为80；当则Δε为0.5时，算法迭代160次；其他情况以此类推）.不同步长下εFGM盆式绝缘子沿面最大场强Ef.max随迭代次数的变化如图7所示.

由图7可知，当步长Δε较大时，随着迭代次数的增加，Ef.max虽整体呈现下降趋势，但在迭代过程中出现较大的波动.优化仿真过程中，第i层绝缘子可能会出现介电常数过度优化的问题，最终得到的介电常数分布与最优分布有较大偏差.减小步长Δε的取值，Ef.max迭代曲线较为平滑.且随着步长的减小，介电常数的改变总量有所增加，介电常数分布更加接近最优分布，不同步长Δε下介电常数分布的优化结果如表1所示.

不同步长下Ef.max降低幅度均达到60%以上，步长越小，优化效果越佳.当步长过小时，迭代次数、仿真时间也要相应地增加.在保证优化效果的前提下为了增加优化效率，后续优化计算中步长Δε的取值固定为0.5.

4.2 分层数量

将盆式绝缘子沿径向均匀分为10层、20层、40层，研究分层数量对优化结果的影响.在研究步长大小对优化效果的影响时，介电常数的改变总量由迭代次数决定，而在研究分层数量对优化结果的影响时，分层数量决定了介电常数的改变总量.此时，由于步长Δε是固定的，迭代次数随分层数量的增加而增加.例如，绝缘子模型分10层时，迭代160次；模型分為20层、40层时，迭代次数分别为320次、640次.不同分层下εFGM盆式绝缘子径向介电常数分布结果如图8所示.

随着盆式绝缘子分层数量的增加，其径向介电常数分布更加平滑，高压端绝缘子介电常数的取值也越大.径向介电常数分布呈现不规则的U形，与图5中盆式绝缘子各分层Ef.max的分布相似，证明了优化结果的合理性.

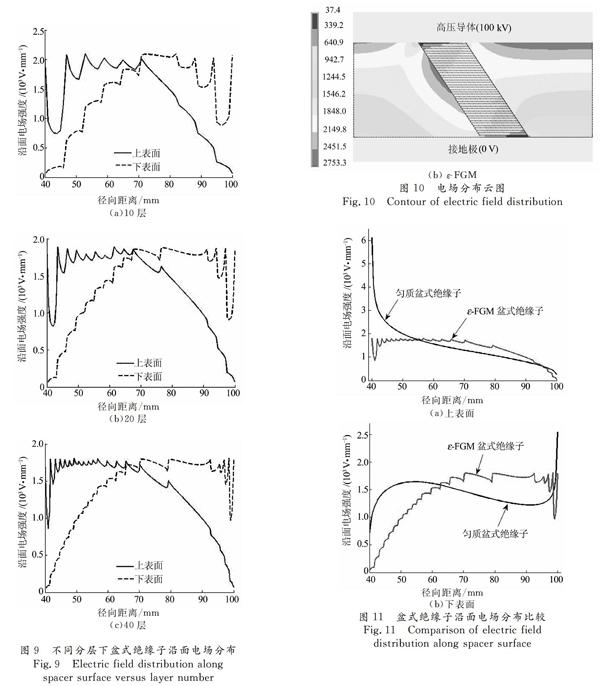
不同分层数目下，盆式绝缘子上、下表面电场分布的优化结果如图9所示.

由图9可知，随着分层数量的增加，Ef.max的降幅增大，沿面电场分布的波动不断减小，介电常数分界面上电场集中现象得到改善.当分层数量分别为0层、20层、40层时，对应沿面最大场强分别为2 100.1 V/mm、1 893.6 V/mm、1 807.9 V/mm.

4.3 电场分布

选择分层数量为40层的εFGM盆式绝缘子，将其沿面电场分布与匀质盆式绝缘子相比较，结果分别如图10、图11所示.

与匀质绝缘子相比较，介电功能梯度材料绝缘子沿面最大场强从6 122.0 V/mm降低到1 807.9 V/mm，降幅达70.5%.εFGM盆式绝缘子三结合点处的电场增强效应被整体的电场平均效应抵消，场强集中区域从高、低压端三结合点处往盆式绝缘子中部转移.现有盆式绝缘子设计过程中，沿面电场控制值位于数千伏/毫米至十千伏/毫米区间范围，取决于电压类型、电压等级、SF6气体压强[17].采用εFGM可有效提高盆式绝缘子可靠性.定义盆式绝缘子沿面场强平均值与最大值的比值为沿面电场利用率，统计结果如表3所示.优化后的εFGM盆式绝缘子上、下表面电场利用率均达到0.75以上，电场畸变严重的上表面电场利用率从0.24提高到0.77，盆式绝缘子沿面电场分布的均匀度显著升高.

5 结 论

本文将同轴圆柱体结构电介质的电场分布优化方法推广到喇叭形结构电介质，通过APDL语言，实现MATLAB与ANSYS联合仿真，提出了一种介电常数分布全局优化算法，涉及变量少、优化效率高，针对性强.通过对εFGM盆式绝缘子径向介电常数分布进行优化研究，得到如下结论：

1）步长较小时，盆式绝缘子沿面最大场强随迭代次数变化的波动减小，避免单层绝缘子介电常数出现过度优化的问题，径向介电常数分布将趋于最优分布.较小的步长会增加介电常数改变总量，算法迭代次数相应增加.

2）盆式绝缘子分层数量越多，高压端绝缘子介电常数的取值越大，介电常数分布越平滑；随着分层数量的增加，绝缘子沿面电场分布波动减小，沿面最大场强降低幅度增大，最大降幅达到70.5%.

3）优化后的εFGM盆式绝缘子场强集中区域从高、低压端三结合点处往绝缘子中部转移，电场畸变严重的上表面电场利用率从0.24提高到0.77.

参考文献

[1] 杜进桥，张施令，李乃一，等.特高压交流盆式绝缘子电场分布计算及屏蔽罩结构优化[J].高电压技术，2013，39（12）：3037-3043.

DU J Q，ZHANG S L，LI N Y，et al.Electric field distribution calculation and shielding electrode structure optimization of UHVAC basintype insulator[J].High Voltage Engineering，2013，39（12）： 3037-3043.（In Chinese）

[2] 刘洪正.高压组合电器[M].北京： 中国电力出版社，2014： 194 -196.

LIU H Z.High voltage combiner[M].Beijing：China Power Press，2014： 194 -196.（In Chinese）

[3] 闫晓磊，钟志华，查云飞，等.功能梯度材料飞轮转子优化设计[J].机械工程学报，2011，47（2）： 72-73.

YAN X L，ZHONG Z H，ZHA Y F，et al.Optimum design of flywheel rotor made of functionally graded materials[J].Journal of Mechanical Engineering，2011，47（2）： 72-73.（In Chinese）

[4] KURIMOTO M，KAI A，KATO K，et al.Fabrication of permittivity graded materials for reducing electric stress on electrode surface[C]// Electrical Insulation，2008.ISEI 2008.Conference Record of the 2008 IEEE International Symposium on.IEEE，2008：265-268.

[5] KURIMOTO M，KATO K，HANAI M，et al.Application of functionally graded material for reducing electric field on electrode and spacer interface[J].IEEE Transactions on Dielectrics and Electrical Insulation，2010，17（1）：256-263.

[6] KATO K，KURIMOTO M，ADACHI H，et al.Impulse breakdown characteristics of permittivity graded solid spacer in SF6[C]// 2001 Annual Report.Conference on Electrical Insulation and Dielectric Phenomena. Kichener：IEEE，2001：401-404.

[7] KATO K，KURIMOTO M，SHUMIYA H，et al.Application of functionally graded material for solid insulator in gaseous insulation system[J].IEEE Transactions on Dielectrics and Electrical Insulation，2006，13（2）：362-372.

[8] 李文棟，刘哲，有晓宇，等.叠层式介电功能梯度绝缘子的介电常数分布优化[J].西安交通大学学报，2016，50（10）：19-26.

LI W D，LIU Z，YOU X Y，et al.Permittivity distribution optimization for multilayer dielectric FGM insulator[J].Journal of Xian Jiaotong University，2016，50（10）：19-26.（In Chinese）

[9] LIU Z，LI W D，WANG Y B，et al.Topology optimization and 3D printing fabrication feasibility of high voltage FGM insulator[C]// 2016 IEEE International Conference on High Voltage Engineering and Application （ICHVE）.Chengdu：IEEE，2016：1-4.

[10]QASIM S A，GUPTA N.Use of particle swarm optimization in the computation of an optimal permittivity distribution in functionally graded material insulators[C]//2015 International Conference on Condition Assessment Techniques in Electrical Systems （CATCON）. Bengaluru：IEEE，2015：184-188.

[11]李信，刘海昌，滕元成，等.功能梯度材料的研究现状及展望[J].材料导报，2012，26（19）： 370-372.

LI X，LIU H C，TENG Y C，et al.Research status and future directions on functionally graded materials[J].Materials Review，2012，26（19）： 370-373.（In Chinese）

[12]刘华炜，刘学武，张广文.功能梯度材料制备工艺及研究进展[J].机械设计与制造，2012（4）：265-267.

LIU H W，LIU X W，ZHANG G W.Research progress and preparing technology of functionally graded material[J].Machinery Design & Manufacture，2012（4）：265-267.（In Chinese）

[13]冯慈璋，马西奎.工程电磁场导论[M].北京： 高等教育出版社，2007： 21-22.

FENG C Z，MA X K.Introduction to engineering electromagnetic fields[M].Beijing：Higher Education Press，2007：21-22.（In Chinese）

[14]严璋，朱德恒.高电压绝缘技术[M].北京： 中国电力出版社，2007： 22-263.

YAN Z，ZHU D H.High voltage insulation technology[M].Beijing： China Power Press，2007：22-263.（In Chinese）

[15]马爱清，杨秀，陆鑫淼，等.GIS盘式绝缘子三维电计算及其逆问题分析[J].高电压技术，2010，36（5）：1217-1221.

MA A Q，YANG X，LU X M，et al.3D electric field calculation and its inverse problem analysis of disktype insulator in GIS[J].High Voltage Engineering，2010，36（5）：1217-1221.（In Chinese）

[16]徐大发.基于粒子群算法和有限元方法的薄壁圆筒夹持优化研究[D].重庆：重庆大学自动化学院，2016： 48-53.

XU D F.Study on the optimization of clamping of the thinwalled cylinder based on particle swarm optimization and finite element method[D].Chongqing：College of Automation， Chongqing University，2016：48-53.（In Chinese）

[17]黎斌.SF6高压电器设计[M].4版.北京：机械工业出版社，2015：82-94.

LI B.Design of SF6 high voltage electrical appliance[M].4th ed.Beijing： Mechanical Industry Press，2015：82-94.（In Chinese）