基于贝叶斯推理的乘员约束系统参数识别

卿宏军 谢宝娣 张连怡

摘 要：为了克服测量响应的不确定性给乘员约束系统参数识别带来的困难，利用马尔科夫链蒙特卡洛（Markov Chain Monte Carlo，MCMC）采样和近似模型构造技术，提出一种基于贝叶斯推理的乘员约束系统不确定性参数识别方法.该方法结合约束系统参数的先验分布和测量响应，通过马尔科夫链在未知参数联合概率密度空间进行抽样，从而获得了织带刚度缩放系数和质量流率缩放系数的后验边缘概率密度函数.识别结果表明，相比于传统确定性识别方法，基于贝叶斯推理的不确定性参数识别方法不仅能有效给出乘员约束系统参数的概率分布，而且能够保证参数寻优的全局收敛性.

关键词：贝叶斯方法；参数识别；约束系统；MCMC；代理模型

中图分类号：TH122 文献标志码：A

Abstract：In order to overcome the difficulty for the parameters identification of occupant restraint system caused by the measured uncertainty， this paper proposed an uncertain identification method for the parameters of occupant restraint system based on Bayesian inference， which combined Markov Chain Monte Carlo （MCMC） sample and surrogate model. This method firstly obtains the prior distributions of identified parameters and measured responses， and then the MCMC sampling is applied to the joint probability density of unknown parameter. Then， the marginal posterior probability distributions of scale factor of webbing and rate of flow can be calculated. Compared with the traditional method of determined identification， the identified results show that the Bayes inference method for uncertain parameter identification not only obtains the probability distributions effectively， but also ensures the global convergence of identified parameter.

Key words：Bayesian method；parameter identification； restraint system；MCMC；surrogate model

汽车乘员约束系统是在汽车发生碰撞事故时，为保护乘员及减轻乘员损伤的安全装置，主要由安全带、安全气囊、安全座椅、前后围板等组成.影响约束系统性能的参数众多，而某些参数难以通过直接测量的方式获得，因此利用测量响应对未知参数进行识别对于研究约束系统，提高车辆安全性是非常必要的[1-3].然而在实际中，由于试验条件的复杂性或测试设备精度的局限性等因素，测量响应往往具有一定的不确定性.传统的参数识别类方法，不管是基于梯度的最速下降法、高斯牛顿法等，还是智能优化算法的遗传算法、差分进化算法等，都忽略了不确定性的影响[4-7].但是当測量响应的不确定性对系统参数的识别具有重要影响而不可忽略时，采用传统确定性识别方法将难以提供可靠的结果.

不确定性的度量方式有很多种，概率度量是最为常用的一种方法，其采用概率密度函数（Probability Density Function，PDF）来描述不确定性[8].基于概率度量来进行不确定性参数识别已经取得了一些成果.该方法一般可分为两大类，贝叶斯推理[9]和基于优化的不确定性反求方法[10].Fonseca等[11]提出通过最大似然估计与摄动法或MCS相结合的方法处理不确定性参数识别，其中优化方法被采用来解决似然函数，但是该方法存在一个前提假设，即分布形式已知，因此难以处理分布形式未知的问题.为了解决分布未知的不确定性识别问题，刘杰等[12]提出了一种基于衍生的λPDF和一次二阶矩的不确定计算反求方法并将其应用在车辆行人碰撞事故的不确定性重建中.该方法用含有四参数的二次衍生λPDF对待识别参量的PDF进行建模，能够识别一大类单峰的PDF.贝叶斯推理作为另一种基于概率的不确定性分析方法，同样能够获得参数在整个定义域上的概率分布.Moore等[13]通过贝叶斯方法对裂纹参数进行了有效识别. Nasrellah等[14]将贝叶斯方法应用到动态系统的参数识别中.贝叶斯推理需要反复调用模型来获得参数的后验概率分布，所以计算效率较低.但是数值模拟技术和代理模型技术的发展[9，15，16]，使得基于贝叶斯推理的参数识别得到了广泛的应用，包括在工程结构、热传导等参数识别领域.

目前，基于贝叶斯推理方法在车辆系统参数识别中的应用还很少，为此本文以乘员约束系统模型为例，研究基于贝叶斯推理的不确定性参数识别方法，在对乘员约束系统的参数进行敏感性分析的基础上建立其代理模型，然后结合测量的不确定性响应和蒙特卡洛马尔科夫链采样方法，对织带刚度缩放系数和质量流率缩放系数的后验边缘概率密度函数进行估计，从而有效评价了不确定性因素对约束系统参数识别结果的影响.

1 约束系统不确定性识别问题描述

汽车乘员约束系统是在汽车发生碰撞时，用来减少或者避免二次碰撞的安全装置，是汽车安全设计的重要环节.采用MADYMO建立的某微车驾驶员侧约束系统模型如图1所示，该模型主要由安全带、安全座椅及安全气囊等组成.影响约束系统安全性能的参数众多，其中一些参数难以通过直接测量的方式获得，如座椅与假人的摩擦因数、安全带织物刚度缩放系数和气体质量流率缩放系数等，因此有必要利用测量响应对这类参数进行识别.

在实际工程中，由于试验条件的复杂性和测试设备精度的局限性等因素，测量WIC值往往具有一定的不确定性.传统的参数识别方法往往忽略了不确定性的影响，但是当测量响应的不确定性对系统参数的识别具有重要影响而不可忽略时，采用传统确定性识别方法将难以提供可靠的结果.因此，为了更加有效地评价WIC值的不确定性对待识别参数的影响，基于概率度量对约束系统模型参量识别问题可描述为已知损伤指标WIC的PDF，求约束系统不确定性参数的PDF，即

2 敏感性分析

在约束系统参数识别前，需对损伤指标WIC关于待识别参数之间的敏感性进行分析，筛选出对WIC值影响较大的参量.假设约束系统有了4个与安全带模型和气囊模型相关的未知参量，分别为座椅与假人的摩擦因数、安全带织物刚度缩放系数、气体质量流率缩放系数以及气囊透气率常数.首先采用正交试验设计方法来进行仿真试验，参量的3种不同水平表如表1所示.考虑如表2所示4种工况下的碰撞，分别为35 km/h正面碰撞和40 km/h的40%前端侧角碰撞，乘员模型分别为第50百分位男性假人和第5百分位女性假人.

求取表2中的4种工况下的WIC值，并利用方差分析鉴别各个模型参量对试验结果的影响.构造统计量F来检验，用P值来比较各个因素对结果影响的显著性，其中P值越小代表该因素对试验结果的影响越显著，分析结果如表3所示.

从表3可以看出，织带刚度缩放系数和流率缩放系数在所有工况下对WIC值都有显著影响，而座椅摩擦系数、透气率常数对所有工况的WIC值的影响都不显著，尤其是工况1和工况3.究其原因不难发现，安全带与安全气囊是保证人体最重要的部位即胸部与头部在发生意外时避免损伤最为关键的约束件，通常安全带与安全气囊的质量好坏对整个约束系统的保护效果具有直接的影响，而座椅为辅.同时，织带刚度缩放系数和气体质量流率缩放系数又是安全带与安全气囊质量的决定因素所在，这就造成了WIC值对安全带织物刚度缩放系数与气体质量流率缩放系数的变化比较敏感.由敏感性分析结果可知，表2中所示工况适于对织带刚度缩放系数和流率缩放系数进行识别，且在识别过程中可将座椅摩擦因数、透气率常数假设为一固定值.

3 基于贝叶斯推理的约束系统参数识别方法

基于贝叶斯方法的参数识别需要大量地调用仿真模型，为了提高计算效率，对选定待识别参量织带刚度缩放系数和流率缩放系数进行全因子试验设计

采样，利用试验中获取的样本点等信息，计算出涉及到全部试验因素的各水平响应值，最终建立系统的高近似度二阶响应面模型，如式（3）所示.式（3）中，X1为织带刚度缩放系数，X2为质量流率缩放系数，WIC1和WIC2分别为工况1和工况2下的损伤指标.

通过上述方法可获得织带刚度系数和流率缩放系数的分布形式，且后验概率分布中的概率最大值所对应的参数为参数识别中的最佳结果.对于式（4）一般采用数值积分方法进行求解，MCMC是一种常用的处理复杂问题的高维数值积分方法，而且其可以避免对式（4）中的正规化常数的求解.该方法主要是通过马尔科夫链利用抽样点之间的相关性产生有用样本点，只要样本足够多，那么统计样本得到的结果就越接近织带刚度系数和流率缩放系数的后验PDF.MetropolisHastings （MH） 算法[18]是常用的一种构造马尔科夫链的方法，该方法能够保证更多的样本点落在最重要的区域，以至于產生能够模拟真实未知参数联合后验PDF的足够多的样本点，从而提高计算效率.针对织带刚度系数和流率缩放系数，该方法生成各自马氏链{X0i，X1i，X2i，…}（i=1，2）的具体过程如下：

1）随机产生织带刚度系数和流率缩放系数的初始样本X0i；

2）构造待识别参数的建议分布p（X*iXi）；

3）当前样本Xji及提议分布p（X*iXi）产生待识别参数的候选样本X*i；

4）从0，1均匀分布随机产生u；

5）求解v=p（X*iWIC）p（X*iXji）p（XjiWIC）p（XjiX*i），若u≤v，则接受Xj+1i=X*i，进行步骤6）；否则Xj+1i=Xji并重复过程3） .

6）在马氏链达到平稳状态或满足链长条件时，输出识别的织带刚度系数和流率缩放系数的PDF.

4 识别结果与分析

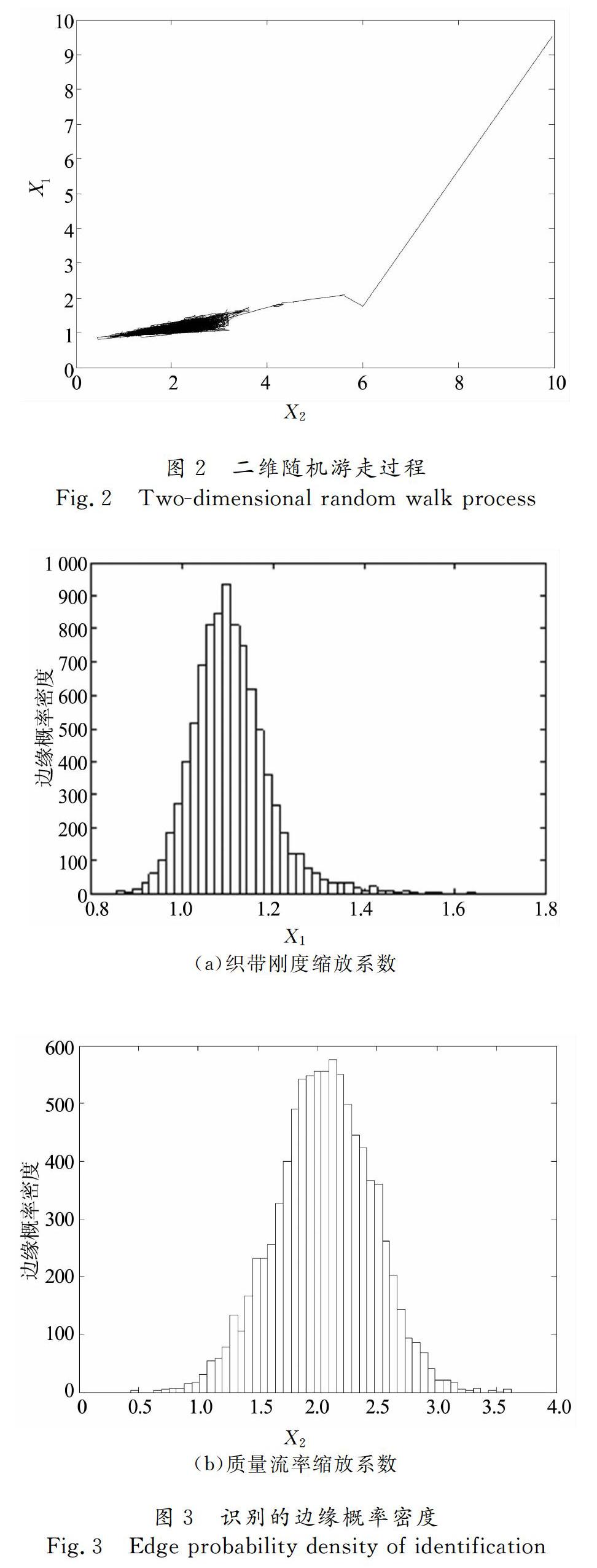
假定损伤指标WIC1值和WIC2值分别服从正态分布N1（0.52，0.01）和N2（0.40，0.01）， 迭代的初始点为[10，10].进行了10 000次迭代，识别的织带刚度缩放系数和质量流率缩放系数的二维随机游走过程如图2所示.从图2可以看出，只经过较少次数的迭代，该马尔科夫链就得到收敛.由识别结果可得织带刚度缩放系数和质量流率缩放系数的边缘概率密度如图3所示，均值和标准差如表4所示.

从图3和表4可以看出，织带刚度缩放系数和质量流率缩放系数的识别结果都为类正态分布，测量响应的不确定性对质量流率缩放系数的影响较大，而对织带刚度缩放系数的影响较小.通过获得的织带刚度缩放系数和质量流率缩放系数的边缘概率密度曲线有效地评价测量响应的不确定性对待识别参数结果的影响，相比于传统的确定性识别方法，本文方法识别的参数结果为一类正态分布而非一确定值，且结合参数敏感性分析可判断参数对WIC值的影响程度，这对汽车乘员约束系统的安全性设计具有更佳的指导意义.

5 结 论

为了有效评价测量响应的不确定性对汽车乘员约束系统中待识别参数的影响，本文发展了一種基于贝叶斯推理的乘员约束系统参数识别方法.该方法首先充分考虑了测量响应的不确定性，通过敏感性分析筛选出了约束系统中对WIC值影响较大的且难以通过直接测量得到的系统参数.其次基于近似模型构造技术对待识别参量进行全因子试验设计.利用试验中获得的涉及到全部试验因素的各水平响应值，建立系统的二阶响应面模型.最后利用基于贝叶斯推理的不确定性参数识别方法，有效地搜索乘员约束系统中待识别参数的后验分布，以此获得乘员约束系统参数最终识别结果.结果表明，相比于传统确定性识别方法，本文方法不仅能够保证参数寻优的全局收敛性，而且能有效地给出乘员约束系统中待识别参数的概率分布，可为汽车乘员约束系统的安全性设计提供更为全面的参考.

参考文献

[1] 钟志华，张维刚，曹立波，等.汽车碰撞安全技术[M]].北京：机械工业出版社，2003.

ZHONG Z H，ZHANG W G，CAO L B，et al.Automotive crash safety technology[M].Beijing：China Machine Press，2003.（In Chinese）

[2] 颜凌波，丁宗阳，曹立波，等.车车斜角碰撞工况下驾驶员损伤研究[J].湖南大学学报（自然科学版），2016，43（4）：59-66.

YAN L B，DING Z Y，CAO L B，et al.Study on the driver injury in vehicle to vehicle oblique crashes[J].Journal of Hunan University（Natural Sciences），2016，43（4）：59-66.（In Chinese）

[3] 李凡，曹迎春，粟思橙，等.后碰撞中乘员颈部肌肉有限元模型的建立与验证[J].湖南大学学报（自然科学版），2016，43（8）：45-51.

LI F，CAO Y C，SU S C，et al.Development and validation of a neck muscle FE model for rear impact study[J].Journal of Hunan University（Natural Sciences），2016，43（8）：45-51.（In Chinese）

[4] LIU J，XU C，HAN X，et al.Determination of the state parameters of explosive detonation products by computational inverse method[J].Inverse Problems in Science and Engineering，2016，24（1）：22-41.

[5] LIU J，HU Y F，XU C，et al.Probability assessments of identified parameters for stochastic structures using point estimation method[J].Reliability Engineering & System Safety，2016，156：51-58.

[6] 谢旭，李吉隆，赵俊亮，等.基于遗传算法的车辆参数识别方法[J].浙江大学学报（工学版），2010，44（9）：1818-1824.

XIE X，LI J L，ZHAO J L，et al.Identification method of vehicle parameters based on genetic algorithms[J].Journal of Zhejiang University（Engineering Science），2010，44（9）：1818-1824.（In Chinese）

[7] CHEN R，HAN X，LIU J，et al.A computational inverse technique to determine the dynamic constitutive model parameters of concrete[J].Computers Materials & Continua，2011，25（2）：135-157.

[8] BABUSKA I，SILVA R S.Dealing with uncertainties in engineering problems using only available data[J].Computer Methods in Applied Mechanics and Engineering，2014，270：57-75.

[9] CIVIDINI A，MAIER G，NAPPI A.Parameter estimation of a static geotechnical model using a Bayes approach[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts，1983，20（5）：215-226.

[10]LEDESMA A，GENS A，ALONOS E E.Estimation of parameters in geotechnical backanalysisI maximum likelihood approach[J].Computers and Geotechnics，1996，18（1）：1-27.

[11]FONSECA J R，FRISWELL M I，MOTTERSHEAD J E，et al.Uncertainty identification by the maximum likelihood method[J].Journal of Sound and Vibration，2005，288：587-599.

[12]刘杰，许灿，李凡，等.基于λPDF和一次二阶矩的不确定性计算反求方法[J].机械工程学报，2015，51（20）：135-143.

LIU J，XU C，LI F，et al.The uncertainty calculation inverse method based on λPDF and first order second moments[J].Journal of Mechanical Engineering， 2015，51（20）：135-143.（In Chinese）

[13]MOORE E Z，MURPHY K D，NICHOLES J M.Crack identification in a freely vibrating plate using Bayesian parameter estimation[J].Mechanical Systems and Signal Processing，2011，25：2125-2134.

[14]NASRELLAH H A，MANOHAR C S.Finite element method based Monte Carlo filters for structural system identification[J].Probabilistic Engineering Mechanics，2011，26：294-307.

[15]朱嵩，毛根海，程偉平，等.基于贝叶斯推理的水环境系统参数识别[J].江苏大学学报（自然科学版），2007，28（3）：237-240.

ZHU S，MAO G H，CHENG W P，et al.Parameters inentification for water environmental system based on Bayesian inference[J].Journal of Jiangsu University（Natural Science Edition），2007，28（3）：237-240.（In Chinese）

[16]李小华，谢礼立，公茂盛.结构物理参数识别的贝叶斯估计马尔可夫蒙特卡罗方法[J].振动与冲击，2010，29（4）：59-31.

LI X H，XIE L L，GONG M S.Structural physical parameter identification using Bayesian estimation with Markov Chain Monte Carlo method[J].Vibration and Shock，2010，29（4）：59-31.（In Chinese）

[17]VIANO D C，AREPALLY S.Assessing the safety performance of occupant restraint system[J]. Society of Automotive Engineers Transactions， 1990 ， 43 （43） ：1407-1413.

[18]HASTINGS W K.Monte Carlo sampling methods using Markov Chains and their applications[J].Biometrika，1970，57（1）：97-109.