敏度分层过滤策略克服连续体拓扑优化荷载病态问题

赵刚 刘杰 王洪鑫 杨兴发 文桂林

摘 要：针对工程结构中所承受载荷幅值之间相差多个数量级，使用传统拓扑优化方法所得结果中较小载荷传递路径消失的荷载病态现象，提出一种简单有效的敏度分层过滤策略.将各载荷以幅值大小进行分层，并计算各载荷对结构对应的应变能数值.在此基础上，引入比较判断系数和放大应变能影响系数，将各灵敏度以大小进行分层，对不同层次灵敏度进行不同的过滤以取得多载荷作用下最佳材料布局.本文敏度分层过滤策略是在Solid Isotropic Material with Penahiation（SIMP）框架下提出的，并使用Optimality Criteria（OC）方法进行求解.使用二维和三维算例验证了所提策略的有效性，表明该策略可以有效克服荷载病态现象，为结构设计中得到完整传力结构布局提供重要指导.

关键词：结构优化；荷载病态；SIMP方法；敏度分层过滤；拓扑优化

中图分类号：TH122；TU318.1 文献标志码：A

Abstract：To solve the phenomenon of load sickness in which the transfer path of the weak load disappears by using the traditional topology optimization method， a simple and effective strategy of sensitivity hierarchical filtering was proposed. The loads were stratified by magnitude， and the strain energy corresponding to the structure was calculated. On this basis， two coefficients were introduced， which were used for comparison and amplifying the influence of strain energy. Then， the sensitivities were stratified on the basis of degree， and the sensitivity of different stratification was filtered by different filters to obtain the optimal material layout under multiload. The strategy was proposed in the framework of SIMP and solved by OC method. Both twodimensional and threedimensional numerical examples were presented to show the effectiveness of the proposed strategy， demonstrating that the strategy can effectively overcome the phenomenon of load sickness， and provide important guidance for the completed structural force distribution of the structure.

Key words：structure optimization；load sickness；SIMP method；hierarchical sensitivity filtering；topology optimization

結构拓扑优化是指在给定的载荷和约束条件下，通过改变结构材料布局使结构的目标性能达到最优[1-4].与尺寸优化和形状优化相比[5-7]，结构拓扑优化能够在初始设计阶段得到全新的构型设计，获得更大的经济效果，是近年来的研究热点.连续体拓扑优化应用范围广，模型构造困难，设计变量多，计算量大，因此很长一段时间里发展十分缓慢.Bendsoe等人[8]首次提出一种连续体拓扑优化方法——均匀化方法.随后，连续体拓扑优化得到了迅速发展，出现了SIMP法[9-11]、渐进结构优化方法[12-15]、水平集法[16-18]等.其中，SIMP法是在均匀化方法基础上提出的，目前应用最广泛.

在实际工程中，当结构所受最大载荷与最小载荷相差悬殊时，优化得到的拓扑结构常常会出现小载荷的传递路径模糊不清甚至完全消失的现象，从而导致优化结构与工程实际不符.这一现象与结构分析时刚度相差悬殊导致的“总刚病态”类似，称之为“荷载病态”[19-22].该问题目前研究较少.如果用减小阈值（单元设计变量小于阈值的单元被删除，大于阈值的单元被保留）来保留传递小载荷的单元，则大载荷的弱区域也会受到影响，就会对最终整体结构的优化形状造成很大的改变，从而导致得不到最优拓扑结构.王健等[19]采用分层优化技术解决该问题，其基本思想是按载荷大小分为几个层次，并从大到小分别进行优化.第1层优化时得到传递第1层载荷的结构，第2层优化时，去除第1层载荷，保留第1层优化得到的结构单元不变，并参与第2层结构优化计算，但这些单元不作为设计变量，对其余单元进行优化计算，得到传递第2层载荷的结构，依次类推，去除属于前面的载荷，保留之前的优化得到的结构单元，用剩余单元优化出传递较小载荷的结构，直至结束.由于这种分层优化方法只考虑每一层内载荷相互作用的结果，因而不能综合考虑全部载荷的共同作用效果，最终得到的优化结构与原始优化结构有较大区别，并且也不便于对整体结构的体积等条件进行约束.隋允康等[20-22]采用ICM应力全局化方法解决该问题，其基本思想是以结构应变能作为权系数处理载荷，通过加权减小载荷间的差距，按修正的载荷计算最优拓扑.由于这种方法本质上是对小载荷进行放大计算，最终得到的优化结构与原始的优化结构相差较大，对主要载荷的传递路径有一定影响.Hu等人[23]建议采用应变能修改对应的载荷下体积分配来处理ESO法中的荷载病态问题.Cai等人[24-25]提出分数模常法，通过改变各载荷对应的应变能函数克服该问题.这两种方法都是在分层优化法和加权系数法的基础上进行的改进.

本文在分析减小阈值法、分层优化法、加权系数法等处理荷载病态的弊病后，提出了一种用应变能处理、敏度分层过滤解决“荷载病态”的策略.这种策略的好处在于能够清晰显示小载荷的传递路径，同时适用于二维平面结构和三维空间结构，并且对多载荷共同作用得到的原始优化结构改变较小，克服了大多数方法为显示小载荷路径而改变整体结构的劣势.

1 多载荷下的结构拓扑优化模型

1.1 基于SIMP密度插值方式的拓扑优化模型

2 利用敏度分层过滤克服荷载病态

2.1 荷载病态现象

实际工程中，结构通常在复杂的受力情况下工作，不同载荷对结构的要求有差别.在连续体结构拓优化中，当结构所受最大载荷与最小载荷相差多个数量级时，优化所得结果中会出现小载荷传递路径模糊不清甚至完全消失的现象，导致优化结构与工程实际不符.这一现象称之为“荷载病态”.如图1所示，图1（a）为基结构，P1为大载荷，P2为小载荷，载荷大小比例P2 /P1=1/1 000.在这种情况下，最优拓扑结构如图1（b）所示，小载荷的传递路径虽然被保留了，但是显示模糊，导致无法制造.该现象出现的原因在于小载荷与大载荷对结构的作用效果相差较大，因此小载荷传递路径的单元拓扑值很小，在进行敏度过滤时，小载荷传递路径周围的单元应变能影响很小，因而得到的更新拓扑值也很小，结构不能清晰显示.小载荷传递路径消失是由于在优化算法中设定了阈值，当单元拓扑值小于阈值时则删除该单元.如果用减小阈值法来保留传递小载荷的单元，则大载荷的弱区域也会被保留，从而导致最终整体结构的优化形状不够清晰，不能得到最优拓扑结构.

2.2 敏度分层过滤策略

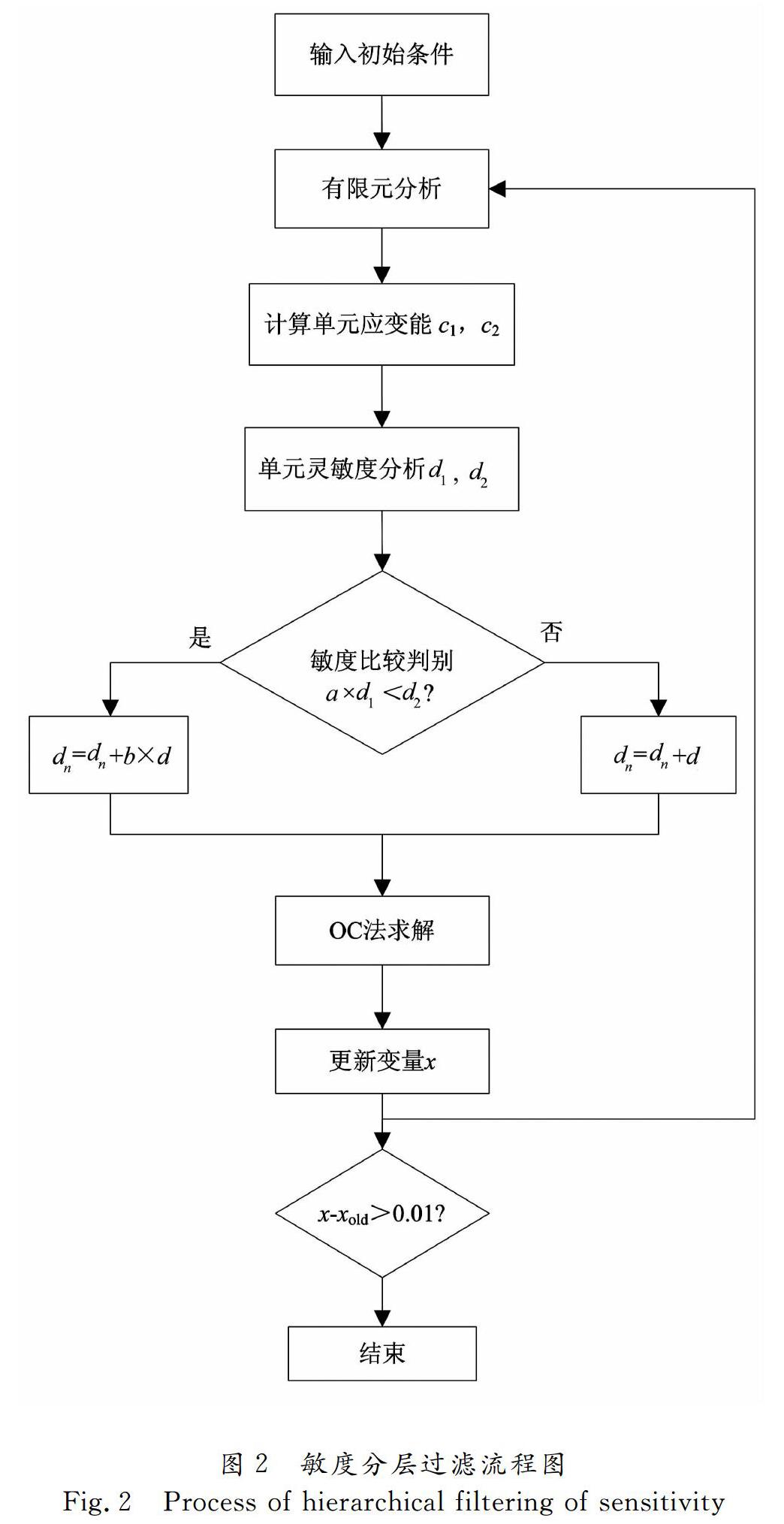
针对荷载病态问题，敏度分层过滤策略是一种很有效的策略.敏度分层过滤策略的基本思想是：按幅值大小将载荷分为几个层次，在每一次的迭代中，分别计算出各载荷对结构各个单元对应的应变能数值，并进行灵敏度分析，通过比较判断系数将各灵敏度以大小分层，对不同层次的灵敏度采用不同的敏度过滤，最终得到优化结构是多个载荷综合作用的结果.下面以单工况两个载荷为例来介绍该策略实现过程：

1） 建立有限元模型，设置载荷及边界条件；

2） 采用有限元方法分析结构响应；

3） 提取各载荷对每个单元的应变能c1、c2，其中c1是小载荷F1作用的应变能，c2是大载荷F2作用的应变能；

4） 对两个载荷作用的应变能分别进行灵敏度分析得到d1、d2，其中d1是F1对应的灵敏度，d2是F2对应的灵敏度.d是两个载荷共同作用的灵敏度分析结果，dn是全局敏度矩阵.

5） 通过判别条件将d1与d2进行比较，将灵敏度以数值大小分层，并选择不同的过滤算法进行过滤；

6） 使用OC算法求解；

7） 更新设计变量x；

8） 检查是否满足优化终止条件.若满足，则优化结束，若未达到终止条件，则返回至步骤2）.

敏度分层过滤流程图如图2所示.

在敏度分层过滤流程中，通过判别条件，将d1和d2进行比较，以数值大小将灵敏度分层，并选择不同的过滤算法进行过滤.由于即使是在小载荷作用点处，大载荷的影响也可能比小载荷大，因此需要乘以一个系数a进行比较.当该判别条件不成立时，不改变过滤方式；当判别条件成立时，通过乘以加权系数b放大周围单元应变能的影响，使得OC算法得到的拓扑值x放大.

通过分析与比较多种结果可以发现，系数a主要对载荷传递路径有一些改变，系数a较大时，小载荷对路径的影响较为明显.系数b主要对拓扑值x的大小有影响，系数b较大时，最终显示的结构颜色黑白比较明显.

3 数值算例

3.1 算例1

初始结构为一300 mm×200 mm的长方形平面区域，左右两边受固定支撑，单工况内受两个载荷作用，载荷F1=1 000 N，作用于上边界中点，方向向下，载荷F2=1 N，作用于下边界中点，方向向上，如图3所示，优化体积系数f = 0.5.划分60×40个矩形网格单元，使用敏度分层过滤策略前SIMP法优化结果如图4所示.采用不同的系数a、b进行敏度分层过滤优化结果如图5所示.

比较图5（a）和图5（b）可知，系数b越大，优化结构图像越清晰，系数b主要影响拓扑值x的大小；比较图5（a）和图5（d）可知，系数a增大，小载荷传递路径的影响增大，系数a主要改变小载荷传递路径的影响.

图4与图5中各结构最小应变能与计算迭代步数如表1所示，其中最小应变能未对灰度单元作调整.比较可知，使用敏度分层过滤策略对整体结构的影响较小，结构最小应变能随着系数a增大而减小，随着系数b增大而增大，并且系数a和b也能够减少迭代步数.

结合图5和表1结果可知，在平面问题中，敏度分层过滤策略在改善图形显示的同时保留了原始优化结构，有效地处理了荷载病态问题，是合理可行的.

3.2 算例2

基本结构为一180 mm×120 mm的长方形平面区域，左边受固定支撑，两个载荷同时作用，载荷F1=1 000 N，作用于右下角，方向向下，载荷F2=1 N，作用于右上角，方向向上，如图6所示，优化体积系数f =0.3，划分60×40个矩形网格单元.使用SIMP法优化结果如图7（a）所示，使用敏度分层过滤策略优化结果如图7（b）所示.

由图7可以发现，使用SIMP法优化该结構时，由于F1远大于F2，导致F2的传递路径几乎消失.敏度分层过滤策略通过放大小载荷F2周围单元应变能的影响，将F2的传递路径有效地显示.因此，使用敏度分层过滤策略在处理悬臂梁荷载病态问题时是有效可行的.

3.3 算例3

初始结构为一600 mm×400 mm×40 mm的长方体三维区域，左右两端面受固定支撑，受两个载荷作用，载荷F1=1 000 N，作用于基结构顶面中心，方向向下，载荷F2=1 N，作用于基结构底面中心，方向向上，划分60×40×4个长方体单元，如图8所示，优化体积系数f = 0.5.使用SIMP法的优化结果如图9（a）所示，使用敏度分层过滤策略后的拓扑优化结果如图9（b）所示.

由圖9（a）可以看出，SIMP法在处理三维荷载病态问题时，小载荷的传递路径完全被删除，所得优化结构不符合工程实际情况.

结合图9（b）和图4可以发现，在三维问题中，敏度分层过滤策略在处理荷载病态问题时能够发挥很好的作用，小载荷的传递路径被保留并清晰显示，因此该策略在三维结构优化中也是有效可行的.

3.4 算例4

基本结构为一120 mm×80 mm×8 mm的长方体三维悬臂梁，两个载荷同时作用，载荷F1=1 000 N，作用于基结构右下角棱边中点，方向向下，载荷F2=1 N，作用于基结构右上角棱边中心处，方向向上，划分60×40×4个长方体单元，如图10所示，体积系数f = 0.4.SIMP法拓扑优化结果如图11（b）所示，敏度分层过滤策略处理结果如图11（c）所示，加权系数法处理结果如图11（d）所示.

载荷F1单独作用、SIMP法、加权系数法和敏度分层过滤策略得到的最优结构最小应变能如表2所示，其中灰度单元应变能未调整.

由图11和表2可知，在SIMP法中，只考虑了大载荷对结构的影响，小载荷的作用被完全忽略；加权系数法较大地改变了原始构型，对结构的最小应变能影响较大；而使用敏度分层过滤策略不仅可以清晰完整地显示出小载荷的传递路径，且对结构的最小应变能改变较小.结合算例2的优化结果可以发现，由于敏度分层过滤策略在三维结构中考虑的是球形区域内单元应变能的影响，而在二维中考虑的是圆形区域内单元应变能的影响，因此使用敏度分层过滤策略处理三维荷载病态问题的效果比二维更理想.

4 结 论

基于工程结构拓扑优化中的荷载病态问题，通过在传统的SIMP方法中引入两个关键系数，提出了一种敏度分层过滤策略.数值算例结果表明：

1）敏度分层过滤策略能够得到较为清晰的结构，显示出小载荷的传递路径，可有效地克服荷载病态问题；

2） 使用敏度分层过滤策略得到的优化结构与SIMP法优化结构较为接近，结构最小应变能改变较小；

3） 敏度分层过滤策略能够同时适用于二维平面结构与三维空间结构，可以为工程中结构荷载病态问题提供重要的指导作用.

参考文献

[1] 罗震，陈立平，黄玉盈，等.连续体结构的拓扑优化设计[J].力学进展，2004，34（4）：463-476.

LUO Z，CHEN L P，HUANG Y Y，et al.Topological optimization design for continuum structures[J].Advances in Mechanics，2004，34（4）：463-476.（In Chinese）

[2] 夏天翔，姚卫星.连续体结构拓扑优化方法评述[J].航空工程进展，2011，2（1）：1-11.

XIA T X，YAO W X.A survey of topology optimization of continuum structure[J].Advances in Aeronautical Science and Engineering，2011，2（1）：1-11.（In Chinese）

[3] DEATON J D，GRANDHI R V.A survey of structural and multidisciplinary continuum topology optimization：Post 2000[J].Structural and Multidisciplinary Optimization，2014，49（1）：1-38.

[4] 唐东峰，游世辉.基于可靠性的结构动态拓扑优化方法[J].湖南大学学报（自然科学版），2017，44（10）：62-67.

TANG D F，YOU S H.Reliabilitybased structural dynamic topology optimization method[J].Journal of Hunan University （Natural Sciences），2017，44（10）：62-67.（In Chinese）

[5] 周克民，李俊峰，李霞.结构拓扑优化研究方法综述[J].力学进展，2005，35（1）：69-76.

ZHOU K M，LI J F，LI X.A review on topology optimization of structures[J].Advances in Mechanics，2005，35（1）：69-76.（In Chinese）

[6] DEDE T，AYVAZ Y.Combined size and shape optimization of structures with a new metaheuristic algorithm[J].Applied Soft Computing，2015，28（S）：250-258.

[7] LI C，KIM I Y，JESWIET J.Conceptual and detailed design of an automotive engine cradle by using topology，shape，and size optimization[J].Structural & Multidisciplinary Optimization，2015，51（2）：1-18.

[8] BENDSOE M P，KIKUCHI N.Generating optimal topologies in structural design using a homogenization method[J].Computer Methods，1988，711：197-224.

[9] SIGMUND O.A 99 line topology optimization code written in MATLAB[J].Structural & Multidisciplinary Optimization，2001，21（2）：120-127.

[10]BENDSE M P，SIGMUND O.Material interpolation schemes in topology optimization[J].Archive of Applied Mechanics，1999，69（9/10）：635-654.

[11]ZEGARD T，PAULINO G H.Bridging topology optimization and additive manufacturing[J].Structural & Multidisciplinary Optimization，2016，53（1）：175-192.

[12]XIE Y M，STEVEN G P.A simple evolutionary procedure for structural optimization[J].Computers & Structures，1993，49（5）：885-896.

[13]GHABRAIE K.The ESO method revisited[J].Structural & Multidisciplinary Optimization，2015，51（6）：1211-1222.

[14]LIU J，WEN G，XIE Y M.Layout optimization of continuum structures considering the probabilistic and fuzzy directional uncertainty of applied loads based on the cloud model[J].Structural and Multidisciplinary Optimization，2016，53（1）：81-100.

[15]LIU J，WEN G，QING Q，et al.An efficient method for topology optimization of continuum structures in the presence of uncertainty in loading direction[J].International Journal of Computational Methods，2016：1750054.

[16]WANG M Y，WANG X，GUO D.A level set method for structural topology optimization[J].Computer Methods in Applied Mechanics and Engineering，2003，192（1）：227-246.

[17]荣见华.一种改进的结构拓扑优化水平集方法[J].力学学报，2007，39（2）：253-260.

RONG J H.An improved level set methed for structural topology optimization[J].Chinese Journal of Theoretical and Applied Mechanics，2007，39（2）：253-260.（In Chinese）

[18]COFFIN P，MAUTE K.A levelset method for steadystate and transient natural convection problems[J].Structural & Multidisciplinary Optimization，2016，53（5）：1047-1067.

[19]王健，程耿东.多工况应力约束下连续体结构拓扑优化设计[J].机械强度，2003，5（1）：55―57.

WANG J，CHENG G D.Topology optimization design of the continuum structure for multiple loading conditions with stress constraints[J].Journal of Mechanical Strength，2003，5（1）：55-57.（In Chinese）

[20]隋允康，楊德庆，王备.多工况应力和位移约束下连续体结构拓扑优化[J].力学学报，2000，32（2）：171―179.

SUI Y K，YANG D Q，WANG B.Topological optimization of continuum structure with stress and displacement constraints under multiple loading cases [J].Chinese Journal of Theoretical and Applied Mechanics， 2000，32（2）：171-179.（In Chinese）

[21]杨德庆，隋允康.多工况应力约束下连续体结构拓扑优化映射变换解法[J].上海交通大学学报，2000，34（8）：1061-1065.

YANG D Q，SUI Y K.Mapping transformation method for topology optimization of continuum structures under multiple loading cases and stress constraints[J].Journal of Shanghai Jiaotong University，2000，34（8）：1061-1065.（In Chinese）

[22]隋允康，彭細荣，叶红玲.ICM应力全局化方法克服连续体拓扑优化的荷载病态[J].工程力学，2009，26（6）：1-9.

SUI Y K，PENG X R，YE H L.Load sickness treatment in topology optimization of continuum structure by ICM method with stress globalization[J].Engineering Mechanics，2009，26（6）：1-9.（In Chinese）

[23]HU X G，CHENG H M，TAO Y.Modified rejection ratio for multiple load cases evolutionary structural optimization[J].Procedia Engineering，2012，31（1）：627-633.

[24]CAI K，SHI J，ZHANG A.Stiffness design of a continuum under illload cases by fractionalnorm objective formulation[J].Optimization & Engineering，2014，15（4）：927-944.

[25]CAI K，CAO J，SHI J，et al.Layout optimization of illloaded multiphase bimodulus materials[J].International Journal of Applied Mechanics，2016，8（3）：1650038.

[26]左孔天，陈立平，钟毅芳，等.基于人工材料密度的新型拓扑优化理论和算法研究[J].机械工程学报，2004，40（12）：31-39.

ZUO K T，CHEN L P，ZHONG Y F，et al.New theory and algorithm research about topology optimization based on artificial material density[J].Chinese Journal of Mechanical of Mechanical Engineering，2004，40（12）：31-39.（In Chinese）

[27]ANDREASSEN E，CLAUSEN A，SCHEVENELS M，et al.Efficient topology optimization in MATLAB using 88 lines of code[J]. Structural & Multidisciplinary Optimization，2011，43（1）：1-16.

[28]LIU K，TOVAR A. An efficient 3D topology optimization code written in MATLAB[J].Structural & Multidisciplinary Optimization，2014，50（6）：1175-1196.

[29]WANG H，LIU J，QIAN X，et al.Continuum structural layout in consideration of the balance of the safety and the properties of structures[J].Latin American Journal of Solids & Structures，2017，4（6）：1146-1172.