基于模拟退火粒子群算法的电网故障行波定位装置布点优化

杨洪灿，李寅，孙建

（云南电网有限责任公司曲靖供电局，云南曲靖655000）

配电网作为电力传输的最后一环，与用户有着紧密的联系[1]，其安全、可靠性直接影响着用户的用电体验[2-4]。当配电线路发生故障时，将中断用户的供电，直接影响用户的生产和生活[5]。因此，及时定位、解决电网故障对保证可靠的供电环境、改善用户用电体验、提高电网公司的服务质量具有重要意义[6-8]。

根据配电网故障定位采集的信号和选线方式的不同，可将故障定位方法分为基于稳态量[9]、基于故障暂态量[10]和基于特殊信号的方法[11]。由于配电网具有复杂的线路结构和较小的线路电容，在实际运行时电流极度不平衡。因此，较难检测和判别故障电流[12]。针对这一问题，众多专家和学者提出了基于暂态行波的故障定位方法，并取得了较好的应用效果[13]。该种方法针对配电网分支多、结构复杂的特点，使用大量的全球定位系统、高速数据采集设备、传感器和故障检测器来捕捉配电网的瞬态波形，从而定位故障。但这一方法需要安装、使用大量的检测装置造成冗余和浪费[14]。

1 配电网行波检测装置布点问题

行波检测装置一般分布在变电站内，然而配电网由众多长度较短的线路分支组成，若在每一个分支线路上均安装行波检测装置将需要耗费巨大的人力和物力。因此，需要区别对待配电网与行波检测装置的布点分布，使用更合理的布点方式。

由文献[15]可知，基于多测点的行波检测方法能更快、更准确地定位配电网故障。同时，当行波检测装置位于变压器二次侧时，可以获取到更明显的故障信号。因此，本文将行波检测装置布置在变压器二次侧。

1.1 优化目标定义

行波检测布点优化的目的是保证当配电网中某一条线路发生故障时，至少有一处行波检测装置能检测到故障信号，或者能结合多组检测装置的数据定位到故障位置。因此，本文将行波检测装置的最优配置问题定义为：使用最少的行波检测装置来观测配电网中的所有线路，对于一个由M条边和N个顶点组成的配电网，其行波检测装置布点优化问题可表示成如式（1）所示的0-1优化模型。

式中，S(f)表示配电中布置的行波检测装置的总数；fi表示配电网顶点是否布置行波检测装置，1表示布置，0表示不布置；Lj表示能否观测到配电网线路j的故障，1表示能观测，0表示不可观测。

1.2 约束条件定义

本文使用无向图G=（V，E）表示配电网各线路间的拓扑关系。其中，V为图的节点表示配电网的母线、电源或中断节点，E为图的边表示配电网的支路。可以使用如式（2）所示的邻接矩阵描述图G：

式中，n为无向图节点的数量，a表示两节点i与j是否直接相连。

图1 含分布式电源的配电网结构示意

表1 起点A的最短路径搜索结果

图2 配电网分层结构

使用配电网的无向图表示方法，可以对配电网进行分层，从而确定行波检测装置布点优化的约束条件。对于图1所示的含分布式电源配电网结构，以A为源节点，搜索其到电网其他节点的最短路径，得到如表1所示的结果。统计表1所示的各最短路径所经过的顶点，将经过点最多的路径作为配电网的第一层。依次以第一层的顶点作为第二层的起始点，搜索最短路径，重复使用上述步骤可得到如图2所示的配电网分层表示。

根据行波检测布点优化的目的可知，若能保证配电网的每一层均能被观测到。则当配电网任意一条线路发生故障时，均可及时定位。下面依次分析各子线路发生故障时，行波检测装置的布点优化条件。

1）主线路故障：当配电网主线路发生故障时，若在故障点的两侧布置检测装置即可观测整条线路。则有：

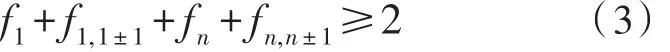
式中f1和fn分别表示主线路的首尾端点，f1,1±1和fn,n±1分别表示由于首端点和尾端点间节点数为1的节点。

2）简单分支故障：简单分支即图1所示的aB分支和bC分支。由于简单分支上不再含有其他分支线路，故使用b节点量测安装的行波检测装置即可观测到bC分支的故障。所以，对于简单分支可以不布置检测装置。

3）复杂分支发生故障：复杂分支即图1所示的cF分支线路，当其发生故障时可根据线路的冗余情况选择具体的行波检测装置的安装位置。有如下式（4）所示的约束条件：

式中，fni表示第i条分支线路的末端节点。

2 模拟退火粒子群算法

模拟退火算法是由N.metropolis等人根据固体降温过程与优化问题之间的相似性，提出的求解最优化问题的方法，其被广泛应用于管理科学和工程科学的组合优化问题中。模拟退火算法首先确定初始温度值，并得到一个随机初始解；然后以较大的概率接收较好的解，以较小的概率接收较差的解，直至系统冷却。其能在温度下降足够慢和初始温度足够高的情况下收敛到全局最优解。

粒子群算法是由Eberhart和Kennedy从现实生物群体活动开发出的智能优化算法，具有简单、收敛速度快和参数易设置的特点。然而，粒子群算法容易产生随机振荡，并易陷入局部最优解。因此，文献[16]使用模拟退火算法解决粒子群优化算法的缺点，提出了一种模拟退火粒子群算法。该算法将模拟退火机制引入到粒子群优化算法的粒子位置和速度更新机制中，按照较大的概率接受粒子群优化后的值，并按较小的概率接受恶化解。从而根据粒子能量的衰减搜索全局最优解。该算法不仅能避免陷入局部最优解，且还可以大幅提高粒子群优化算法的计算速度、提升算法性能。具体的算法步骤如下：

1）初始化：模拟退火算法的起始温度：T和T0，退火速度K；粒子群优化算法的惯性常数和加速度常数C1、C2；

2）根据预先设定的优化目标计算适应度值f(Xi(t))(i=1,2,3,…n)；

3）分别将每个粒子的适应度值f(Xi(t))与其极值进行比较，取出较优的粒子后更新极值；

4）分别将每个粒子的适应度值f(Xi(t))与全局极值进行比较，取出较优的粒子后更新全局极值；

5）更新粒子位置和速度，并归一化粒子速度；

6）计算粒子更新后的适应度值f(Xi(t+1))；

7）计算适应度的变化量 ΔE，若 ΔE＜0或EXP(-ΔE/T)＞ε则接收新的粒子位置；否则，拒绝。当粒子接收新的位置时，降温T并返回步骤（2）。

3 电网故障行波定位装置布点优化求解

文中使用上文介绍的模拟退火粒子群算法，求解最优的行波检测装置的布点分布。优化目标为式（1）所示的函数，约束条件为式（3）和式（4），具体的求解过程为：

1）将给定的配电网抽象为式（2）所示的拓扑图结构，用图的边表示线路，图的顶点表示行波检测装置的位置及分布式电源的接入点；

2）使用1.2所述的方法对拓扑图进行分层，并建立式（3）和式（4）所示的约束条件；

3）初始化模拟退火粒子群算法的参数；

4）使用式（1）计算各粒子的适应度值，并根据全局极值和适应度值更新各粒子的速度与位置；

5）对比式（3）和式（4）的约束条件，若粒子位置不满足约束条件，则惩罚当前粒子位置；否则，计算目标函数值并更新全局极值和最优粒子个体；

6）若达到迭代停止条件，则退出；否则，跳到步骤5）。

该算法步骤所对应的优化流程，如图3所示。

4 算例分析

文中首先使用算例验证了模拟退火粒子群优化算法的有效性，然后仿真测试了该算例的实际运行效果。测试使用的配电网拓扑结构，如图4所示。其分层结果，如图5所示。

该配电网的优化目标与式（1）相同，根据图5所示的分层结构，可得到该配电网的约束条件为：

图3 优化算法流程图

图4 测试配电网拓扑结构

图5 测试配电网分层结构图

设置模拟退火粒子群算法的初始解为1111111111111111，使用上文的算法可得到最终结果为1000100001001001，即将行波检测装置安装在AEJMP点处。

使用PSCAD软件搭建图4所示的配电网，测试模拟退火粒子群算法得到的优化结果。设置采样频率为10 kV，各线路长度如表2所示。

根据行波故障检测的原理可知，故障点两端的检测装置均能检测到故障信号，且两端检测到的信号存在时间差。根据计算得到的时间差可求得故障点的具体位置。其故障点位置可由式（6）计算得到：

表2 仿真测试系统中各线路长度

式中，LMF表示端点M到故障位置的距离，v为行波在电网中的传输速度，tM为行波到达端点M的时间，tN为行波到达端点N的时间，l为MN两点与故障点的最短传输路径长度。如图6和图7所示为P点观测到的电压信号和电压极大模值，根据这两种信号可准确的定位配电网中故障的具体位置。

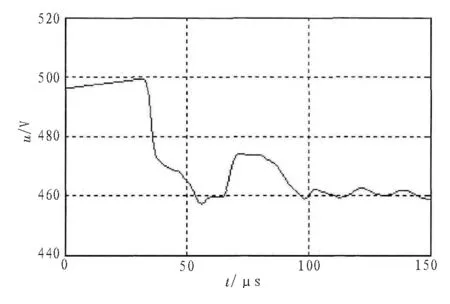
图6 P点观测到的电压信号

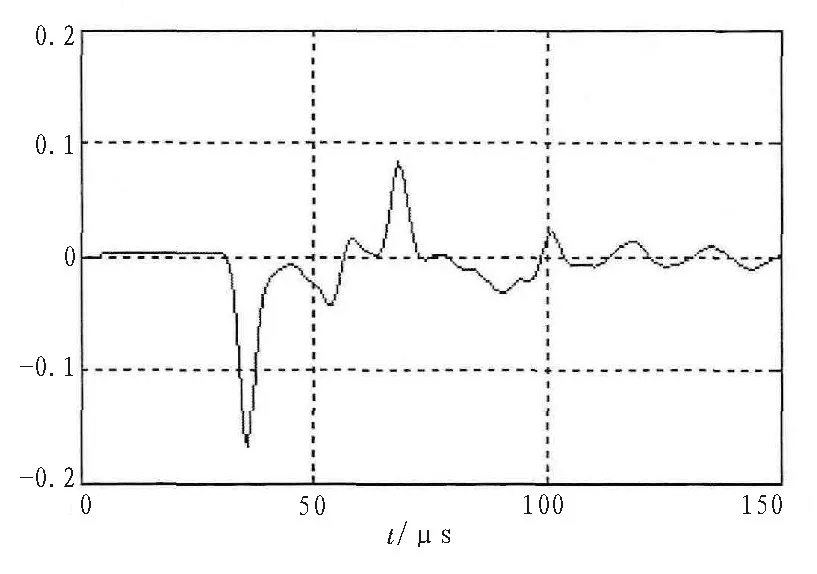
图7 P点观测的电压模极大值

5 结束语

为了节省配电网故障定位的装置数量和投资成本，文中提出一种基于模拟退火粒子群算法的电网故障行波定位装置布点优化算法。首先，为了保证当配电网中某一条线路发生故障时，至少有一处行波检测装置能检测到故障信号，或者能结合多组检测装置的数据定位到故障位置，从而定义了行波检测装置布点的优化目标；然后，根据配电网所对应的拓扑图及其分层模型定义了优化的约束条件；最后，使用模拟退火粒子群优化算法求解优化问题，得到最优分布。算例测试结果表明，所提出的方法能准确、高效地检测出配电网各分支线路的故障位置。