一种改进的无控制DEM匹配算法

刘志卫,朱建军,左廷英,周 璀

(1.中南大学 地球科学与信息物理学院，湖南 长沙 410083;2.中南林业科技大学 理学院，湖南 长沙 410018)

随着DEM获取方式的发展，DEM的空间分辨率和时间分辨率越来越高，由于DEM获取手段和获取时间的不同，使得同一区域的不同时相DEM覆盖区域不可能完全重合。传统的方法要求找到两组数据之间的多对同名点，通过坐标转换寻求两组数据之间的转换参数，才能使两组数据匹配到同一坐标系下。但是在高山区和分辨率较低的地图上，很难获取准确的地面控制点或同名特征点，因此，基于无控制点的DEM匹配具有广泛的引用价值。此外，DEM无控制匹配不仅可以确定两组数据之间的绝对定向参数[3]，将其匹配到同一坐标系下，也能根据不同时相的数据探测到地表一定程度的变形量[4-5]。

DEM无控制匹配最早是由Ebner和Mueller[6-7]提出的，其主要目的是用于立体模型的绝对定向。针对无控制DEM匹配问题，Rosenholm和Torlegard[8]提出的最小高程差(LZD,Least Square Z-axes Differences)算法，是为了寻找一种代替传统的使用控制点进行绝对定向的方法，且获得了比传统的使用控制点方法更高的匹配精度；Zhang等人[5]基于LZD算法结合差分模型，通过对不同点进行自适应加权，实现了DEM表面变形量的自动探测；Karras[9]在LZD算法的基础上，引入数据探测技术得到了稳健的LZD算法，能够探测到一定程度的变形。但是，利用LZD算法进行匹配时，很难选取合适的初始转换参数(包括尺度系数、平移参数和旋转参数)，这会对算法的收敛速度和计算效率产生很大的影响。

最近邻点迭代(ICP)算法是由Besl等[10]提出来的，该算法通过两个点集任意对应点间的距离平方和最小为原则来求解转换参数(3个旋转参数和3个平移参数)，使得两个表面的姿态更加接近。但是，传统ICP算法的缺点是，只适用于存在明确对应关系的点集之间的定位。此外，该算法也需要消耗大量的计算时间[11-12]，为此许多学者都提出了改进方法。方邵江等人[13]提出了使用加权最小二乘进行配准；袁建英等人[14]提出改进的ICP算法，实现重合区域的快速自动定位，实现不同视下点云的快速精确配准。

依上述可以得出，ICP算法采用搜索距离最小的点作为对应点对，其计算距离比较复杂，这使得算法迭代收敛速度很快，几次迭代计算就可以很好地接近真值，但是整体计算效率很低；而LZD算法由于建立对应关系的准则较简单，计算量小，整体计算效率较高，但是对于姿态差异较大的模型迭代次数较多，收敛速度较慢。因此，本文在ICP算法的基础上，提出一种融合ICP与LZD的改进无控制DEM匹配算法，并在传统最小二乘估计的基础上引入差分模型求抗差解，最后通过模拟实验和实测数据对改进算法进行验证，实验结果表明，改进后的算法在配准准确的基础上，不仅克服了传统ICP算法的局限性，也解决了LZD匹配算法由于初值选择问题所导致的收敛效率低的问题，提高了无控制DEM匹配的收敛速度和配准精度。

1 ICP和LZD匹配算法的基本原理

ICP(迭代最近点法)算法主要用于三维点云数据的配准问题，其主要思想是通过一定的方法获取两点云数据集间点与点之间的对应关系，并使所有对应点之间的距离最近，重复这个过程直到待匹配模型上所有点均找到对应点为止；然后再利用对应点来求解刚体转换参数，本质问题就是求解对应点间的坐标转换参数，使得两点云集可以统一到同一坐标系的算法，实现点云表达的实物信息的融合，这样反复迭代就可完成匹配。常用的方法：单位四元数法和SVD正交分解法。

LZD算法的基本思想是：先以两表面上平面坐标相同的点位对应点(如果不存在就内插一个临时点)，然后利用对应点之间的Z坐标差(在DEM表面上就是高差)的平方和最小为原则来建立目标方程，最后根据最小二乘原理来求解转换参数向量，这组参数能够拉近两个表面。反复迭代上述过程，就可以正确完成匹配。

从上面的基本原理可以看出，两个算法匹配的框架基本相似，它们共同的算法流程如下：

1)建立两个表面上点之间的对应关系

(1)

其中，S={pi}为基准模型，M={qi}为待匹配模型；

2)根据对应关系，建立目标方程：

min∑wi‖pi-qi‖2.

(2)

3)根据不同的参数估计准则求解转换参数(ICP算法采用单位四元素方法求解，LZD采用最小二乘原理求解)

4)根据求得的转换参数更新待匹配模型；

5)判断匹配是否完成，若不满足条件，重复步骤(1)—(5)，直至满足迭代条件结束。

从上面算法流程可以看出，LZD与ICP算法的核心差别就在于它们处理表面对象的策略不同，这就导致了它们建立点对应关系的算法不同。ICP算法利用的是三维表面点的空间距离最近建立点对应关系，这使得该算法迭代收敛速度很快，但是由于其建立点对应关系的计算量大，从而导致整体计算效率不高，此外，该算法也有一定的局限性：

1)要求目标数据集和参考数据集要具有明显的特征，否则最终的匹配结果容易陷入局部最优；

2)目标数据集和参考数据集的对应近似点数要相等；而LZD算法是通过利用内插临时对应点的方法来避免复杂的搜索过程，其建立的关系较为粗略，计算量较小，但是当待匹配DEM对之间的姿态相差较大时，模型之间转换参数的初始值很难获取，所以完成匹配需要的迭代次数较多，严重影响了算法的迭代收敛速度和计算效率。

2 融合ICP和LZD的改进无控制DEM匹配算法

2.1 算法的实现

ICP算法的实质是基于最小二乘的最优匹配方法，重复进行“确定对应点集-计算最优刚体变换”过程，直到迭代误差足够小或迭代次数大于预设的最大迭代次数为止。ICP算法中经常用到的“点到点”的四元素转换参数法，其主要的求解步骤如下[15]：

1)计算基准DEM(标准模型)和变形DEM(待匹配模型)中任意对应点之间的距离(Di)(如式3)。

(3)

其中，(Xi1,Yi1,Zi1)为基准DEM中任意点的三维坐标，(Xi2,Yi2,Zi2)为待匹配模型DEM中对应点的三维坐标。

2)利用KD-Tree方法，在基准DEM中搜索与待匹配模型DEM的最近邻点集，然后构造协方差矩阵。

3)根据2)中的协方差矩阵构造4×4的矩阵Q，然后根据矩阵Q的最大特征值对应的特征向量计算旋转矩阵参数R，进而求得平移参数T(对初始变换参数进行更新)。

4)利用所求的旋转矩阵参数和平移参数对待匹配DEM进行更新，重复步骤2～4，直到迭代误差足够小(θ<ε)或迭代次数大于预设的最大迭代次数为止。

将ICP匹配算法得到的6个转换参数(尺度系数除外)作为LZD匹配的初始转换信息进行匹配，具体流程如图1所示。

基准模型与待匹配模型之间对应的数学转换关系(见式4)：

(4)

其中，(XR,YR,ZR)是参考DEM的坐标，(XT,YY,ZT)是对参考数据修改后待匹配DEM的坐标；ΔX,ΔY,ΔZ,S,R分别为两个DEM之间的平移参数、比例缩放系数和旋转参数矩阵。

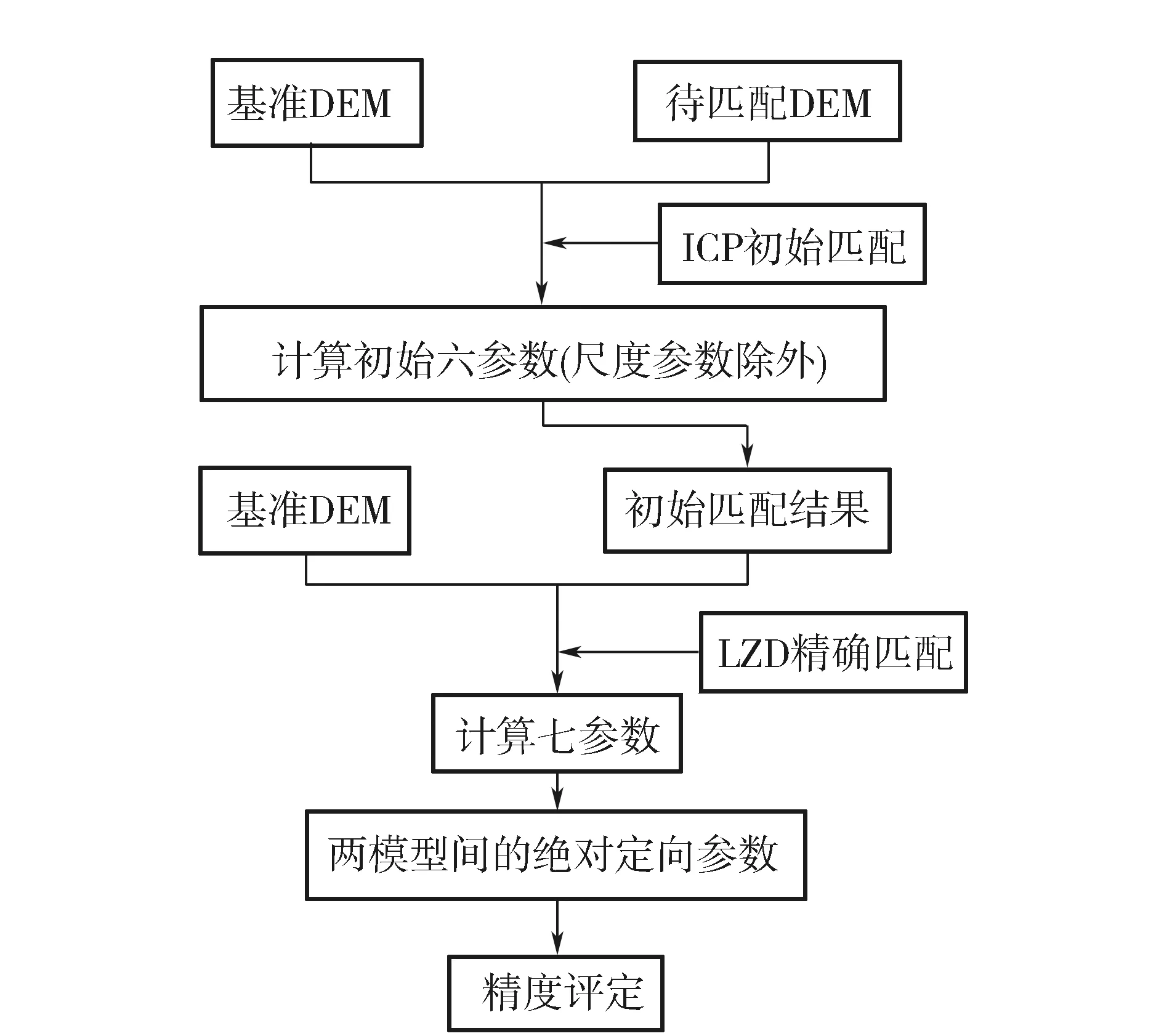
图1 匹配算法具体流程

利用ICP算法求解参考DEM和经处理后的待匹配DEM之间的变换参数，并通过式(5)对待匹配DEM进行坐标变换。

(5)

其中，(XR1,YR1,ZR1)是经过ICP算法匹配后，与基准DEM接近的第一组近似坐标；(X1,Y1,Z1)是修改后的变形模型DEM的坐标；ΔX1，ΔY1，ΔZ1和R1分别表示基准DEM与处理后的待匹配DEM经ICP算法匹配所得到的平移和旋转矩阵参数。

将经过ICP算法所得到的6个转换参数(尺度系数除外)作为LZD匹配的初始参数，再采用LZD算法进行精确匹配运算，并通过式(6)进行两模型间的转换。

(6)

其中，(XR2,YR2,ZR2)是经过LZD算法匹配后，与参考DEM对应的第二组近似坐标；ΔX2,ΔY2,ΔZ2,S和R2分别表示参考DEM与经过ICP算法匹配后的近似模型之间的平移参数、尺度系数和旋转矩阵。

将式(5)所得到的6个转换参数(尺度因子除外)作为LZD匹配的初始值，然后，通过式(6)迭代求解参考DEM和待匹配DEM之间的7个精确转换参数。因此，将式(5)、式(6)整理到一起可以得到最终的无控制匹配表达式(如式(7)所示)。

(7)

2.2 抗差最小二乘的引入

LZD匹配算法是通过参考模型与待匹配模型列立条件方程，根据最小二乘准则来求取模型之间转换参数的最优估计值，估计准则如下：

(8)

而LZD算法通过插值建立的同名特征点可能存在“伪同名点”(由于错误测量或遮挡等原因造成)，从最小二乘的估计准则可以看出，在平差过程中，异常值(即“伪同名点”)对残差平方和的影响较大，从而导致了最小二乘估计失去了对粗差的抵抗能力。文献[16]指出了最小二乘估计的BP值为1/n，即数据中仅有一个非常极端的异常值会对最后的平差结果产生非常恶劣的影响，故而不稳健。因此，需要引入抗差最小二乘的方法来抑制异常值对参数估计的影响，从而获得具有抗差性的参数估值。

Zhang等人[5]在LZD算法的基础上，引入高程差分模型，通过对不同点进行自适应加权，实现了DEM表面变形量的自动探测，可以探测到大于50%的表面形变。基本思路如下：在进行无控制匹配之前，将参与转换参数计算的非边缘高程点及其8邻域范围内的高程点按从左到右、自上到下的顺序进行排列。

2)将两模型间任一非边缘点的高差dZi与其8个相邻的高差均值dZm做差，得到(ΔdZ=dZi-dZm)，显然，每一个高程值Zi与ΔdZ是一一对应的。根据新的统计量ΔdZ对每一个观测值赋予不同的权值，以消除或削弱由于地表变形引起的匹配误差。规则如下：

(9)

其中，Med为中位数。

根据式(9)，每个观测值被赋予一个权0或1。只有权为1的观测值参与匹配，其余观测值在匹配过程中被剔除。通过上述方法进行确权，还存在很多孤立观测量，即其本身的权值为1，而其相邻的8个观测量的权为0，这是由于观测量中含有的表面变形被随机误差掩盖，用传统的最小二乘很难发现，但是可以很容易通过观测值之间的相互关系发现。通过对式(9)中的权值进行适当调整，将孤立观测点剔除，以提高最终的配准精度。

3 实验和结果分析

3.1 模拟实验

3.1.1 模拟实验数据的选择

为了对本文算法进行验证，试验数据采用张家界地区30 m分辨率的SRTM DEM数据为基础来设计模拟试验数据(如图2所示)。其优点在于理论上完全正确匹配的情况下，匹配完成后与仿真模拟变换前同名点处处重合，这样便于对本算法的实际试验结果进行准确的评价和分析。

1)基准DEM。以张家界地区的SRTM DEM数据为基础，格网间距为30 m，大小为128像素×128像素的子块作为基准DEM(如图2(a)图所示)。

2)模拟变形。

①对基准DEM在高程上添加0～2 m的随机误差；

②然后按表1参数表进行旋转、平移和缩放，产生与基准DEM对应的具有表面形变的待匹配模型。

表1 模拟转换参数表

3.1.2 模拟实验结果和分析

图2中分别为从张家界SRTM DEM数据中截取的初始DEM数据(称为基准DEM)和按表1中的转换参数所得到的具有变形的待匹配模型匹配前的分布图。分别采用基于四元素的经典ICP、ICP和LZD融合的算法，但是没有考虑表面形变进行自适应加权和采用差分模型进行自适应加权情况下的本文算法对基准模型和待匹配模型进行无控制匹配。

图3(a)为利用基于四元素经典ICP的配准效果图、图3(b)为ICP和LZD相结合算法的配准效果图、图3(c)是在ICP和LZD相结合的基础上，引入了差分估计模型的配准效果图。为了评定算法的配准结果，采用算法完成配准的迭代次数、完成迭代时间和平均误差对比，在理论上完全正确匹配的情况下，匹配完成后与模拟变换前的点与点处处重合，因此，本文选择将迭代结束后各对应点间配准的残差平均值即“平均误差”作为评定标准。

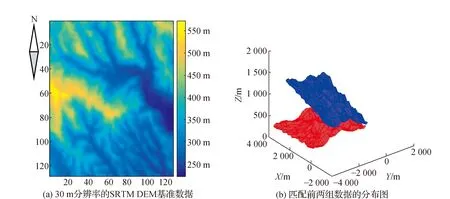
图2 初始DEM数据和匹配前的分布图(红色:基准DEM;蓝色:变形DEM)

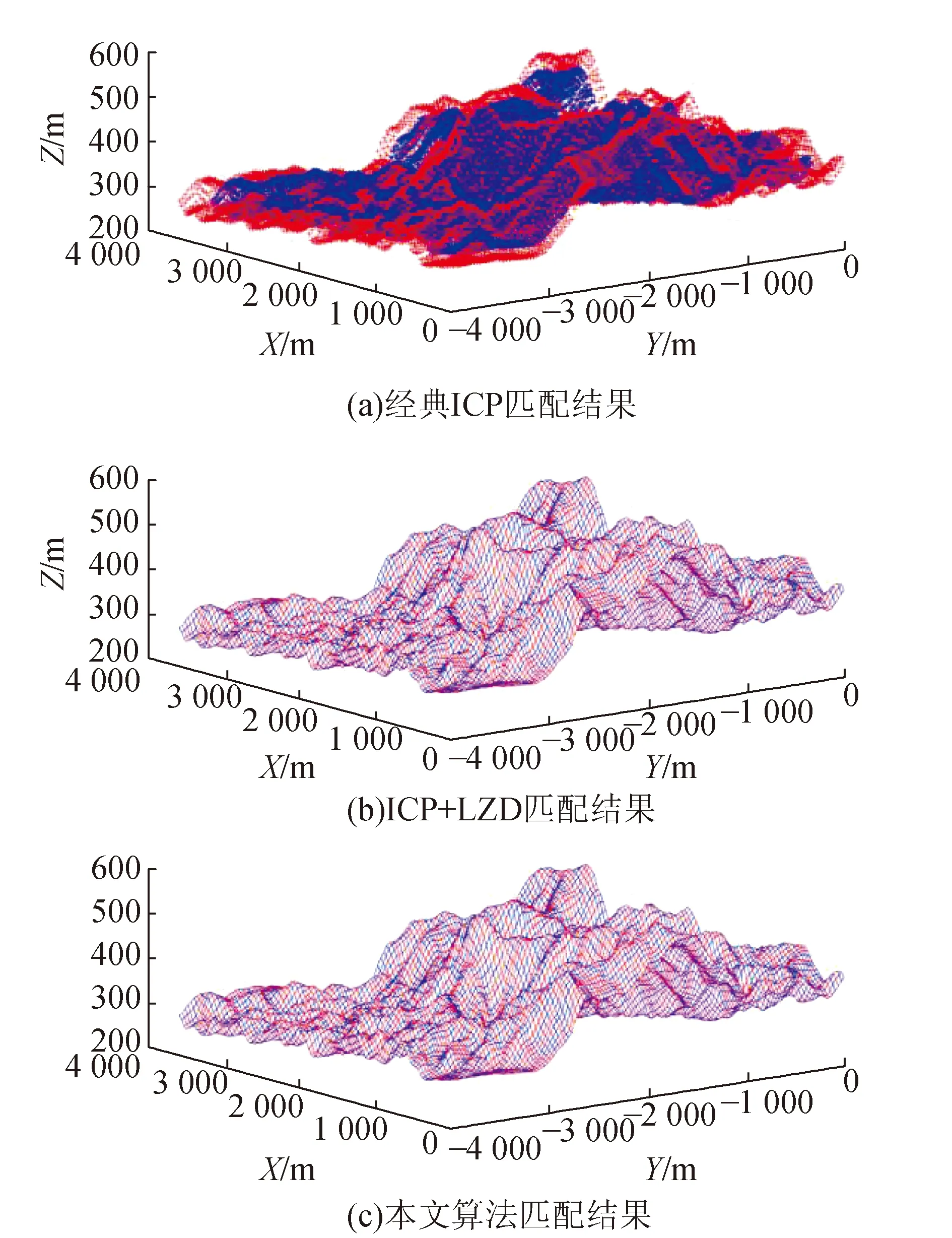
图3 不同匹配方法的点云数据(红色:基准DEM点云数据;蓝色:配准后的DEM点云数据)

从图3中的匹配效果图可以看出，传统的经典ICP算法(图3(b))，对于有尺度变换的DEM数据无法完成正确的匹配，匹配后的平均误差也较大；但是在ICP的基础上引入LZD算法(图3(b))，可以实现有尺度变换的数据之间的匹配，且与本文算法(图3(c))的匹配效果图很接近，但是，表2中给出的迭代次数、完成迭代的时间和平均误差的对比，可以看出，本文算法不仅比传统的ICP算法得到了更精确的配准结果，并且与单一的LZD匹配算法相比，其配准的收敛速度和精度得到了大幅度的提高。此外，表3给出了不同算法匹配后所得到的模型之间的转换参数与模拟参数之间的误差比较，可以看出：经典的ICP算法对存在尺度变换的数据进行匹配时，效果最差；而LZD算法与ICP和LZD相结合的算法最后的匹配精度相当。这是由于这两种算法匹配精度都是由LZD算法所决定，ICP算法只是起到加快收敛速度的作用。本文是是在最小二乘的基础上引入了差分模型，所求的是转换参数的抗差解。虽然本文算法相较于ICP+LZD算法在x，y轴平移参数上精度稍差，但是对高程和三轴旋转参数的估计较精确，而旋转参数误差(乘性误差)与平移参数误差(加性误差)相比， 前者对最后匹配精度的影响更大。因此，即使图3(a)和图3(b)在主观视觉上效果很接近，通过转换参数误差和平均误差的对比，本文算法更优。

本文算法匹配过程中，引入差分模型对高程点进行自适应加权处理，求得转换参数的抗差解，很大程度上消除或削弱了由于地表形变(随机误差)所引起的配准误差，使配准后的平均误差由1.6 m提高到了0.7 m。实验结果表明，本文算法不仅可以顾及两组数据之间的尺度变换参数，且能够削弱多时期数据之间的地表形变对配准结果的影响，具有较快的收敛速度和较高的配准精度。

3.2 无控制DEM匹配的应用

3.2.1 实验数据

为了评价全球DEM数据的精度，通常需要将其与我国现有的地形数据转换到同一坐标系下，保证数据之间具有相同的数学基础，而投影转换所需要的平移、旋转和缩放系数属于国家保密数据，仅仅通过现有的商业软件并不能使两组数据完全重叠，因此需要通过七参数转换对预处理后的数据进一步校正。试验数据为张家界地区的参考DEM数据和2003年获取美国国家航空航天局(NASA)发布的SRTM1 DEM数据。图4中分别为参考DEM数据和经过预处理后的SRTM1 DEM数据，格网间距均为30 m，数据大小均为128像素×128像素，且存在一定的重叠区域，由于获取手段和地形条件问题，很难通过在图上直接选取同名控制点进行数据之间的投影转换，因此只能采用无控制DEM匹配方法将两组数据转换到同一坐标系下。

表2 DEM配准迭代次数和精度对比

表3 不同匹配方法的参数误差对比

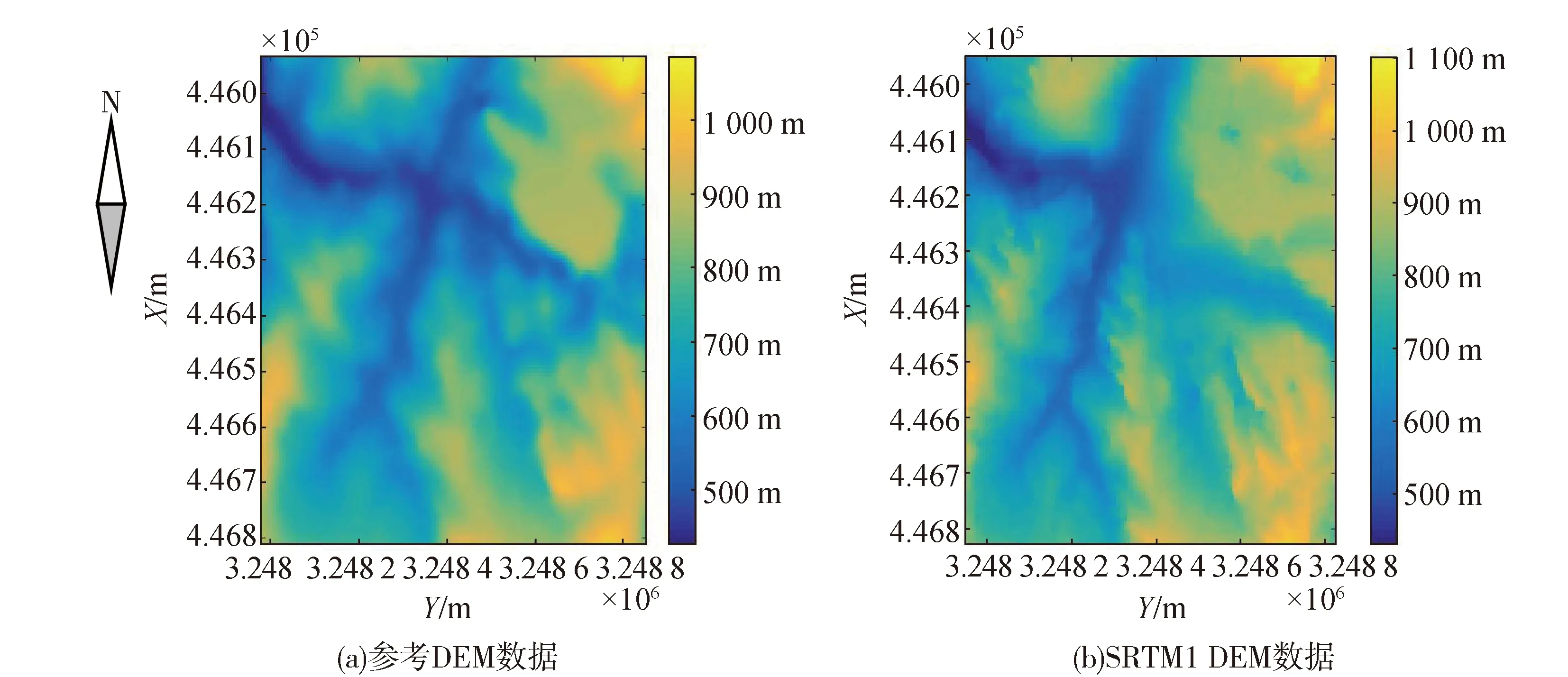
图4 张家界试验区DEM数据

从图5(b)可以看出，在没有进行精确配准之前，两组数据的等高线之间存在着明显的不重合，两组数据之间存在着一定的旋转、平移等转换关系。为了验证本文算法的实用性和可靠性，分别采用LZD算法和引入差分模型的本文算法对两组DEM数据进行无控制匹配。

3.2.2 实验结果

依据不同匹配算法得到的两组DEM数据间的7个转换参数，将SRTM1 DEM自动转换到与参考DEM数据同一坐标系中，匹配后的两个DEM的点云效果图和等高线图如图6所示。从匹配后的点云效果图来看，采用无控制DEM匹配方法基本上可以将两组数据配准到同一坐标系下，两种算法的匹配效果很接近；但是通过匹配后的等高线图可以看出，采用本文算法所得到的两组数据等高线总体吻合程度优于仅采用LZD算法的匹配结果。此外， SRTM1 DEM是通过雷达方式获取的，考虑到合成孔径雷达成像的特点，在地面起伏度较大的地区该DEM存在明显的异常[17]，如图6区域A和区域B所示。仅采用传统LZD算法进行无控制匹配，不仅收敛速度很慢，由于异常数据的影响，无法获取较精确的匹配结果；引入差分模型后的本文算法，降低了粗差(异常)点对配准结果的影响，从而使经过匹配后的两组等高线数据重叠度较高，匹配结果更加准确、可靠。从匹配时间上看，LZD匹配算法需要迭代28次，时间消耗136 s，而本文算法只需要迭代8次，时间消耗39 s，收敛速度提高约70%，匹配效率更高。

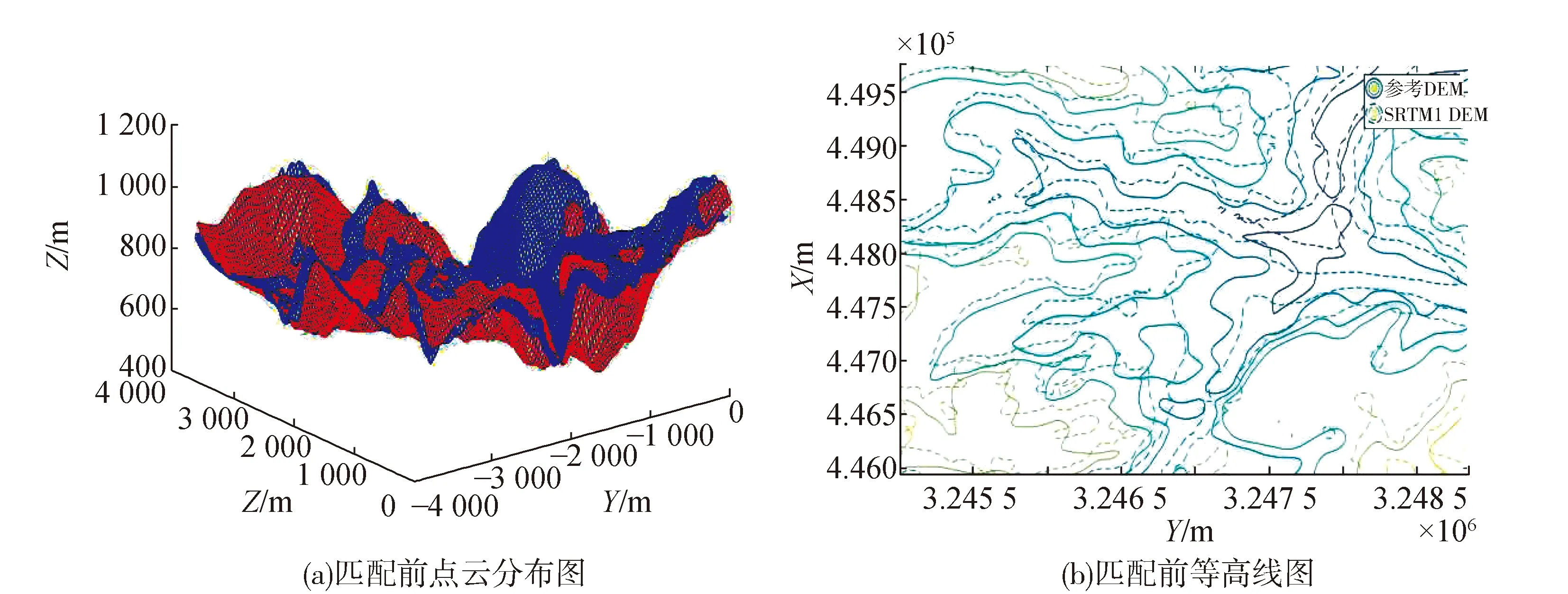
图5 参考DEM和SRTM1 DEM匹配前点云和等高线图

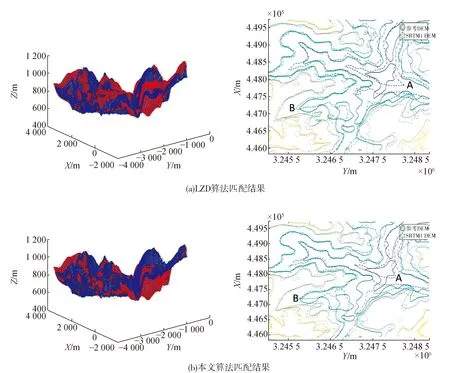
图6 不同算法匹配后点云效果图及等高线比较图

4 结 论

本文改进的无控制DEM匹配算法，首先通过经典ICP算法进行初始配准，并将所获取的初始转换参数(尺度参数除外)作为初始值，进一步采用LZD算法进行精确配准，提高了LZD匹配算法的收敛速度；此外，由于传统最小二乘估计不具有抗差性，本文引入高程差分估计模型，在迭代过程中对不同精度的高程点进行自适应加权处理，消除或削弱了由于地表形变所引起的配准误差，从而保证了算法的精度。依照实验结果和对比分析可知，改进后的算法在配准效率、配准精度上较传统算法都有大幅度的提高。最后，将本文算法应用于SRTM1 DEM与参考数据的无控制匹配实验中，可以获得较好的匹配结果，其匹配结果可以为DEM数据质量的评价和多源DEM数据的融合提供较好的基础数据。

LZD算法是通过最小化三维表面所有对应点间的高差平方和来求解表面转换参数，随着DEM数据的全球化和多源数据的发展，为了将本文算法的配准结果应用于大范围多源、多时相DEM数据的融合中，后续工作将在本文算法的基础上，结合特征点检测的思想对大范围DEM数据之间的配准工作进行研究，并对其做进一步的完善。