不等偏距RCCR舵机执行机构的研究*

杨 震，宋梅利，王晓鸣，杜英杰

（南京理工大学智能弹药技术国防重点学科实验室，南京 210094）

0 引言

弹道修正弹舵机的工作原理是依靠安装在弹上的舵翼，在控制系统的信号下进行偏转，利用其在空气中产生的气动力改变弹丸飞行的速度和方向，进而实现弹道的修正［1］。因为修正弹空间体积小、弹翼偏转角度大、启动力矩有限，所以极大地限制了舵机执行机构的发展，寻求合适的执行机构是舵机设计的重要环节。国内学者王俊全设计了一种四轴联动电动舵机，执行机构由定向杆、旋转架等组成［2］；孟庆宁通过二级齿轮的方式将电机驱动传递至舵轴［3］；葛明设计的执行机构包括滚珠丝杠和RSSR空间连杆机构［4］；目前国内所设计的舵机，执行构件数目偏多，传动机构复杂，能否在弹道修正弹上高效工作还有待研究。

空间RCCR机构具有结构简单、低副连接、耐磨性好、便于制造、输入轴和输出轴轴线夹角取值范围大等特点。近年来，国内学者对等偏距条件下的RCCR结构进行了大量的研究。庄森教授、张开飞对同转向RCCR机构的运动规律进行了探讨，得出了传力杆铰接点的运动轨迹是椭圆等结论［5］；庄森教授、虞启辉对RCCR机构考虑运动副摩擦力时的受力情况进行了有益的探索［6］。而对于不等偏距RCCR机构的认识，国内学者仍停留在其旋转-摆动的输入输出关系上，经初步研究，发现此运动特性满足了舵机执行机构的需求，因此，本文对不等偏距形态下的RCCR机构进行了更为充分的理论研究与仿真验证，为其在舵机上的实际应用提供可靠的理论基础。

1 RCCR机构的运动分析与基本参数设计

如图1所示的空间RCCR机构，由输入轴1、输出轴4、固联传力杆5、圆柱副B、圆柱副C、两个固联在机架上的转动副D、E构成，并将固联传力杆沿固定处A点分为杆件2，3，以便后文中的研究。定义如图 1 所示的结构参数 L1、L2、h1、h2、α 和运动参数s1、s2、θ1、θ2。根据各运动参数在 xy 坐标平面上的投影求解可得［7］：

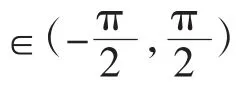
2 机构的静力分析

对机构静力分析的目的在于确定各运动副中约束反力、反力矩和原动件上的平衡力矩，为零件的强度计算、机械效率的估算和研究磨损、润滑等问题提供基础［8］。注意到RCCR机构含有两个圆柱副B、C和两个转动副D、E，另外在机构的原动件上还加载了一个启动力矩，因此，独立分量个数共有19个；而该机构有3个运动构件，对各个构件分别建立力、力矩平衡方程，可列出18个独立的线性方程。因此，RCCR机构为静不定结构，需联立变形协调方程才能求解出所有未知力和力矩［9］。

输入轴1在驱动转矩M的作用下，以角速度作无摩擦匀速转动，当机构运转速度较低时将忽略各构件的惯性力。如图3所示，将RCCR机构分解为a、b两个部分。由于杆件2、3均含有沿自身轴线转动和移动的自由度，结合力与反力的关系分别对两部分建立平衡方程：

传力杆2、3两侧轴线分别与两圆柱副轴线重合，因此，拐点A处在固联传力杆5相交轴线所确定平面沿两轴线角平分线方向的挠度为0。根据材料力学知识可得［10］：

化简式（3）得到构件的补充方程：

联立式（2）～式（4）整理可得：

以圆柱副B为例，列出受力平衡方程组，求解后可得：

采用同样方法可以求解出RCCR机构中圆柱副C、转动副D、E处的约束反力和约束力矩，这里不再叙述。

3 RCCR的刚柔耦合分析

为了分析关键部件在受载变形时RCCR机构的动态特性以及验证静力学计算结果，本文将传力杆视为柔性体，结合ANSYS软件和ADAMS软件建立刚柔耦合模型。首先利用ANSYS软件生成模态中性文件，并将其导入ADAMS中，替换多刚体模型中的传力杆，完成刚柔耦合模型的建立。模态中性文件与刚柔耦合模型如图4、图5所示。在建模过程中需要注意的是，滑移副或平面内运动虚约束不能直接加在柔性体上，解决这个问题的方法是创建一种哑物体（Dummy Part），其质量、转动惯量均为0，通过哑物体建立柔性体与其他构件之间的连接关系［11-12］。设置输入轴转动参数为1 800 d*time，仿真时间为0.4 s，设置步长为4000。具体约束类型见表1。

表1 RCCR刚柔耦合模型的约束类型

图6和图7分别为圆柱副B约束反力、反力矩的仿真结果。以圆柱副B为例，可以看出，刚柔耦合模型在运动的开始阶段，反力与反力矩有很大的波动。这是由于运动激励的突然施加，机构受到柔性体弹性变形的影响，运动不平稳。随后数值恢复稳定，曲线平滑，随正弦规律变化。从表2各运动副最大约束反力与反力矩可以看出，该机构受力状况良好，可以满足舵机执行机构的刚强度要求。

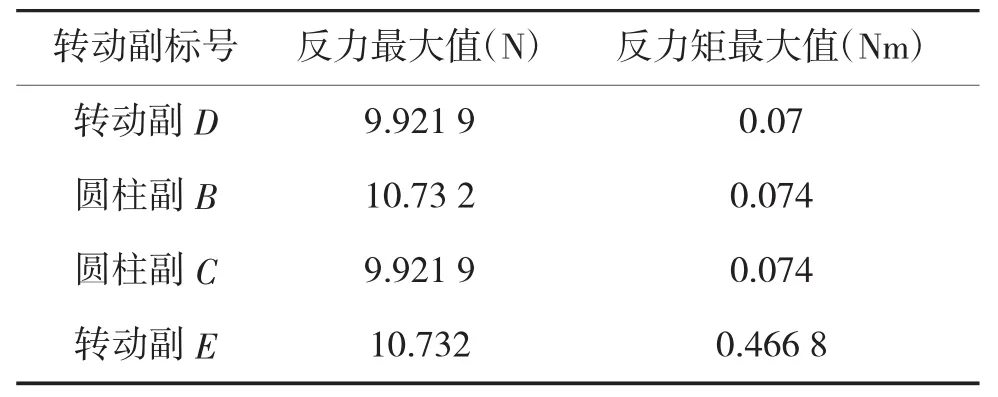
表2 各运动副最大约束反力与反力矩

4 理论计算与仿真分析的对比拟合

通过编写Matlab程序，将理论计算与刚柔耦合模型的仿真结果进行对比，在拟合过程中去除了启动阶段的波动干扰。其中圆柱副B的约束反力与反力矩的拟合分析结果如图8、图9所示：

以圆柱副B在Z轴方向上的约束反力矩M12z为例，可以看出仿真值与计算值之间存在着一定的误差，出现误差的主要原因有：柔性件的弹性形变所造成的运动副变形；柔性体构件有限元模型的集中载荷和节点载荷之间的相互转化造成了力矩的数值误差；以及忽略了惯性力和杆件外形所造成的误差。通过计算拟合优度，得到R2=0.921 1，说明了理论模型和仿真模型的拟合程度较高，证实了该刚柔耦合仿真模型的有效性。

5 结论

本文对不等偏距条件下的空间RCCR机构进行了运动和力的理论计算，以及刚柔耦合仿真，探索了该机构应用在舵机执行机构上的可能性，得到了以下结论：1）不等偏距RCCR机构的输出最大摆角取决于h1与h2的比值。设计h1=13.7 mm，h2=40 mm，输入轴1连续整周旋转时，输出轴输出±20°的摆角。2）建立的RCCR的静力学理论模型计算结果与刚柔耦合模型计算结果高度一致，证实了该刚柔耦合仿真模型的有效性。3）不等偏距条件下的RCCR机构结构简单、偏转角度可控、受力状况良好，其在弹道修正弹舵机上应用具有一定优越性。