基于随机矩阵特征值差的频谱感知改进算法*

高 鹏，刘芸江，高维廷，陈 娟，李 曼

（1.空军工程大学信息与导航学院，西安 710077；2.解放军91917部队，北京 100000；3.西安航空学院，西安 710077）

0 引言

频谱感知作为认知无线电（Cognitive Radio，CR）的关键环节，通过实时检测频“频谱空穴”（White Space），实时、准确地判断主用户（Primary User，PU）的授权频率资源是否空闲，可供认知用户（Second User，SU）接入使用，被公认为是解决目前频谱资源紧张的重要技术［1］。

目前，现有的频谱感知算法主要有：匹配滤波检测、循环平稳特征检测、能量检测、多用户协作检测等［2］。匹配滤波［3］要求主用户信号先验，以此设计滤波器机构，不符合应用实际；循环平稳［4］特征检测性能较好，但计算复杂高、实时性差；能量检测［5］简单易实现、对主用户信号非先验，但其性能受噪声不确定度影响大，存在着信噪比门限要求。利用MIMO［6］、数据融合［7］、双门限判决［8］等技术的多用户协作检测近年来得到了一定的发展，但基于能量检测的本质仍无法克服噪声不确定性带来的影响。

本文结合文献［9-13］的思路，以特征值均值与最小特征值之差构造检测统计量，提出了一种改进算法DAM，在此基础上分析讨论基于Tracy-Widom分布与基于正态分布两种门限选取方式，理论与仿真结果表明，该算法检测性能在低采样、低信噪比下较现有DMM、ME-S-ED算法有所提升。

1 系统模型

1.1 实际频谱感知场景

如图1所示，在认知无线网络中［1］，主用户（PU1，PU2，PU3，…）通过主基站（Primary Base Station，PBS）进行通信；认知用户（SU1，SU2，SU3）协同检测PU信号，将检测数据送至次级基站（Second Base Station，SBS）进行数据处理，判断PU授权频段是否存在频率空穴可供SU使用。

1.2 频谱感知模型

采用认知无线电中经典的二元假设数学模型［1］，假设在窄带的认知无线电网络中，只存在一个主用户，认知用户对其信号进行检测判决，描述如下：

其中，H0与H1分别代表主用户信号存在与不存在的情况，xi（n）为第i个认知用户接收到的采样信号，si（n）与ωi（n）分别为待测主用户信号和干扰噪声，hi（n）为信道衰落因子。不失一般性，假设如下：1）干扰噪声为高斯白噪声，并且服从；2）主用户信号si（n）幅值服从均值为μ方差为σ2的高斯分布，且与噪声相互独立；3）M个认知用户检测一个主用户的同一频段；4）在检测期间，信道特性稳定，hi（n）保持不变。

对于M个认知用户采样N次，多用户协作频谱感知模型可以概括为：

认知用户采样信号协方差在采样数N较大时，近似表示为：

R（xN）的特征值近似表示为，ρi为RHs（N）的特征值为的均值。

在H0成立时，只存在高斯白噪声个特征值均为σ2，满足；

在H1成立时，因s（n）自身不同采样时刻具有相关性，ρi使得i间不再相等，此时；

Rx（N）的特征值统计均值，在主用户信号存在时的差异性为检测提供了可行性思路。

2 DAM频谱感知算法

2.1 算法理论基础

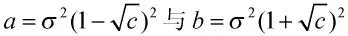
定理2当信号为实信号时，满足［15］：

2.2 检测门限推导

基于在H0与H1不同情形下的差异性，选取作为检测统计量，在理想状况下，无主用户信号时的值为0，考虑虚警概率下表示如下：

γDAM为判决门限，γDAM的取值影响着检测性能的优劣。在同一检测统计量下，门限较低者检测性能更好，TDAM作为差值结构，存在着2种半渐进门限的选取方式，如下：

1）γ1：选取作为统计分布，在H0时min的近似值下计算；

2）γ2：选取min特征极限分布，在H0时的近似值下计算。

γ1具体推导方式如下：

DAM算法虚警概率表示为：

其中，Q（x）为概率积分函数，满足表达式：

γ2具体推导方式如下：

根据定理2，利用最小特征值的极限分布，

得到

其中，F-11（t）为一阶Tracy-Widom累计分布函数反函数，F1（t）闭合表达式仍未得到，文献［17］通过数值计算方法得到750点F1（t）与F-11（t）离散图像，如图2，常用数据如表1所示。

表1 一阶Tracy-Widom累计分布函数部分数值点

两种门限值的选取将影响着DAM算法的检测性能，方便分析记为DAM1与DAM2，具体将在下一节中分析比较。

两种不同推导方式下的门限值，均与噪声能量有关，利用DMM算法中的特征值噪声估计法［11］，，对噪声进行实时地估计，保证判决门限的相对准确性；同时差值结构的检测量，特征值相减抵消了噪声不确定性带来的影响。

2.3 算法步骤

DAM算法步骤概括如下：

1）对检测信号采样，计算待检信号的协方差矩阵Rx（N）；

2）求取Rx（N）的所有特征值，计算其均值，并构造统计量

3）利用特征值噪声估计法对噪声方差进行实时更新；

4）利用更新后的噪声计算判决门限γ1与γ2；

5）进行判决，累计次数，计算检测概率。

3 仿真结果与性能分析

3.1 门限比较与分析

假设不存在主用户信号，只输入高斯白噪声验证算法门限的有效性。在认知用户数M=5，虚警概率Pfa=0.1时，在不同采样点数N的情况下得到检测统计量-min与两门限γ1与γ2的关系，如图3所示。

从中得到，在低虚警概率时，两门限数值非常接近，但门限γ2值较门限γ1更低，随着样本数目逐渐增加，二者差距越来越小；γ1与γ2均高于实际检测量，因虚警概率的存在，只有少数点越过了γ2，证明了两种推导方式的有效性。

同时，采用最小特征值极限分布得出的γ2比正态分布下得出的γ1更低，意味着更好的检测效果；γ2距离实际量较远，用检测性能“换取”了低虚警概率，不利于实际检测效果。仿真结果证明了虽然没有闭式表达式的Tracy-Widom分布比正态分布更贴近实际检测。

3.2 算法性能比较与分析

假设主用户信号为QPSK信号，经过2 000次Monte-Carlo仿真实验，在设定虚警概率Pfa下，以统计检测概率Pd为指标，与DMM算法、ME-S-ED算法进行比较。

图4为在虚警概率Pfa=0.05，认知用户数M=5时，采样点数为1 000时，检测概率与信噪比的关系。从图中得到，随着信噪比的增加，算法的检测概率均迅速上升，采用门限γ2的DAM2增速最快，在信噪比-14 dB时已经接近了90%，其次为DMM算法，DAM1与ME-S-ED算法的增速则相对较慢，原因在于在相对低采样的情况下，利用特征值均值改进检测量等同于降低了检测量数值的大小，间接地降低了对门限的敏感性。

但在低信噪比的情况下DAM1与ME-S-ED算法较优，在-20 dB时的检测概率能够高于DAM2与DMM算法10%，原因在于DAM2与DMM基于特征极限分布，而特征值均值近似于平均能量，在低信噪比下其能量特性使其仍保持一定的检测性能。

图5为在虚警概率Pfa=0.05，认知用户数M=5，信噪比为-20 dB时，检测概率与采样点数的关系。旨在验证在图4低信噪比的情况下，通过增加采样点数对检测性能的影响。可以得到，随着采样点数的增加，低信噪比下的检测性能均得到了提升，且优于原DMM算法。其中，利用特征值均值改进的DAM1与ME-S-ED比利用特征值极限分布的DAM2与DMM上升更快，在采样点数为5 000时，DAM1检测概率可以达到95%，原因在于低信噪比时，主用户信号微弱，此时利用特征值差异性的检测方式相较于利用能量差异，在分解近似中降低了敏感性；DAM2的检测性能仍优于DMM，原因在于，最小特征值的极限分布在低采样时相较最大特征值极限分布更为准确，随着样本不断增大，差异性渐渐减小。

图6为在虚警概率Pfa=0.05，采样点数为1 000，信噪比为-20 dB时，检测概率与认知用户数的关系。旨在验证，在图4、图5低采样、低信噪比的情况下，增加参与协作的认知用户数对检测性能的影响。随认知用户数量的增加，算法的检测性能均上升，且均优于原DMM算法；采用特征值均值改进的DAM2与ME-S-ED要优于DAM1。原因在于特征值均值利用了所有特征值，涵盖的矩阵特征信息要明显于其中一个特征值，更能体现矩阵的“特征”，随认知用户数增加，特征值数量增加，特征值均值优势凸显。

图7为在采样点数1 000，信噪比为-20 dB，认知用户数M=5，在不同虚警概率下的工作特性（Receiver Operating Characteristics，ROC）曲线图。旨在总结算法在上述图4～图6的低采样、低信噪比情况下的综合性能。随虚警概率的增加，DAM1增长最快，在30%的虚警概率下可以达到96%；综合表明了在同时低采样点数、低信噪比的情况下，DAM1与DAM2性能更优。

仿真结果表明，两种改进算法在低采样、低信噪比的情况下，相较于原DMM和现有ME-S-ED算法均有一定的性能提升；同时，只在低信噪比时DAM1略有优势，而只在低采样时DAM2更有优势。

4 结论

本文在随机矩阵特征结构理论上，在DMM算法的基础上提出了一种特征值均值与最小特征值之差的频谱感知改进算法（DAM），并在此基础上分析讨论了DAM算法在两种门限下的检测性能（DAM1与DAM2）。理论分析与仿真表明，该算法在几乎不增加算法复杂度的同时，在低采样、低信噪比的情况下，比DMM算法以及现有ME-S-ED改进算法具有更好的检测性能。