固体火箭复合推进剂平均侵蚀函数的预测方法与应用

陈 军

(南京理工大学 机械工程学院,江苏 南京 210094)

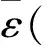
本文以文献[1]建立的火焰弯曲理论侵蚀函数方程为基础,发展了一种能够预测AP固体复合推进剂平均侵蚀函数的理论方法,并进行了算例验证。

1 固体火箭复合推进剂平均侵蚀函数预测的理论模型

以火焰弯曲理论为基础,文献[1]给出了固体火箭复合推进剂的火焰弯曲理论侵蚀函数方程,即

[(K3p2)2-1]m2ε6+[2(1+K2)m-m2b2-2m(K3p2)2]ε4+[(K3p2)2+2(1+K2)mb2-(1+K2)2]ε2-(1+K2)2b2=0

(1)

燃气流速v是影响侵蚀燃烧的主要因素,文献[1]以方程(1)为模型,研究了固体火箭复合推进剂ε-v的变化关系,从而得到侵蚀函数ε(v)。该侵蚀函数主要应用于一维内弹道计算。分析方程(1)可知,该方程综合考虑了燃气流速v、压强p、推进剂性质等因素对侵蚀的影响。由固体火箭发动机原理可知,燃通比反映了这种综合关系[6]:

(2)

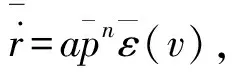
设ε(v)=α+βv,其中,α,β为待求系数,则速度平均侵蚀函数为

式中:Lp为固体火箭推进剂的装药长度,x为发动机轴向坐标。

一般地,燃气流速v-x需要通过求解一维内弹道来获得。为简化计算,不妨设:

(3)

则

(4)

故有

(5)

式中:v2为装药末端的燃气流速,可通过气体动力学关系J=q(λ)来计算[7],其中,J为喉通比,q(λ)为气体动力学函数,λ为速度系数。

(6)

式中:π(λ2)为气体动力学函数,λ2为装药末端的燃气流速系数。因此,装药末端的燃通比2为

(7)

2 侵蚀函数ε()的求解

获得系数K1,K2,K3,可以直接利用MATLAB求解一元三次方程函数roots(·)的方法求解火焰弯曲理论侵蚀函数方程(1)[1,8]。与文献[1]不同的是,这里需要考虑压强的影响,并求出对应的燃通比。

ε()=0.981 5+0.003 808+0.000 002 9892

(8)

表1 求解得到的不同燃通比(末端)的侵蚀函数值

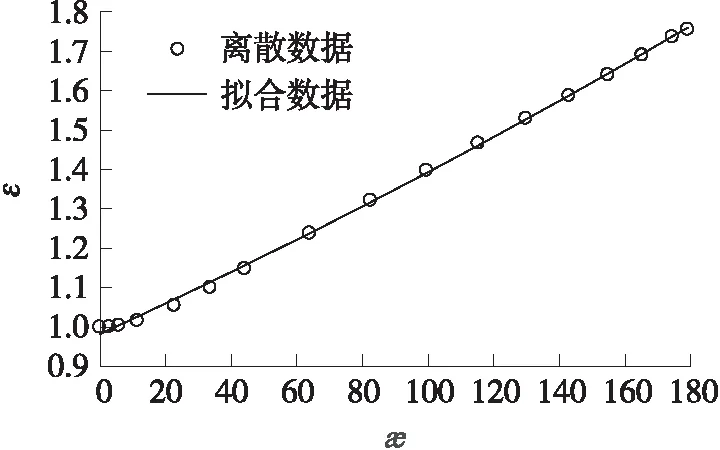
图1 拟合得到的侵蚀函数ε()曲线与离散数据的比较

3 平均侵蚀函数的计算

由固体火箭发动机原理知,通过对侵蚀函数式(8)进行平均,即可得到平均侵蚀:

(9)

以某中口径固体火箭推进剂为例,已知其平均侵蚀函数为

(10)

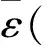
(11)

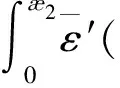
(12)

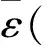
(13)

图2为预测的侵蚀函数式(13)与原侵蚀函数式(10)的对比曲线,由图可见,二者符合度较好。取该火箭发动机的最大,即=155.5,此处误差最大,预测的侵蚀比为1.404 9,原侵蚀比为1.387 5,相对误差为1.3%,满足一般工程的精度要求。

图2 预测的平均侵蚀函数与原侵蚀函数的比较

4 预测平均侵蚀函数的应用分析

上述过程可以完全确定固体火箭复合推进剂的平均侵蚀函数。为验证该方法的通用性,下面以不同于前述口径的火箭发动机为例来进一步计算和分析。

1)侵蚀函数ε()的求解。

首先按文献[1]的方法拟合得出所研究固体火箭推进剂燃速公式中的系数K1,K2,K3。计算得出该小口径火箭发动机K1=0.763 2,K2=19.908 9,K3=0.106 1。获得系数K1,K2,K3后,直接利用MATLAB的roots(·)函数求解火焰弯曲理论侵蚀函数方程,得出不同燃气流速下ε-数据点,最后拟合得到ε-的变化关系:

ε()=0.982 9+0.002 778+0.000 002 1712

(14)

对式(14)平均,可得平均侵蚀函数:

(15)

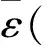
(16)

将预测的侵蚀函数式(16)代入该火箭发动机的内弹道模型,计算曲线如图3所示,图中,t为工作时间。实验数据与预测数据的比较如表2所示,表中,e为相对误差,p0为初始压强,pmax为最大压强。由图3、表2结果可见,预测侵蚀在初期偏小,但相差很小,精度较好,满足一般工程精度要求。

图3 某固体火箭发动机压强预测值与原始数据曲线的比较

表2 利用预测平均侵蚀函数计算的某固体火箭发动机工作压强与实验数据的比较

5 结论

通过对某中口径复合推进剂的建模、对某小口径复合推进剂的应用分析,本文研究结果表明,利用火焰弯曲理论预测平均侵蚀函数的方法是可行的。该过程步骤如下:①求解侵蚀函数ε()。首先回归出火焰弯曲理论燃速公式的系数K1,K2,K3,再求解火焰弯曲理论侵蚀函数方程,得出不同燃气流速时ε-数据点,拟合得到ε()的变化关系。②求解预测平均侵蚀函数)。首先对ε()求平均,得到平均侵蚀函数),然后采用曲线积分面积相等的原则进行变换,得到最终形式的平均侵蚀函数)。

在使用该方法时,文献[1]中有关修正系数、尺寸效应的应用规律同样适用,且保持数值不变,这说明火焰弯曲理论在预测固体复合推进剂的侵蚀函数方面具有比较好的规律性与合理性。另外,本研究只是针对AP复合推进剂,是否适用于其他推进剂还需要进一步研究。