基于改进自适应算法的四旋翼飞行器姿态控制

张釜荣, 谢慕君, 武凡凯

(长春工业大学 电气与电子工程学院， 吉林 长春 130012)

0 引 言

随着人们对物质文化的要求不断提高，科学文化发展更新换代，机器人的应用在日常中越来越普及和至关重要，其中四旋翼飞行器是机器人领域的一个重要分支。

近几年，四旋翼飞行器在工业和人们的现代生活中起到了越来越广泛的应用，特别是在一些较为危险的领域，如森林火灾监测、交通监管、救灾等，无人机规模小、操作简单、结构灵活。 在狭窄的空间中，垂直起飞和着陆、翻转、前进和后退等特征起着突出的作用。

四旋翼的姿态在飞行轨迹中起着重要的作用[1]。针对四旋翼飞行器姿态控制问题，国内外许多学者提出了多种非线性和线性控制器设计方式，如PID(Proportion Integration Differentiation)控制[2]、滑模控制[3-5]、反步控制[6]、线性二次高斯控制[7]、H∞控制[8]、自适应控制[9]等。文中对自适应控制方法进行改进，提出了自适应鲁棒滑模控制方法，采用自适应控制方法对未知参数变化的不确定性进行估计，采用滑模控制方法对有上界的外部干扰进行抑制，为验证算法的有效性和准确性，文中在Matlab/Simulink环境下进行数值仿真。

1 四旋翼的动态模型

采用一个四输入、三输出的四旋翼飞行器，动力由装配在万向节轴杆上的4个带螺旋桨的电机供给。

1.1 建立三维坐标系

四旋翼飞行器如图1所示。

图1 四旋翼飞行器力学坐标

其中，支撑点为坐标原点，x轴为指向前方电机的轴，y轴为指向右侧电机的轴，尾部电机转动牵引螺旋桨运动形成与y轴同向为正方向的力。z轴正方向由x轴方向和y轴方向确立，正前方、左、右电机转动驱动螺旋桨运动产生与z轴同向为正向的力。其中Ff为前方向电机提供的力，Fl为左侧电机提供的力，Fr为右电机提供的力，Fb为尾部电机的作用力[10]。

1.2 四旋翼飞行器动力学方程

在输出姿态角的力矩平衡方程中，做出以下假设：

1)假设系统处在静平衡状态，所有的姿态角均为零；

2)忽略电机阻尼力矩；

3)忽略电机达到给定转速的时间；

4)假设螺旋桨正转时产生的力与反转时产生的力是相同的。

四旋翼动力学模型:

(1)

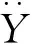
Lf——前向螺旋桨中心到y轴的距离;

Uf，Ul，Ur,Ub——分别是前向、左侧、右侧和后向电机的输入电压;

JP，Jr，Jy——分别为四旋翼飞行器绕y、x、z轴旋转的转动惯量；

Kfc——正常数。

四旋翼飞行器的前方电机与左右两侧电机的控制量之间存在耦合，如下：

Ur+Ul=Uf

(2)

可以根据俯仰、滚转、偏航通道选取输入向量如下：

(3)

其中：

(4)

飞行器的模型参数见表1。

表1 飞行器的模型参数表

将式(1)简化得到：

(5)

即

(6)

其中，J是系统变化未知的转动惯量，则取不确定参数β对转动惯量进行实时逼近。考虑模型不确定部分和干扰的总体不确定性，取β=J，式(6)可写为：

(7)

式中：Δ1，Δ2，Δ3——干扰和模型不确定部分的总体不确定性。

对上述方程做出如下假设：

假设1 不确定参数β的上下界定义为：

β∈Ω≜{β:0<βmin≤β≤βmax}

(8)

假设2 不确定项Δ有界，表示为：

|Δ(1,2,3)|≤D

(9)

2 姿态控制器的设计

设系统模型状态变量为

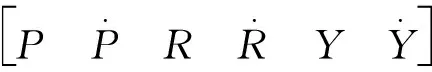
(10)

可以将式(7)写成如下形式：

(11)

针对俯仰角控制率的设计，假设位置跟踪误差为:

e=x1-xd

式中：xd——期望位置。

控制器设计步骤如下[11]:

1)定义滑模函数为

(12)

其中，c>0，则

(13)

(14)

其中

则

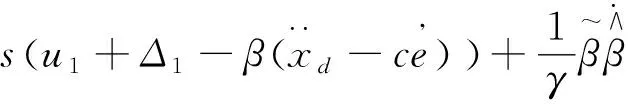
(15)

2)控制率设计

(16)

其中

ks>0，η>D

则

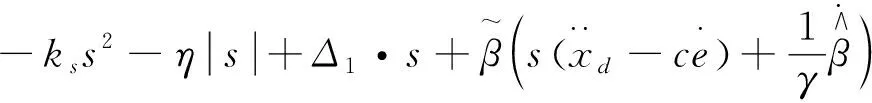
(17)

3)取自适应律为

(18)

则

(19)

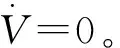
(20)

(21)

3 仿真结果及分析

文中介绍了四旋翼飞行器俯仰角的数值仿真结果。取J=1，Δ(1,2,3)取摩擦模型，表示为

控制输入采用自适应滑模控制率式(16)，自适应率采用式(18)，仿真结果分别如图2～图4所示。

图2 自适应滑模俯仰角与角速度的跟踪信号

图3 自适应滑模控制输入信号 图4 自适应滑模参数变化过程

如自适应率取式(20)，仿真结果分别如图5～图7所示。

图5 映射自适应滑模俯仰角与角速度的跟踪信号

图6 映射自适应滑模俯控制输入信号 图7 映射自适应滑模俯参数变化过程

从图2和图5可以看出，姿态角都能够在较短时间内跟踪上期望的值，映射自适应滑模相对于自适应滑模的角加速度较大，导致控制效果不理想。

从图3和图6可以看出，常规自适应滑模控制输入的瞬时值过大，映射自适应滑模控制输入信号在很小的范围内变化，可避免趋于饱和，达到很好的控制效果。

4 结 语

针对四旋翼飞行器参数的不确定性，分别采用自适应滑模与映射自适应滑模算法对姿态控制器进行设计，在MATLAB仿真软件平台上进行了仿真实验。仿真结果表明，两种自适应滑模算法都能使姿态角在较短时间内跟踪上期望值，而映射自适应滑模可限制参数β的自适应变化范围，防止控制输入信号u过大，以免系统执行器饱和。