压电粘滑驱动器研究现状与进展分析

程廷海, 高 琪, 李义康, 李恒禹, 何 猛, 卢晓晖

(1.长春工业大学 汽车工程研究院， 吉林 长春 130012;2.长春工业大学 机电工程学院， 吉林 长春 130012)

0 引 言

具有微纳米定位精度的压电驱动技术是精密光学系统、微/纳米制造、生物医疗工程、精密科学仪器等领域的支撑性技术之一。其中，基于粘滑驱动原理的压电驱动器因具有结构简单、精度高、行程大和无电磁干扰等特点得到了广泛关注[1-3]。压电粘滑驱动其实质上是利用压电元件的惯性驱动原理，实现动子的往复直线运动输出。简单概括为在非对称锯齿电压信号激励下，利用压电振子的不对称振动所造成的动、静摩擦力之间的差异，以达到控制被驱动物体产生微小位移的目的[4-6]。

文中将首先介绍压电粘滑驱动器的工作原理，然后从驱动器的新构型设计、激励波形优化设计、理论建模分析及控制方法研究等方面对其研究现状进行论述，分析当前研究主要存在的问题，介绍近年来相关研究工作的最新进展。

1 压电粘滑驱动器工作原理

典型的压电粘滑驱动原理与过程示意图如图1所示。

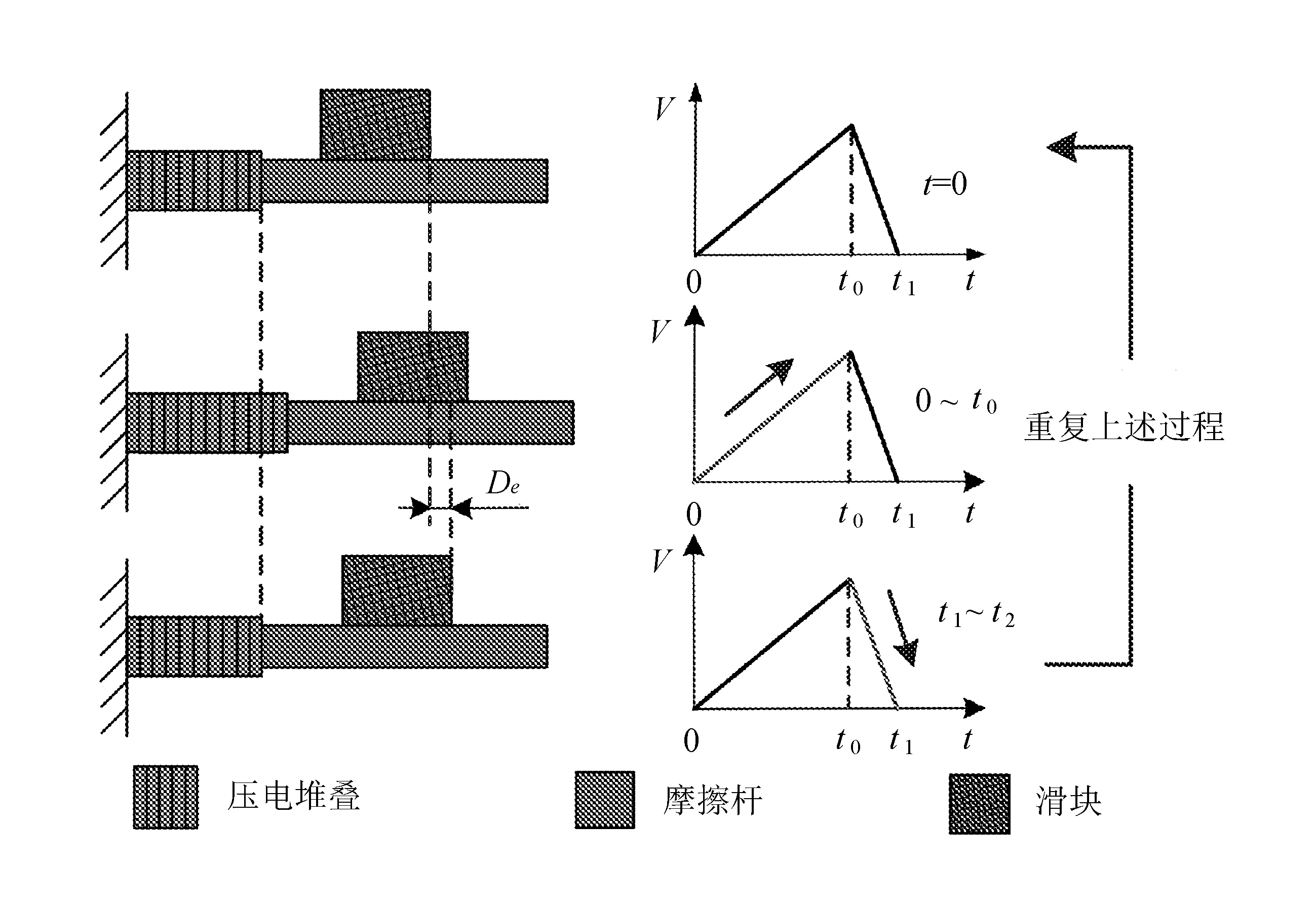
图1 压电粘滑驱动原理与过程示意图

压电粘滑驱动器在工作过程中主要采用非对称锯齿波对压电堆叠进行缓慢与快速交替激励，利用逆压电效应激发定子(图中定子由压电堆叠与摩擦杆构成)产生缓慢与快速交替的运动变形，使得定子与动子(图中动子为滑块)处于“粘”和“滑”两种运动状态，在摩擦力作用下实现机械运动输出[7]。

压电粘滑驱动器在一个运动周期内的工作过程可描述为以下几个阶段：

1)当t=0时刻，压电堆叠未得电，压电堆叠的伸长量为零，此时滑块与摩擦杆处于静止状态。

2)当t=t0-t1时段，压电堆叠在电信号激励下缓慢伸长，定子在静摩擦驱动力作用下“粘”住动子一起运动，向右产生一段微小的距离Ds。

3)在t=t1-t2时段，压电堆叠迅速收缩至初始长度，此时动子所受滑动摩擦阻力与其运动方向相反。因此，当惯性力不足时，动子将产生向左的回退位移Db。驱动器的有效输出步距De大小为Ds-Db。重复上述周期性激励，可实现驱动器宏观上的连续运动输出。

2 压电粘滑驱动器的研究现状

近年来，压电粘滑驱动器在新构型设计、激励波形优化设计、理论建模分析以及控制方法等几个方面得到了广泛研究，文中将围绕这几个方面着重进行论述。

2.1 驱动器新构型设计

从驱动器的新构型设计研究角度来讲，由于新构型设计灵活，国内外学者们开展大量研究工作。2004年，国内学者程光明等[8]采用双压电晶片振子为移动机构的驱动源，提出了一种新型二维压电驱动机构。该机构是通过控制机构驱动足产生的驱动力与接触面间的摩擦力共同作用实现机构的定向运动。此外，2006年研制了粘滑型实验装置样机，压电薄膜精密运动平台试验样机如图2所示。

图2 压电薄膜精密运动平台试验样机

图中，当驱动电压低于30 V 时，步距误差不超过0.5 μm，承载能力约为自重的7～8倍[9]。

2006年，加拿大学者Zhang等[10]利用粘滑驱动原理设计了一种多自由度压电粘滑驱动器，如图3所示。

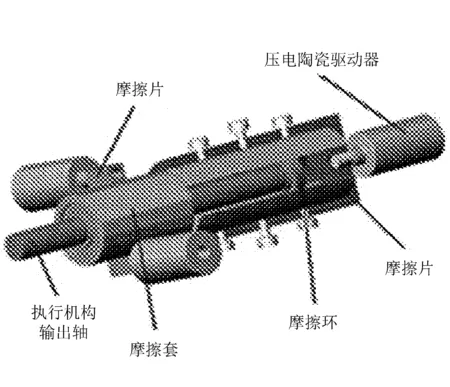
图3 二维压电粘滑驱动器结构示意图

该驱动器包括执行机构输出轴、摩擦套、摩擦环、摩擦片和压电陶瓷驱动器等部分。其中，该驱动器的直线运动可通过一个压电陶瓷驱动器实现，而旋转运动可通过两个压电陶瓷反方向伸缩带动输出轴旋转，并搭建驱动器的实验测试系统，进行了实验研究。实验结果表明，驱动器具有较好的输出性能。

2009年，国内学者冯志华等利用纤维扭转式驱动器研制了具有较高定位精度和运动分辨率的旋转式微型压电粘滑驱动器[11-12]，如图4所示。

该驱动器可实现较好的运动输出。在直线驱动器方面，利用一种基于简谐振动合成的共振型钳位机构设计了压电直线型驱动器[13-14]，通过调节机构尺寸来分别匹配共振频率比为1∶3∶5和1∶2。实验结果表明，该类驱动器可实现较好性能输出。

图4 纤维扭转式压电粘滑驱动器

2012年，日本学者Morita等[15]提出了一种共振型压电粘滑驱动器，该驱动器结构简单，并且利用的共振模式可实现高输出功率。

并于2013年利用压电堆叠设计了共振型杆式压电粘滑驱动器，当定子与动子间的预紧力为270 mN时，在1.6 V电压下，驱动器可获得的空载速度为40 mm/s，该压电驱动器具有较好的低电压特性，同时较好地抑制了驱动器的产热量[16]。

共振型压电粘滑驱动器如图5所示。

图5 共振型压电粘滑驱动器

2013年，立陶宛学者Mazeika等[17]利用压电双晶片作为驱动源设计了一种压电粘滑线性驱动装置，驱动装置样机的实物照片如图6所示。

在锯齿和脉冲信号激励下，驱动装置具有较好的输出特性。当脉冲信号的频率为153.37 Hz时，输出的平均速度最大。该驱动器的输出位移和速度主要取决于接触面间的滑动摩擦阻力，接触面间的滑动摩擦阻力越大，输出位移与速度越小。

图6 压电粘滑线性驱动装置

2013年，国内学者赵宏伟等[18]基于钳式结构寄生运动原理设计并研制一种旋转型压电粘滑驱动器，驱动器样机结构如图7所示。

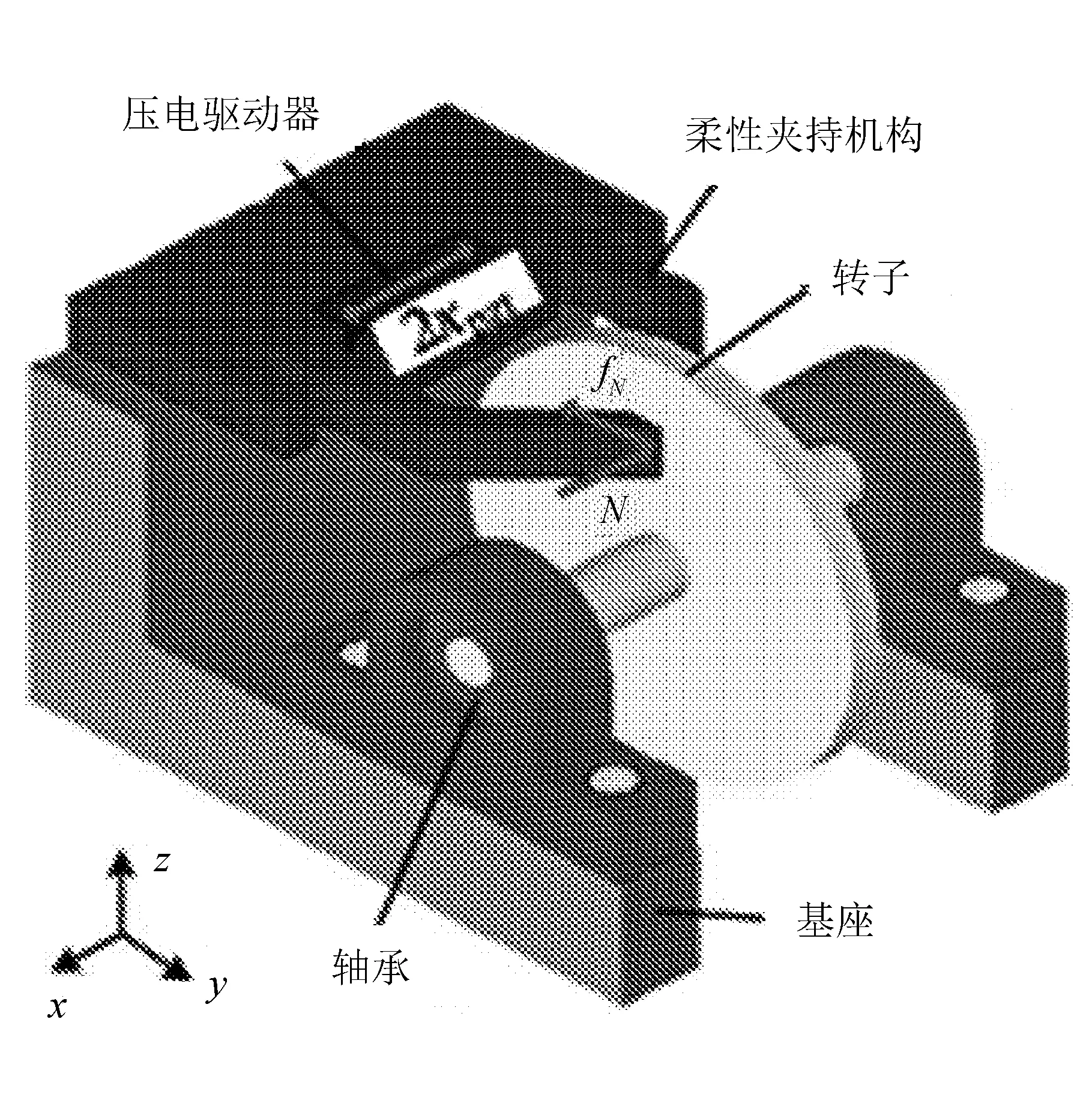
图7 旋转型压电粘滑驱动器

该压电驱动器的最小分辨率为0.7 μrad。基于寄生运动原理研制一种直线压电粘滑驱动器[9-21]。在先前研究工作的基础上，2015年，基于侧向运动原理研制一种压电粘滑驱动器[22]，该驱动器在实现大行程的同时兼具较高的分辨率。该驱动器的最大输出速度能够达到14.25 mm/s，最大输出力为3.43 N，最小步位移约为0.04 μm。此外，还研制了一种旋转型压电粘滑驱动器，该驱动器能够实现双伺服纳米定位台的宏-微复合定位[23]，其最大速度为32 000 μrad/s，旋转分辨率约为1.54 μrad。在2017年，又基于耦合运动设计并研制了新型驱动原理的压电粘滑驱动器，实验结果表明,驱动器可实现较理想的运动输出[24]。

2017年，国内学者荣伟斌等[25]研制一种新型旋转式压电粘滑驱动器，如图8所示。

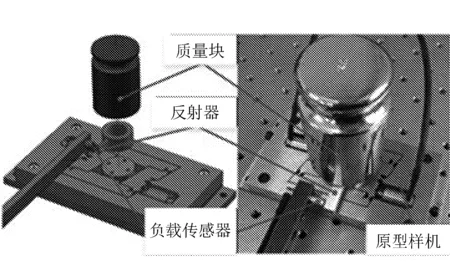
图8 新型旋转式压电粘滑驱动器

该驱动器基于压电堆叠和柔性铰链机构共同作用实现驱动，压电堆叠产生的微位移可通过柔性铰链机构进行放大，在保证较高分辨率的同时，实现较大的行程输出，柔性铰链机构致使定子与转子间处于静摩擦驱动力与滑动摩擦阻力交替变化状态，实现转子的运动输出。通过调节输入电压和频率，以实现不同的驱动器速度输出。驱动器的分辨率为0.75 μrad，最大负载能力为74 N。

2017年，国内学者范尊强等[26]研制了一种双堆叠共同驱动式直线压电粘滑驱动器，该装置主要由桥式柔性铰链机构和平行四边形柔性铰链机构复合而成，将两个压电堆叠的变形分别放大作用于滑块，压电堆叠B用于产生沿着导轨方向的驱动，压电堆叠A产生垂直于导轨方向的力，用于预紧力调节，如图9所示。

图9 双堆叠驱动式压电粘滑驱动器

实验结果表明，该驱动器可实现大行程直线运动，最小步长为0.29 μm，最大速度可达3.27 mm/s。

2.2 驱动器波形优化设计

从驱动器激励波形优化设计角度来讲，当前压电粘滑驱动器主要是利用非对称锯齿波的缓慢和快速交替通电来激发定、动子间产生“粘”与“滑”两种工作状态，通过分析该锯齿波电信号激励下驱动器的粘滑运动原理可知，在压电粘滑的快速变形驱动阶段，该锯齿波电信号的输入将会显著削弱其驱动器输出性能。并在此基础上，逐步发展出梯形波、摆线波以及指数波等激励波形。

2012年，国内学者陆轻铀等[27]研究了不同波形激励下压电粘滑驱动器的输出特性规律，如优化的锯齿波、梯形波和摆线波等。结果表明,在缓慢变形与快速变形交替的过渡阶段，通过对激励电信号施加适当的时间延迟，可抑制驱动器位移回退运动的产生，提升驱动器的有效步距，进而提升其速度和负载等输出性能。压电粘滑驱动器的典型激励波形电信号如图10所示。

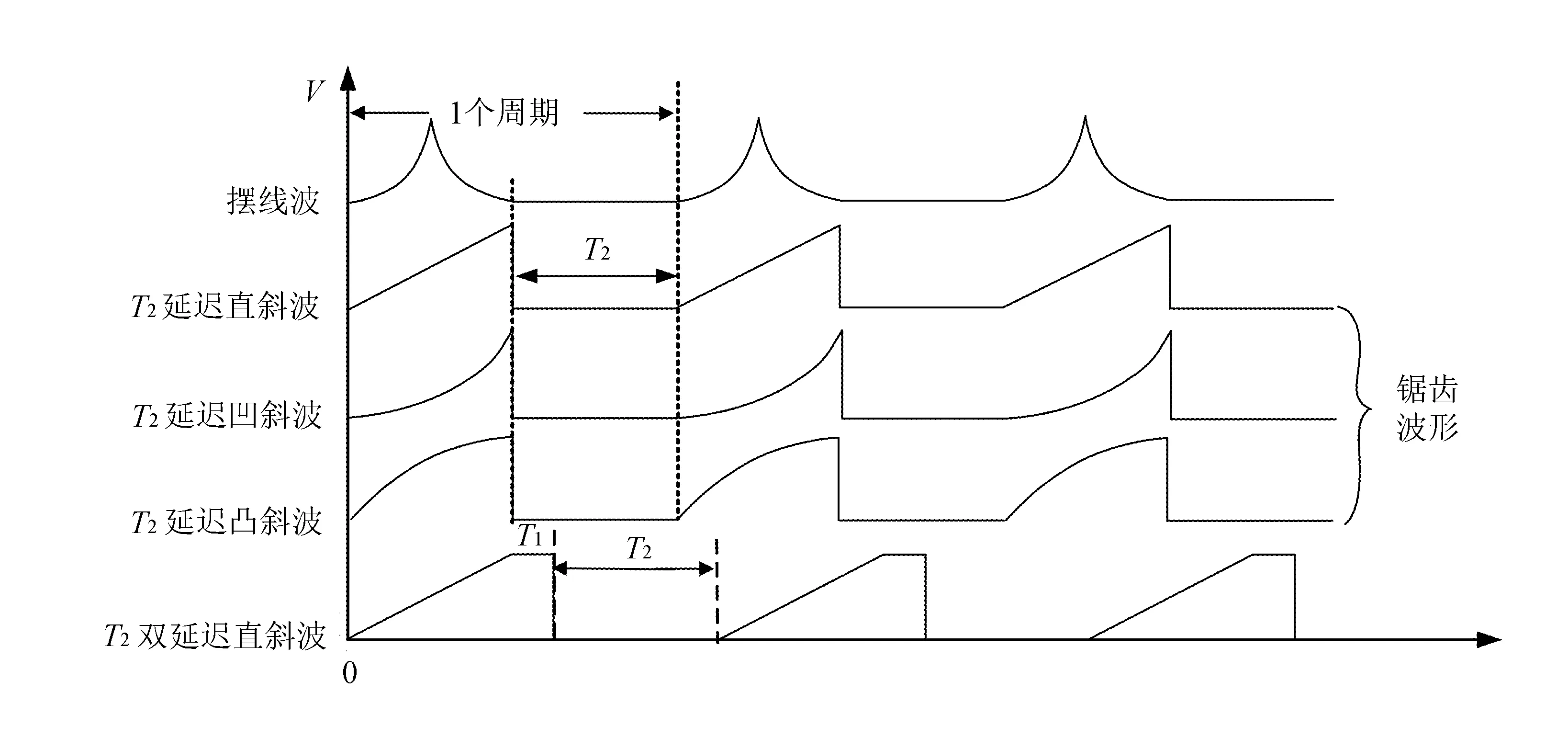
图10 压电粘滑驱动器的典型激励信号

2012年，捷克学者Neuman等[28]采用幂函数激励电信号对压电陶瓷剪切片进行激励，提升了压电粘滑驱动器的机械输出性能。除了捷克学者提出的幂函数电信号之外，当前压电粘滑驱动器采用的几种典型激励电信号波形如图11所示。

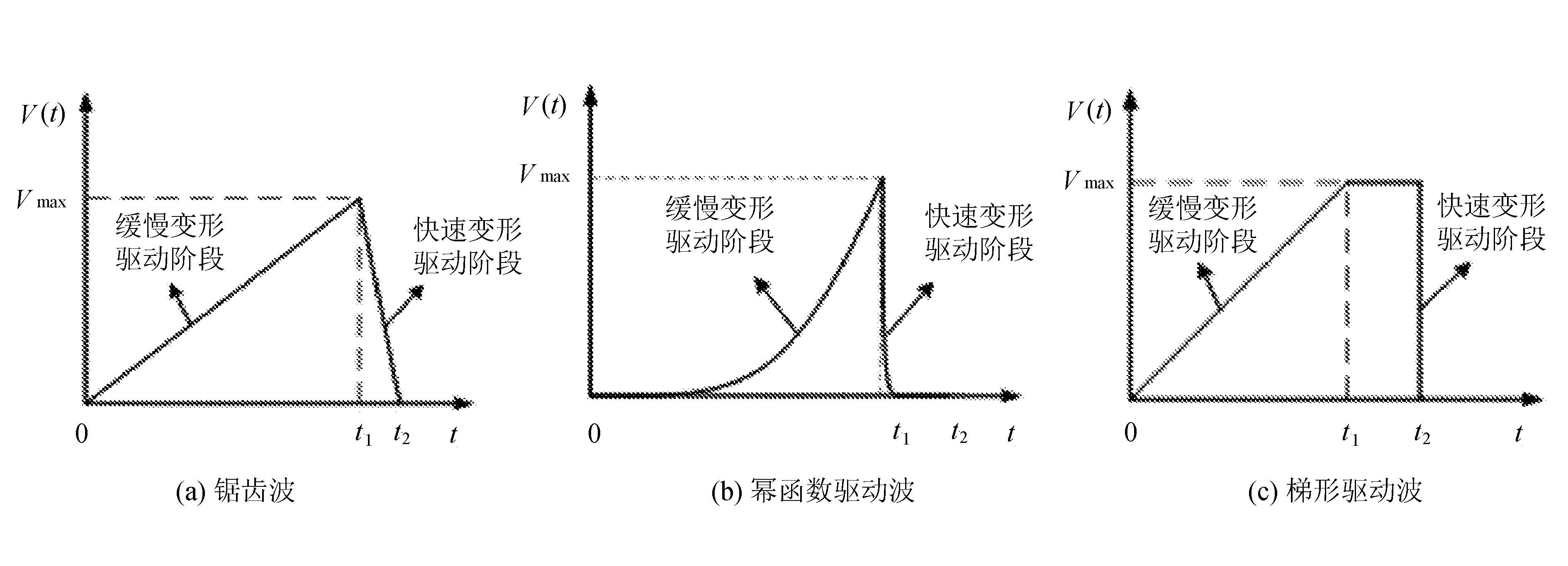
图11 当前压电粘滑驱动器采用的激励电信号

2.3 驱动器理论建模分析

由于压电粘滑驱动器主要依靠滑动摩擦阻力与静摩擦驱动力的相互转换致使定、动子间处于“粘”与“滑”两种运动状态，建立了粘滑理论等效模型，研究了其摩擦调控机理。2011年，德国学者Edeler等基于弹塑性理论建立粘滑驱动原理不同运动阶段等效运动状态模型和机械系统等效动力学模型。实验测试较好证明了该粘滑理论分析结果的正确性[29-30]。粘滑原理不同阶段等效模型如图12所示。

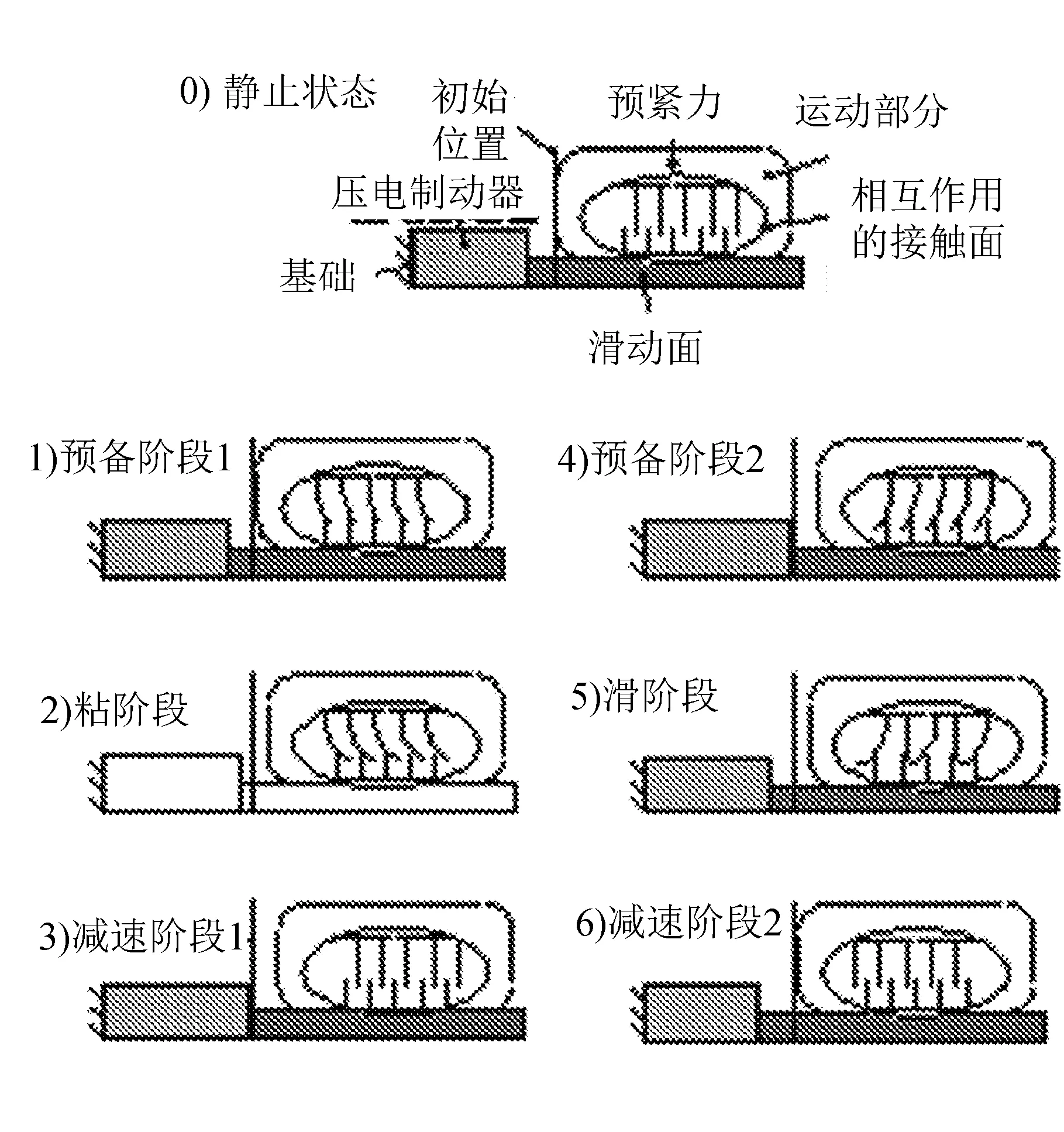
图12 粘滑原理不同阶段等效模型

机械系统的等效动力学模型如图13所示。

图13 机械系统等效动力学模型

2013年，德国学者Hunstig等建立了压电粘滑驱动器定、动子间摩擦力的动力学仿真模型，并搭建了驱动器的实验测试系统，通过数值模拟和实验研究方式对压电粘滑驱动器的摩擦特性进行了分析；随后又对压电粘滑驱动器缓慢与快速变形驱动阶段的运动状态进行研究，揭示了缓慢与快速变形驱动阶段输出特性的影响因素及其作用规律，指出在快速变形驱动阶段产生的滑动摩擦阻力是导致驱动器产生位移回退运动的主要原因[31-35]。压电粘滑驱动器定、动子间的受力分析如图14所示。

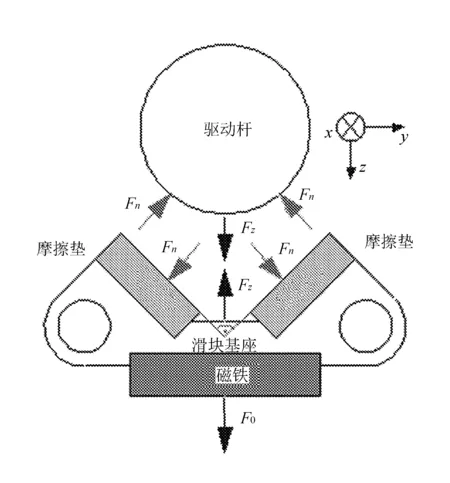
图14 定动子间受力分析示意图

接触面间的粘滑驱动等效力学模型如图15所示。

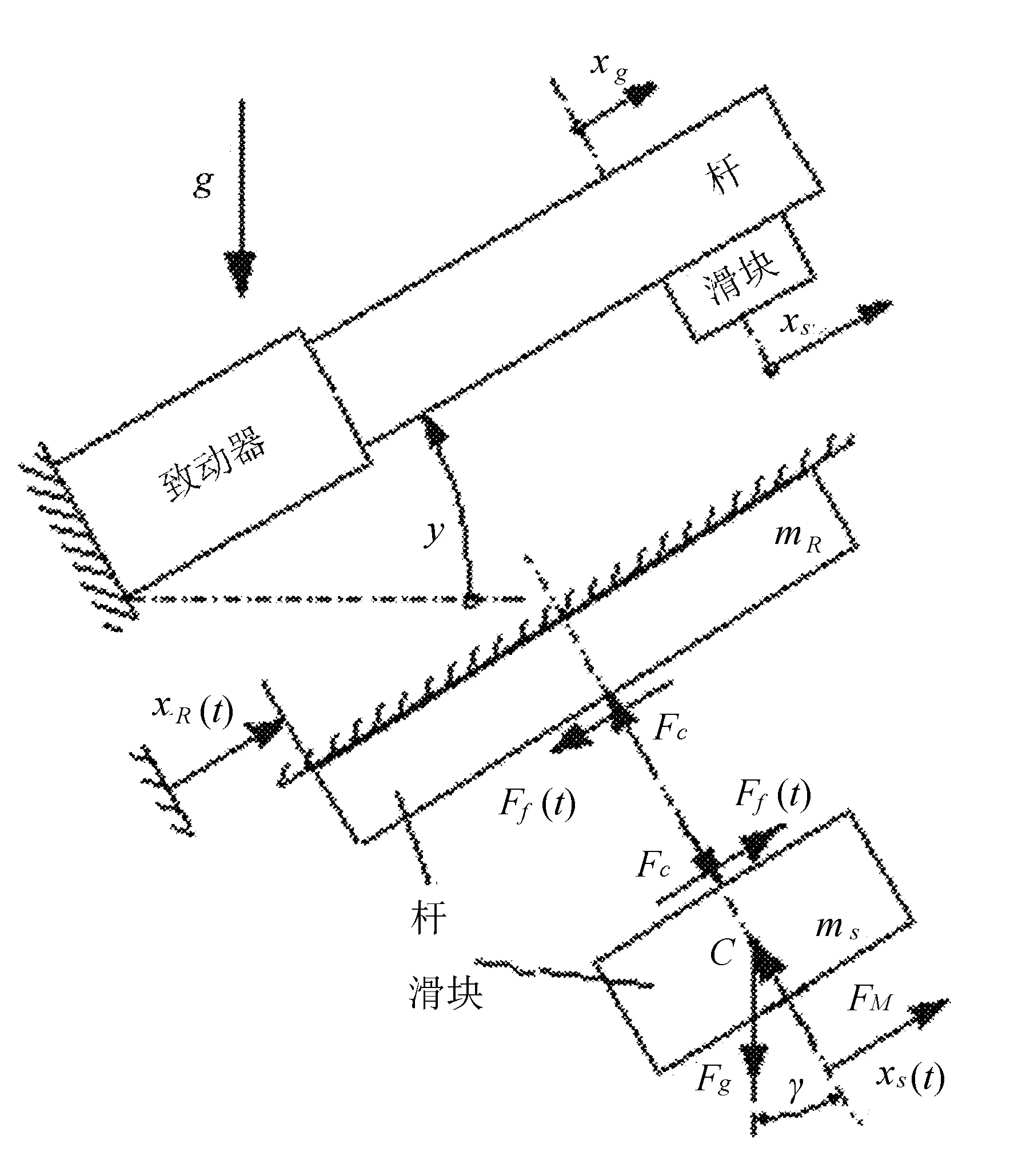
图15 粘滑驱动等效力学模型

2.4 驱动器控制方法研究

从驱动器控制方法研究角度来讲，为保证压电粘滑驱动器有着良好的运动性能，基于PID反馈控制的闭环系统得到广泛应用；1998年，Breguet等[36]采用数字频率比例控制器，将位移误差转换并反馈给时间信号，使频率与误差成比例，计数器输出信号根据误差增减，当到达期望位置时，频率趋向于零。此外，在压电粘滑驱动器控制系统中，通常会将前馈控制和反馈控制结合使用，以达到更好的控制精度[37-39]。

2008年，Rakotondrabe等[40]提出电压/频率(U/f)比例控制方法，通过电压饱和函数和频率饱和函数来避免产生过电压以及使驱动系统在频率的线性范围内工作，选择控制方式，电压U和频率f与误差ε的比例系数；KU和Kf同经典比例控制相同，通过仿真和实验得出控制器稳定性较高，特别是在频率控制下系统稳定时误差趋于零，精度很高。

2018年，中科院研究所Cheng等[41]提出一种可实现压电粘滑驱动装置精密控制的智能神经网络控制方法。首先，通过建立神经网络模型对驱动装置末端执行器与被驱动物体间的相对运动进行捕获，实现整个驱动过程的精密控制。然后，开发了一种基于神经网络控制算法的逆向模型，在末端执行器预先标定的前提下，在线计算压电执行器的理想位置。最后，采用一种基于动态线性化神经网络的模型预测控制方法，有效地处理驱动器控制过程中存在的迟滞和非线性等特性，实现了压电执行器的位移控制，最终获取了一种高精度的控制器。研制了压电粘滑驱动装置的原型样机，通过实验验证了提出新方法的可行性。

综上所述，上述研究学者已经在压电粘滑驱动器新构型设计、波形优化设计、理论建模分析及控制方法研究等方面取得了较好的研究成果，并且得出驱动器定、动子间的摩擦力是影响驱动器输出性能的关键因素。

3 压电粘滑驱动器的研究进展

压电粘滑驱动器工作过程受力分析和典型位移输出曲线如图16所示。

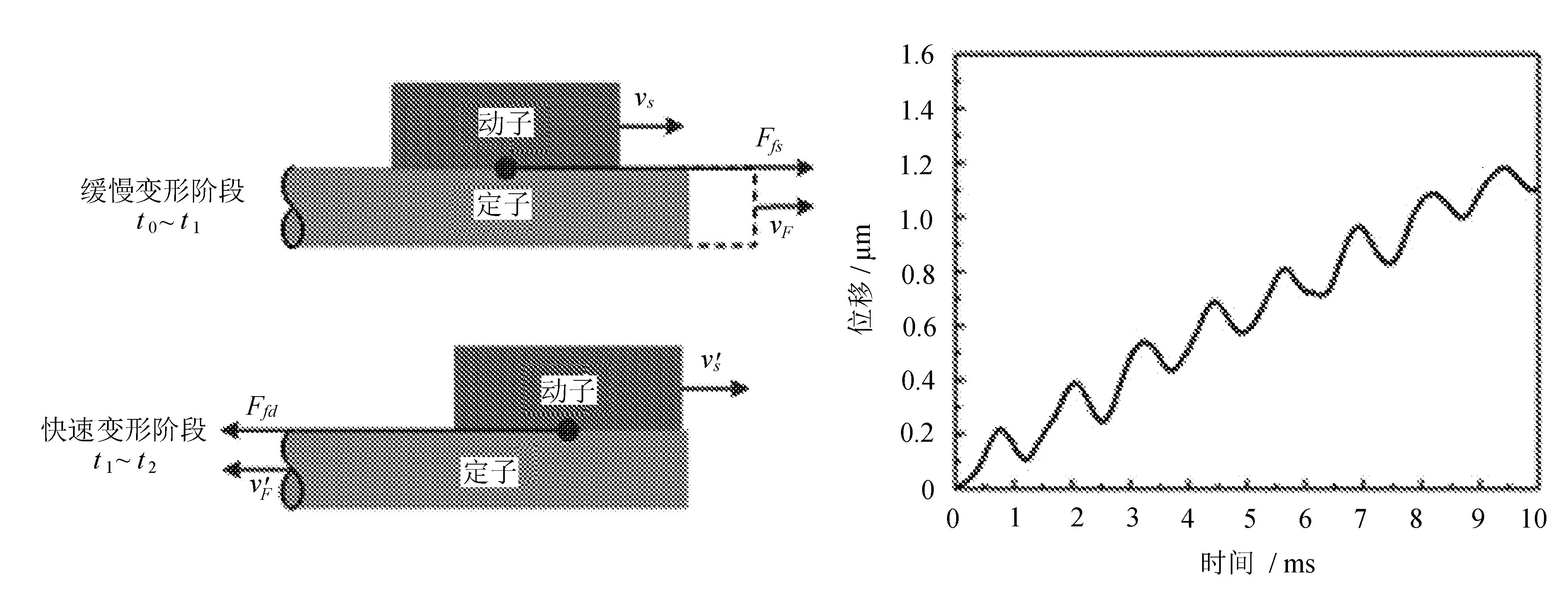
图16 压电粘滑驱动器工作过程受力分析和典型位移输出曲线

由图16可以看出，在缓慢变形驱动阶段，定、动子间的静摩擦力为驱动力，此阶段增大静摩擦驱动力将会提出驱动器输出性能；在快速变形驱动阶段，定、动子间的滑动摩擦力为阻力，此阶段减小动摩擦阻力将会改善驱动器输出性能。

在压电粘滑驱动过程中，增大缓慢变形阶段的静摩擦驱动力，同时减小快速变形驱动阶段的滑动摩擦力是提升驱动器输出性能的关键。基于此，具有摩擦调控功能的压电粘滑驱动器研究成为当前研究热点。针对压电粘滑驱动器摩擦力调控困难的问题，研究学者主要从驱动器的新材料制备、驱动方法和新构型设计等方面对压电粘滑驱动器进行研究。

3.1 定/动子接触面新材料制备方面

2012年，加拿大学者Chen等[42]尝试采用化学微加工方式对定子与动子接触表面进行处理，研制出一种具有各向异性摩擦接触表面的压电粘滑驱动器。其研制的压电粘滑驱动器样机与输出位移测试结果如图17所示。

从位移曲线可以看出，由于驱动器定、动子接触面间采用了具有各向异性材料特性的摩擦接触表面，改变了驱动过程中定子与动子接触面间的摩擦状态，在单方向驱动时(论文表述为正向)显著提升了驱动器的输出性能，减小了位移回退。

3.2 压电粘滑复合驱动方法

2016年，针对当前压电粘滑驱动器普遍存在的位移回退运动问题，国内学者程廷海等提出了基于超声减摩效应的压电粘滑复合驱动方法[43-46]，复合驱动方法的工作原理和输出位移特性测试结果如图18所示。

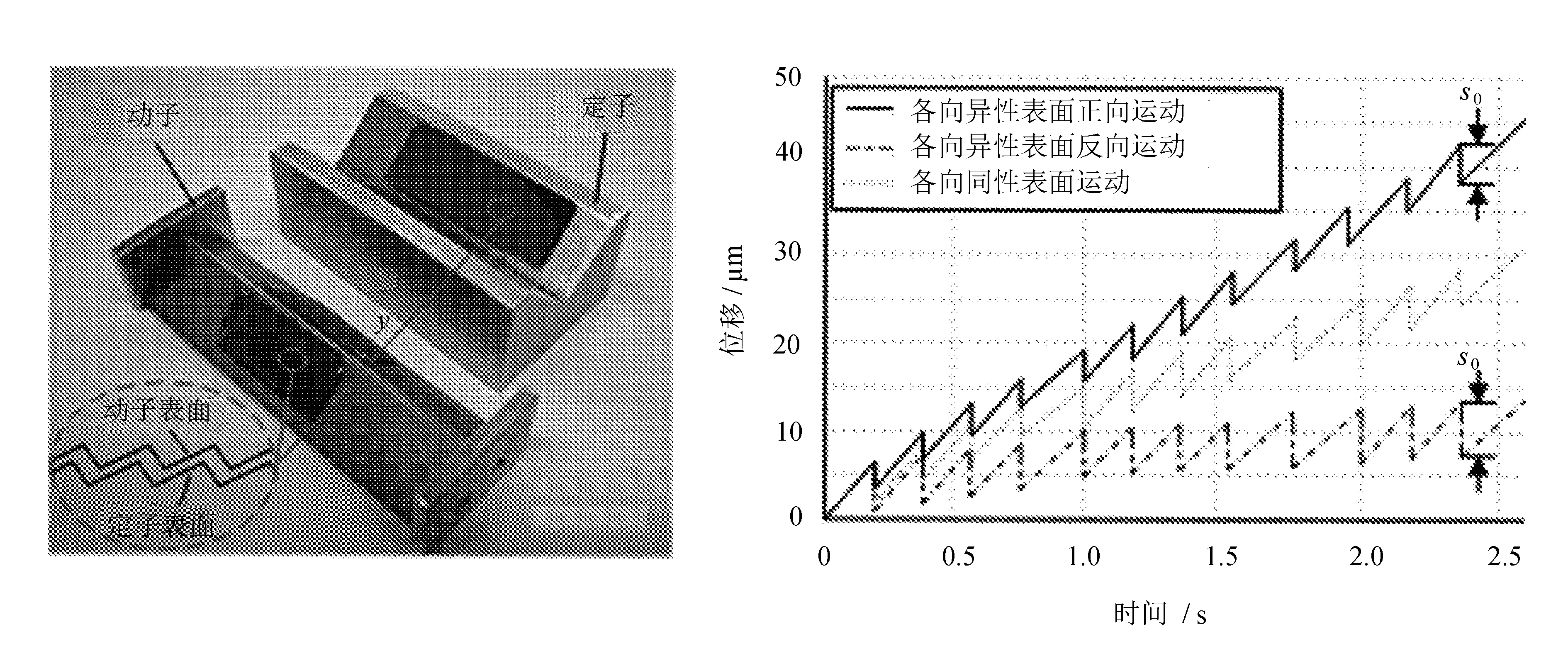
图17 文献[42]研制的压电粘滑驱动器样机与输出位移测试结果

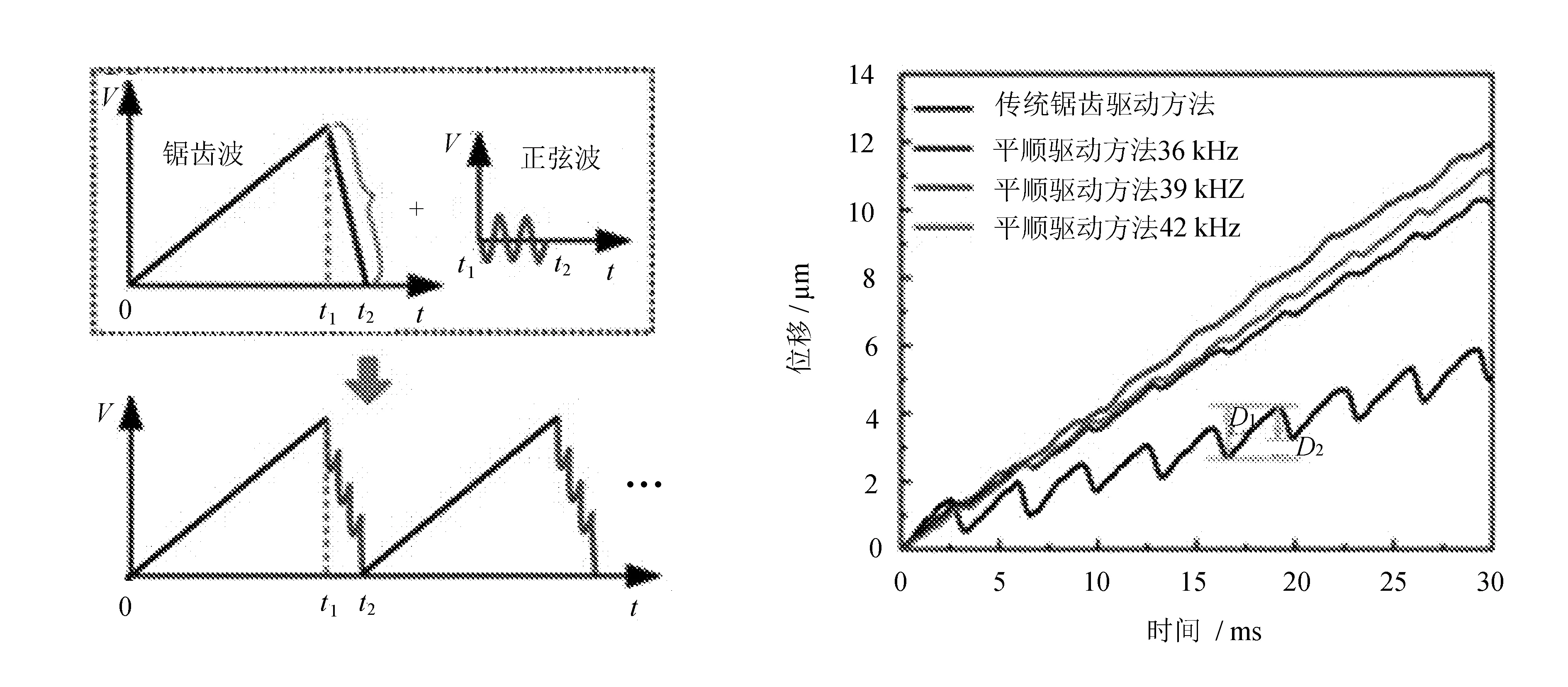
图18 压电粘滑复合驱动方法工作原理与输出位移测试结果

该新方法可通过复合驱动波形实现，具体包括锯齿波和正弦波，通过将微幅高频正弦波耦合施加到锯齿波的快速变形驱动阶段，激发定子在快速变形驱动阶段处于微幅高频振动状态，基于超声减摩效应降低了驱动器定子和动子间的滑动摩擦阻力，实现了驱动过程中摩擦力的综合调控，显著抑制了驱动器的位移回退，提升了驱动器的速度和负载特性。实验结果表明，相比于传统锯齿驱动方法，提出的复合驱动新方法可将驱动器的位移回退降低至20%以下。

3.3 结构非对称式压电粘滑驱动器

2017年，国内学者程廷海等[47]针对已有压电粘滑驱动器较难实现对缓慢与快速变形驱动阶段摩擦力进行综合调控，限制其输出性能这一共性问题，提出一种结构非对称式压电粘滑驱动器。研制的压电粘滑驱动器样机与输出位移测试结果如图19所示。

通过将非对称柔性铰链机构引入定子结构设计，使得定子轴向刚度分布不均，激发定子驱动足产生侧向位移实现驱动，并调整定子与动子间的轴向接触正压力，实现对缓慢与快速变形驱动阶段摩擦力的综合调控，提升压电粘滑驱动器的整机输出力与速度能力。实验结果表明，结构非对称式压电粘滑驱动器的最佳工作频率为500 Hz，最大输出速度可达5.96 mm/s，开环条件下最小位移分辨率为50 nm，最大负载为3 N，样机的最大效率为0.90%。

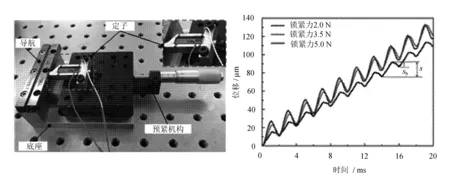
图19 压电粘滑驱动器样机与输出位移测试结果

4 结 语

介绍了压电粘滑驱动器的工作原理，总结了当前压电粘滑驱动器的国内外研究现状，得出当前研究工作主要集中在驱动器的新构型设计、激励波形优化设计、建模理论分析和控制方法研究等方面。针对当前压电粘滑驱动器存在的摩擦力综合调控困难等问题，从驱动器的新材料制备、驱动方法设计和新构型设计等方面论述了压电粘滑驱动器的最新研究进展。