平方反比有心力作用下的二体系统的一套初等教案

周国全

(武汉大学物理科学与技术学院,湖北 武汉 430072)

自然界中典型的两种引力——万有引力与静电引力, 都属于平方反比有心力系统[1-3], 除了遵守通常的有心力系统所满足的机械能与角动量守恒定律、比耐微分方程与位力(Viary) 定理之外[4-7], 还满足其独有的高斯定理和LRL(Laplace-Runge-Lenz的缩略)守恒矢量[6-12]。

科学史告诉我们，开普勒先后发现太阳系的3个行星定律，牛顿由此推导出万有引力公式，但有关太阳系行星的公转运动，教材、文献一般采用的求解是基于牛顿的万有引力理论及其经典力学的比耐微分方程，或者运用其他高等方法加以解决[4-7，13]，文献[8-12]采用隆格-楞次守恒矢量方法，它是一种优雅而精致的初等方法，仅需学生理解并使用三矢量混合积的轮换恒等式，以及四矢量混合积的拉格朗日公式等数学知识。本文面向大学理工科低年级大学生以及中学物理竞赛的师生，总结了自己长期从事奥林匹克物理竞赛的培训经验，并未遵循天体运动规律的科学史的发现轨迹，而从教学的方便性需要和理论的逻辑连贯性的目的出发，展示了有关这一问题的另一套初等解决方案，即运用牛顿的万有引力公式，以及有心力系统的机械能E的守恒性质，并仅仅基于行星质心绕太阳质心的周期性椭圆运动规律(开普勒第一定律)和公转角动量L的守恒性质(等价于开普勒第二定律)，力避求解复杂的微分方程，突出利用一元二次方程的韦达定理等初等数学技巧，给出了在平方反比有心力作用下，开普勒系统之轨道问题的一套初等教案。具体而言，本文推导了其轨道方程之诸参数、能量公式、特殊点的运动参数(速率与曲率半径)；再结合万有引力公式，用巧妙的初等方法逆向推导出开普勒三定律；进而通过引入质心系中二体开普勒系统的等效的单体描述，给出了前述理论对二体情形的修正和统一的表达形式。

1 有心力系统的一般性质

自然界中存在着一类特殊力系——有心力系统，作用在质量为m的质点上，它可表达为

F(r)=f(r)r/r∥r

(1)

其中，r是质量为m的质点绕质量为M的不动的质点作开普勒运动的相对位置矢量。平方反比有心力系统具有一般有心力系统所共有的如下性质：

(1) 角动量守恒，即满足开普勒第二定律。开普勒观察太阳系行星系统所得到的开普勒第二定律，即太阳质心(力心)与运动行星的质心连线在相同时间内扫过的面积是不变的、守恒的，亦即掠面速度守恒。它体现的不仅是平方反比有心力系统所特有的性质，更是一般有心力系统普遍满足的角动量守恒这一共性规律。事实上，由于有心力关于力心的力矩为零r×F(r)=0，自然导致运动质点关于力心的角动量L=r×p=r×m守恒，称为角动量守恒定律

dL/dt=0

(2)

而掠面速度

(3)

即单位质量的角动量h=L/m之半。这是因为|r×dr|/2正是质点的位置矢量r在dt时间内扫过的无穷小三角形(扇形)的面积。

(2) 保守力特性与机械能守恒。

运用文献[14]的一个有关微分矢量的定理及其推论, 从F(r)∥r可得F(r)·dr=F(r)dr，进而可证明一切有心力系统均为保守力系，满足机械能守恒定律

mv2/2+V(r)=E

(4)

其中E，V(r)分别为有心力场中运动质点的机械能与势能。

(3) 质点运动轨迹的平面曲线特性，即有心力作用下质点必作平面轨道运动。

在相对力心(不动质点M)的惯性系，并以力心为原点的空间直角坐标系O-xyz中，运动质点(m)的位置矢量r(x,y,z)与其守恒的角动量常矢量L(a,b,c)之间满足正交关系L·r=0，这是因为L=r×m⊥r，于是

L·r=ax+by+cz=0

(5)

这个平面方程说明运动质点在有心力作用下必作平面轨道运动。容易验证，力心(0,0,0)就在此轨道平面上, 这正好符合开普勒第一定律的表述：“太阳是这些椭圆轨道的焦点”,当然必须在其轨道平面上。

(4) 有心力作用下质点的平面极坐标(r(t),θ(t))满足运动微分方程组

(5) 位力定理(Virial theorem)是一个带有统计平均性质的定理。无论宏观或微观领域，也无论经典或量子情形，它都可以表示为〈T〉=-〈F·r〉/2。其中符号〈…〉表示对时间的平均。T是总动能；F和r分别是作用于质点上的力和质点的位矢。克劳修斯(Clausious)把上式右边叫作均位力，所以上式也称位力定理。当作用力具有势能V时，F=-V,位力定理可表达为

〈T〉=-〈V·r〉/2

(8)

特别是对于平方反比有心力，位力定理可表达为

E=-〈T〉=〈V〉/2

(9)

(6) 在极坐标系中，运动质点的轨道r=r(θ)满足比耐微分方程

mh2u2d2u/dθ2+u=-f1/u

(10)

其中u(θ)=1/r(θ)的第4、5、6条性质式(6)～式(10)是本文力避使用的高等方法。

2 平方反比有心力作用下质点的二次轨道问题的初等方法

2.1 平方反比有心力系统的一般性质

对于平方反比有心力系统，其势能的表达式V(r)=k/r(设定无穷远处势能为零)，当其中的常系数k=-GMm时，适用于万有引力系统, 而当常系数k=Qq/4πε0时, 适用于质量为M,电量为Q的点电荷与质量为m, 电量为q的点电荷之间在M≫m条件下的静电场库仑引力系统。其中势能V(r)与相应的平方反比引力场的引力F的关系为

F(r)=f(r)r/r=kr/r3=-(k/r)=-V(r)

(11)

因此

E=Ek+V(r)=mv2/2+k/r； dE/dt=0

(12)

因而根据牛顿第二定律,质点(m)的动力学方程可表达为

dP/dt=-V(r)=kr/r3

(13)

其中P=m和分别为质点(m)相对于不动的质点(M)的动量和速度。

2.2 平方反比有心力作用下的椭圆轨道问题的初等方法

先讨论单体质点绕不动的力心F2作椭圆轨道运动的理想情形(相当于力心处质点因其质量远大于单体质量而不动的情形)。对于中学生，我们避开动力学原因而直接承认开普勒第一定律，(8大行星各自独立地在一个以太阳为焦点的椭圆轨道上作周期运动)；并接受有心力的前述两条性质——机械能守恒、角动量守恒(进而满足开普勒第二定律)；可将质量为m的质点的机械能E与其绕力心的角动量L(及其大小L)作为初始条件。如图1所示, 在以椭圆中心为坐标原点的直角坐标系中，质点的轨迹方程为

x2/a2+y2/b2=1

(14)

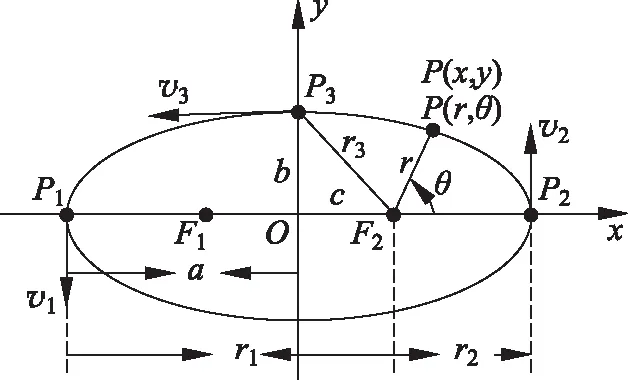
图1 平方反比有心力作用下的二次曲线轨道(以椭圆为例)

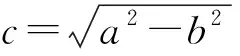
r(θ)≡r0/(1+ecosθ)

(15)

其中，r0为半正焦弦长；e≡c/a为椭圆的偏心率。设r1，r2分别为右侧焦点到左右两拱点的距离(即到远日点及近日点的距离)，它们之间的几何关系为

因此有

(18)

而偏心率

(19)

在拱点，r⊥，且

从式(20)、式(21)中消除v，可得拱点的位矢长r，它们是如下一元二次方程的解

2Er2-2kr-mh2=0

(22)

韦达定理给出其两根之如下关系

由式(16)及式(23)、式(24)立即可得椭圆轨道的能量公式

E=k/2a=-mh2/2b2=-L2/2mb2

(25)

再从式(20)、式(21)中消除r，可得拱点的速率v，它们是如下一元二次方程的解

v2+2k/mhv-2E/m=0

(26)

韦达定理给出其两根之如下关系

将式(23)、式(24)代入

(29)

质点的运动在其机械能E<0的情形，0≤e<1，属于椭圆运动；在其E=0的情形，由式(22)知轨道只有一个拱点，即近日点，偏心率e=1，属于抛物线运动；在其机械能E>0的情形，e>1，属于双曲线运动。

对于椭圆轨道情形，由式(23)、式(25)，可得其诸轨道参数如下，半长轴为

a=(r1+r2)/2=k/2E

(30)

焦距之半为

(31)

半短轴为

(32)

半正焦弦长(对于e<1的椭圆情形)为

(33)

其中，守恒量E、L由系统初值或任意时刻/位置的瞬时值给定。另外，相应于圆轨道情形，一元二次方程式(22)必有等根，其判别式Δ=4k2+8Emh2=0；或在式(29)中令偏心率e=0，可得如下圆轨道的能量公式

(34)

2.3 第三点的速率3的计算

第三点P3即轨道与y轴的交点，质点在点P3的速率有两种推导法

方法一：能量法, 由r3=a及机械能守恒，有

可得如下比例关系及v3的表达式

因而可求得v3之值

(35a)

以及一个意外的比例中项关系式(由式(28)可得)

(35b)

方法二：角动量守恒法。在第三点及第一、二点处应用角动量守恒定律

r3×m3=r1×m1=r2×m2

其大小亦为守恒量，即

注意到α3=(r3,3)，亦即r3与x轴反方向之夹角；在图(1)的直角三角形中sinα3=b/a，结合r1r2=b2，代入上式化简，也得到同样的比例中项关系式v3=再由式(28)进而可得即式(35a)。

2.4 轨道曲线3个特殊点P1、P2、P3的曲率半径

首先计算轨道在第三点P3处的曲率半径。由r3=a及如下运动方程

(36)

和图1中的直角三角形的边角关系sinα3=b/a，可得

ρ3=a2/b

(37)

又由拱点处的法向动力学方程

(38)

将以上二式相乘可得

m2(v1v2)2/ρ1ρ2=k2/(r1r2)2

又根据椭圆轨道的对称性ρ1=ρ2，因此由上式及式(24)、式(28)可得

ρ1=ρ2=b2/a

(39)

再由式(37)、式(39)可得ρ1ρ3=ab，于是椭圆面积S=πab=πρ1ρ3,即拱点处与第三点处的曲率圆面积的比例中项。

2.5 开普勒第三定律的证明

对于束缚态情形的封闭的周期性椭圆轨道，k<0时，还有一条著名的开普勒第三定律。虽然历史上它是由开普勒发现的一条独立的定律，但我们结合开普勒第一、第二定律和轨道的特征，运用牛顿万有引力理论，也可给出开普勒第三定律的初等证明。根据开普勒第二定律，对拱点处运用式(3)、式(20)，可得

(40)

将椭圆面积公式S=πab及韦达定理的表达式(24)、式(28)代入上式可得

(41)

整理即得

a3/T2=-k/4π2m，或T2/a3=4π2/(-k/m)

(42)

对于万有引力系统，上式中-k/m=GM称为太阳(对于太阳-行星运动)或地球(对于地球-卫星系统)的高斯常数。

3 对二体开普勒运动系统的修正

3.1 二体问题的质心系与等效的单体描述

仿照文献[10]的方法, 引入质心C和质心系的概念，即可将以上理论推广应用于二体问题；它既能描述质量任意的二体开普勒运动，又能同时适用于平方反比有心力系统。我们仍然以平方反比有心力作用下的椭圆轨道运动为例，讨论开普勒二体系统作各类二次曲线轨道运动的判据, 以及开普勒二体系统在质心系中作相对束缚态椭圆轨道运动的能量公式。

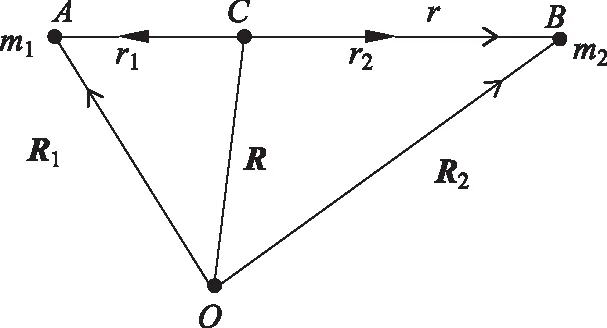
图2 实验室系中二体系统的运动描述

E=Ek+V(r)=μv2/2+k/r=P2/2μ+k/r

(43)

相对运动的动力学方程为(本文不直接运用)

μd2r/dt2=dP/dt=F(r)=kr/r3=-V(r)

(44)

由于质心系中，二体系统不受外力及外力矩作用,因此质心系中二体总角动量L=r×μ=r×P也是守恒的。最终我们将二体问题成功地转化为在质心系中折合质量为μ的单体的轨道问题。

3.2 二体相对运动轨道曲线的平面极坐标方程及分类判据，能量公式

基于以上等效的单体描述，可直接援引前文结论。在平方反比有心力作用下，二体运动的相对位置(r,θ)所满足的极坐标方程仍如式(15)，其偏心率e与半正焦弦长r0在k<0时可分类表达。对于万有引力系统二体轨道运动的高斯常数修正为GM=G(m1+m2)。

而对于异号点电荷之间的静电吸引力二体系统(k<0):

根据式(45)、式(47), 可得二体质心系中相对运动的轨道曲线的判据。

当总能量E<0，e<1，此时质点处于束缚态，其二体相对轨道为椭圆二次曲线; 尤其当E=-μk2/2L2时，e=0, 轨道为圆形; 当E=0时,e=1，轨道为抛物线; 当E>0时, 轨道为双曲线，又分为两种情形：当k=Qq/4πε0<0,总能量E>0时，即在异号电荷平方反比吸引力情形，由式(47)可知，e>1，相应的二体相对轨道为焦点(质心)在内的双曲线；而当k=Qq/4πε0>0,总能量E>0时，即在同号电荷平方反比排斥力情形，计算可知，e>1，相应的二体相对轨道为焦点(质心)在外的双曲线，极坐标方程为：

r(θ)≡r0/(-1+ecosθ)

(49)

这是只有一个拱点(近日点)，且焦点在外的散射型双曲线轨道，其初等方法，作者拟另文专述。最后，二体各自相对质心的轨道二次曲线分别为[10]

它们的轨道半正焦弦长分别变为μr0/m1及μr0/m2。而在平方反比有心吸引力作用下，二体Kepler系统的束缚态椭圆轨道的能量公式

E=k/2a

(52)

4 结语

基于有心力系统的机械能E的守恒性质与开普勒第一、二定律，本文给出了开普勒二体问题的一套初等的教学方案; 具体讨论了运动质点在平方反比有心力作用下的束缚态椭圆轨道问题，推导了其特征轨道参数、能量公式、轨道拱点等若干特殊点相对于力心的距离、速率与曲率半径；并可推广延伸到其他二次曲线(如抛物或双曲线)轨道问题，给出不同轨道类型的判据；这套解决问题的初等方法，为从事普通物理与理论力学教学，以及参加物理竞赛或自主招生的师生们提供了一个参考教案。