对膜簧片型汽笛频率影响因素的研究
冯舰锐 陈 聪 吴秀文 董爱国
(中国地质大学(北京),北京 100083)
汽笛是一种气动装置,旨在产生一种非常大的声音,起到警示的作用。它通常由一个产生压缩空气的源组成,通过把空气压入簧片或膜,再进入一个喷管,空气气流使簧片或薄膜振动,从而产生声波[1]。
手按式汽笛由于音量大而且携带方便,也常被用来作为运动竞赛或集会游行的造势器材。使用高压瓶或压缩机的空气喇叭音量更大,一般作为铁路机车,货车的安全警示装置[2]。但是,目前的汽笛发声部位主要由硬质金属簧片组成[3],且出于本质安全的需要,其频率集中在较高的范围,音色不够友善。在其他应用中,例如机车鸣笛噪声,在距轨道5m处,其声压级达到120dB之高。鸣笛声的频率成分主要在500~2000Hz的范围内,它恰好与人的语言频率相重,因此对人具有强烈的干扰性和烦躁影响[4],并且该噪声对人体最直接的危害是对听觉器官的损害。基于该问题,拓宽汽笛的声音频域范围具有重要实际应用价值。
膜簧片汽笛发声主要是由薄膜的一阶振动与空气柱内的空气振动发声引起,目前,国内外的研究主要集中在簧片的振动[5,6]与声音的激发[7],而综合考虑薄膜与空气柱同时振动对声音频率影响的理论与实验研究鲜见报道。在本研究中,汽笛内簧片由通常的硬质簧片改为软质橡胶膜,减少金属制品损耗的同时,拓宽汽笛所能达到的频域范围。该项改进对提高汽笛的性能、寿命和可靠性等有重要作用。
1 振动模型
1.1 薄膜振动模型
在声学上,圆形薄膜上一点自由振动的动力学方程为[8]
(1)
其中,z(m)是薄膜上一点离开平衡位置的垂直薄膜面方向的位移;r(m)是薄膜上一点到圆心的距离;σ(kg/m2)是薄膜的面密度;T(N/m)为薄膜的张力。方程(1)的解为零阶贝塞尔函数
(2)
根据膜边界振动位移为零,即zRcon,t=0,代入公式(2),得到
(3)
由公式(3)的第一个正根得到
(4)
其中,x01为零阶柱贝塞尔函数J0x的第一个正根;Rcon(m)是薄膜的半径或共振腔的半径。
当插入的管子贴靠在薄膜的正中间时,圆形薄膜上某点的振动动力学方程为
(5)
其中,z,r和T同上;σc(kg/m2)是薄膜等效面密度;p(Pa)为腔体内压强;p0(Pa)为标准大气压。由于空气造成的附加质量mα在薄膜上均匀分布,为方便求解,定义σc满足如下公式[9,10]
πR2σ+mα=πR2σc
(6)
由于腔体内压强受充气速率、薄膜性质等因素影响,并且与上一时刻的气体状态亦有关系,所以无法精确给出压强对于时间的函数关系。
由于薄膜凸起的体积相对整个汽笛体积极小,故可忽略管内气体体积的变化。由质量守恒定律和理想气体状态方程,可得汽笛腔内气体质量对时间t的微分等于进出管子内部的气体质量流速变化
(7)
其中,Qin(kg/s)是进气质量流速;Qout(kg/s)是出气质量流速;mintube(kg)是在管子内的气体质量。
此外,出气质量流速与流速的关系如下式
Qout=ρSinc
(8)
其中,ρ(g/cm3)是气体密度;Sin(m2)是气体流动截面的截面积;c(m/s)是气体速率。
一般情况下,由于频率为每秒几十至几百赫兹,即空气的一个振动周期时间很短,因此进气过程可视为绝热流动。式(9)是将气体的密度与温度和压强联系起来的物态方程
ρ=MpT-1R-1
(9)
其中,M(g/mol)为空气摩尔质量;R(8.314J/(K·mol))是理想气体常数;T(K)是汽笛内空气的温度。式(10)是绝热条件下的喷管流速公式[11]
(10)
其中,比热容比γ=Cp/Cv;p0(Pa)为标准大气压。
由式(7),式(8),式(9)和式(10)联立求解,并依据理想气体状态方程得到
(11)
其中,L(m)是管子的长度;Rtube(m)是管子半径;Mmol是空气的平均摩尔质量(29g/mol)。
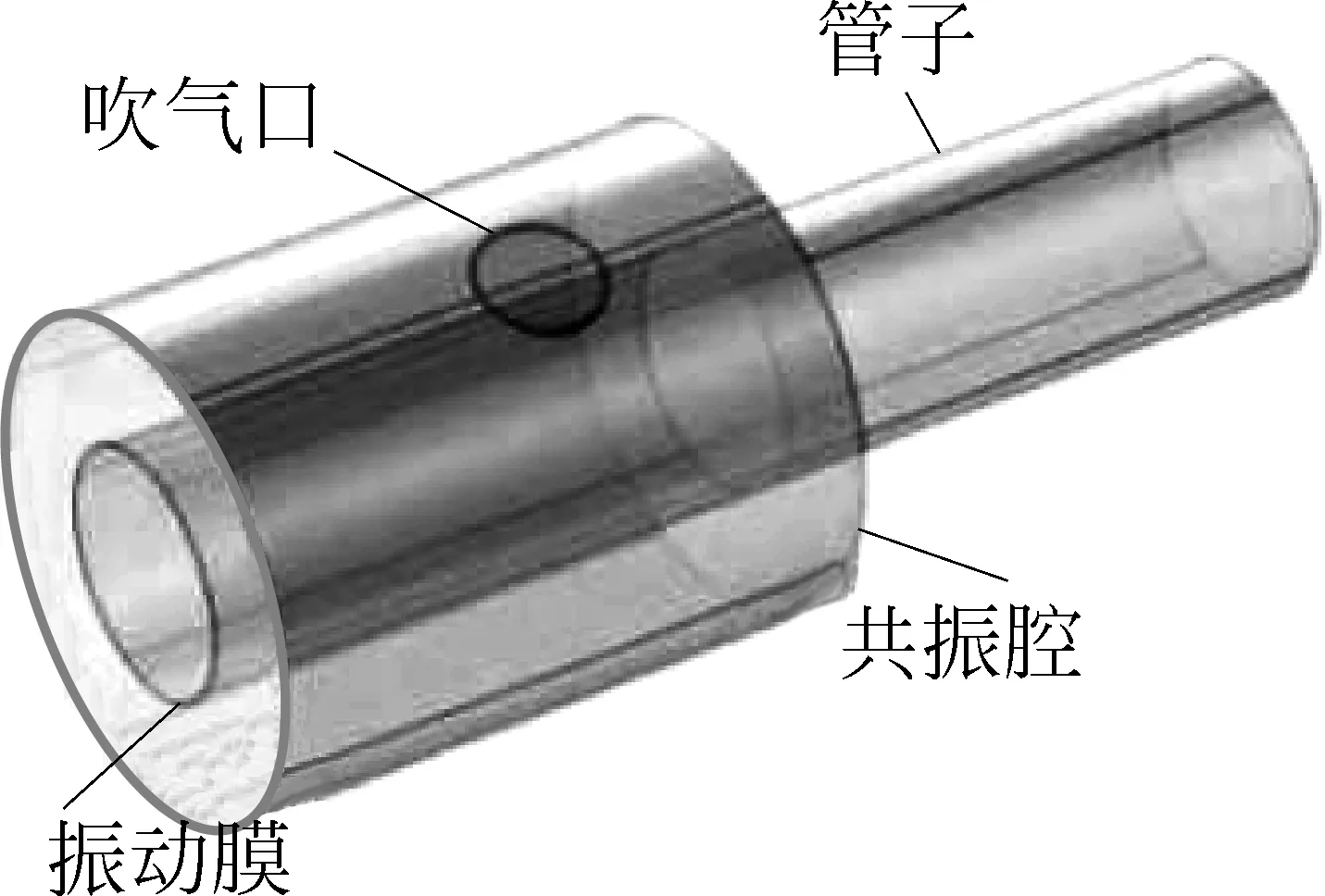
图1 膜簧片型汽笛结构示意图

图2 膜的部分振型(a) x01零阶柱贝塞尔函数的第一个根对应的膜的形状; (b) x02零阶柱贝塞尔函数的第二个根对应的膜的形状; (c) x11一阶柱贝塞尔函数的第一个根对应的膜的形状
式(11)具有柱贝塞尔函数的特征。用Matlab可解出周期函数p(t)的数值解确定周期(图1)。由式(11)可见,当进气质量流速增大时,膜通气时的振动频率减小,且通气时振动频率比固有频率低。
1.2 管子内空气柱振动模型
声音传出不仅通过振膜左侧直接带动空气中的传播,右侧则通过插入的管道中的空气振动进行传播。声音在管道内传播的柱坐标波动方程为[3]
(12)
其中,p(Pa)是声压;r(m)是某点与管子轴线的距离;θ(rad)是该点的方向;z(m)是该点距离膜侧管口的距离;vvoice(m/s)是气体的速度。式(12)的解为[12]
pm=AmJmkrrcosmθ-φmexpjωt-kzz
(13)
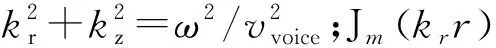
当声源关于轴对称时,会产生造成膜振动频率突变的截止频率,其上界数值可以通过下面经验公式(14)得到
(14)
2 实验部分
在实验中,通过改变气球皮面密度、管子长度与半径、共振腔半径,以及进气速率探究其对声音基频的影响。为了控制实验变量,通过改变阀门的大小控制进气速率。
2.1 实验装置
本实验所用的膜簧片型汽笛是由PVC硬管,气球皮和KT板搭建而成(图1)。采用捷豹OLF-2524空气压缩机(额定排气压力为0.7MPa)来模拟人口吹气,该方式也是实现实验参数的定量化要求。测量压强的设备为EDIS-GPS200。
2.2 声音信号的采集与分析方法
使用SHURE MV51数字麦克风与iPhone手机对声音信号进行采集[11]。声音信号的分析方法是采用Matlab对采集到的声音信号进行频域解析,并在解析前首先用Matlab 降噪工具箱对声音信号进行降噪处理。由于薄膜的频率无法直接通过仪器测量得到,所以用薄膜产生的空气振动频率代替。
3 结果与讨论
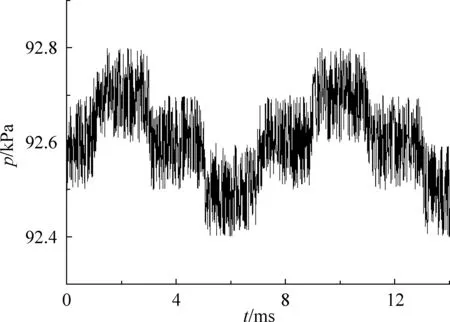
图3 汽笛腔内压强随时间的变化关系
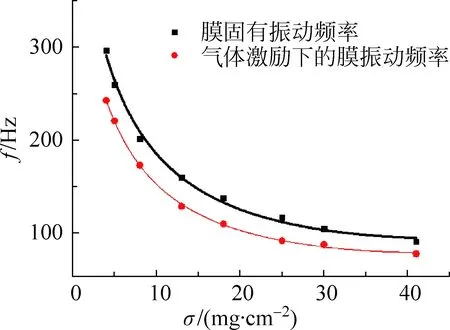
图4 薄膜振动频率与薄膜面密度的关系
图3是膜簧片型汽笛腔内压强即共振腔内部的压强随时间变化的关系曲线。由图3可见,腔内压强随时间作周期性变化。在0~16ms内,腔内气体压强介于92.4kPa~92.8kPa范围内变化,其变化差值为0.4kPa。可以看出,腔内气体压强的变化范围在±0.43%,压强可以看作基本不变,其与振膜的频率一致。
图4是薄膜振动频率与薄膜面密度的关系。由图4可见,随着薄膜面密度从4mg/cm2增加到41mg/cm2时,膜振动频率从243Hz减小到78Hz,分别对实验数据进行二次非线性拟合得到
其中,f固(Hz)是薄膜固有振动频率;f受(Hz)是气体激励下的薄膜振动频率;σ(mg/m2)是薄膜面密度;用R2表示拟合优度,R2的值越接近1,说明回归直线对观测值的拟合程度越好。由于薄膜振动可以等效为在薄膜中心附加一个重物,而薄膜的面密度增大时,这个等效重物的质量也增大。根据阻尼振动方程
(17)
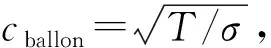
图5是薄膜振动频率与共振腔半径的关系。当共振腔半径由2cm增大到7cm时,气体激励下的薄膜振动频率从168Hz减小到47Hz,分别对实验数据进行非线性拟合后得到关系式为
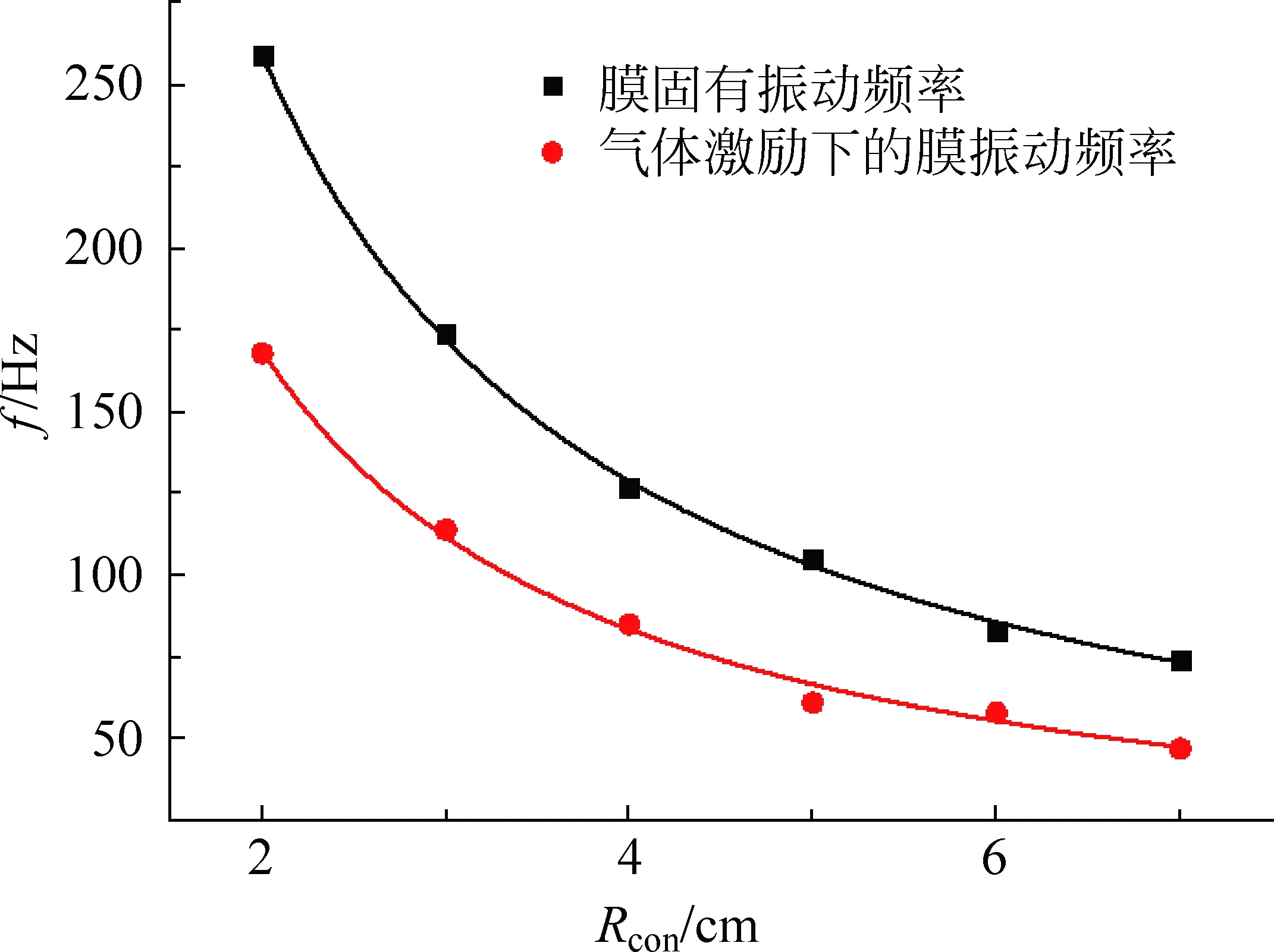
图5 薄膜振动频率与共振腔半径的关系
该结果说明,当Rcon=2Rtube时,共振腔半径对薄膜振动基频的影响,随着共振腔的半径增加,薄膜振动的固有频率和气体激励下的薄膜振动频率都下降。该结果与理论分析的式(4)和式(5)的结果相吻合。另一方面,在一维振动的情况下,共振腔的半径可以等效为振动表面的波长,当共振腔的半径增大时,等效波长也增大。由于扰动在薄膜上的传播速率不变,当共振腔的半径增大时,气体激励下的薄膜振动频率减小。

图6 实际测量的振动频率与管子长度的关系(共振腔的长度为10cm)
图6是实际测量的振动频率与管子长度的关系。当管子的长度由0.12m增加到0.18m时,实际测量的振动频率在211~243Hz之间波动;但是,当管子长度由0.4m增加到1.40m时,实际测量的振动频率从294Hz减小到116Hz。实验得到的趋势与理论分析的公式(4)相吻合。对管子长度由0.4m变化到1.40m范围内的数据进行非线性拟合后得到的关系式为
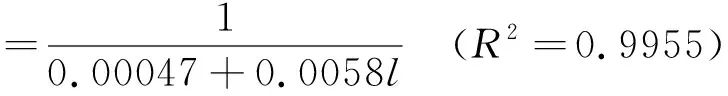
(20)
在一维振动的情况下,管子的长度可以等效为管子内基频的波长,当管子的长度增大时,基频的波长也增大。由于空气中波的传播速率不变,当管子的长度增大时,虽然气体激励下的薄膜振动频率不变,但是,声音的传播通过管子,两种振动的波耦合对外表现为实际测量的振动频率减小。杂乱的点表示在l从0.12~0.18m时f基本不变,所以没有进行拟合,这个时候主要是空气柱振动发声。在气体从汽笛腔体内进入管道时,与管口摩擦形成频率有一定连续宽度的边棱音,边棱音激发管道内气柱形成耦合共振,声音的频率会限制在管子内空气中振动的基频,所以基本不变,但是由于测量误差会有波动。
图7是气体激励下的薄膜振动频率与管子半径的关系。在Rcon=0.02m的条件下,当管子半径RTube由0.40cm增大到1.0cm时,气体激励下的薄膜振动频率从330Hz减小到317Hz,呈现反比关系,与理论部分的式(11)结果相吻合。经过非线性拟合后得到的关系式为

(21)
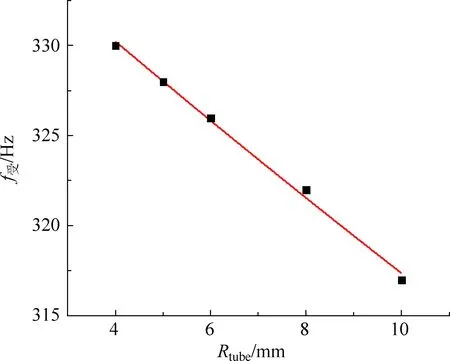
图7 气体激励下的薄膜振动频率与管子半径的关系

图8 气体激励下的膜振动频率与进气速率的关系
图8是气体激励下的薄膜振动频率与进气速率的关系。由图8可以看出,当进气速率在0.4g/s以下及2g/s以上时,采集不到声音; 而当进气速率从0.4g/s增大到1.2g/s时,声音信号的频率从146Hz减小到95Hz,对进气速率由0.4g/s增大到1.2g/s范围内的数据进行非线性拟合后得到关系式为
(22)
当进气速率增大时,气体作用在薄膜上的冲量增加,导致薄膜的振动幅度增大,声音信号频率减小;另一方面,由于管内部的体积可以认为近似不变,进气速率增大必然导致薄膜附近的气体压强增大,气体密度增大,附加质量增大,从而导致声音信号的频率减小。此外,进气速率在1.2~1.4g/s之间时,声音信号的频率存在断层,即从95Hz跃变到56Hz,并且该现象重复性良好,与理论部分的式(14)相吻合。当边棱音接近二倍基频时空气柱振动频率发生跃变。在本实验室所能达到的条件下,影响声音信号频率的部件排序为空气柱>薄膜。
由于膜振动与空气柱振动都是主要声源,当质量流速Q增加时,频率下降,音色改变,当空气柱发声消失时,频率有向低的一次突变的趋势。当薄膜离开管口,在管口附近会出现激波。间断面迅速坍塌产生频率极高的声波,但是,这部分声波会被管道抑制。由于音色主要由高阶的振动决定,并且在管道传声的过程中,声音的高频部分被抑制,所以管道在传声过程中对音色有影响。
4 主要结论
本文解决了基于膜簧片的新型汽笛的频率的影响因素,并且依据理论模型与实验之间的对比,验证了简化模型的正确性。根据理论模型和得到的实验结果,改善了汽笛性能。理论公式中,压强关于时间的表达式无法求解析解和数值解,但能给出变化趋势。对于薄膜而言,当薄膜半径减小,面密度减小,膜张力增大时,声音信号的频率也增大;对于空气柱而言,当管子长度和半径增大,声速减小时,声音信号的频率却减小。但是,半径的影响不是由于它是声源,而是它抑制高频的截止频率的变化和它引发的声速变化的共同作用。总体来看,整体的基频为膜和空气柱的基频交替作用,同时管道传声对高频部分的抑制作用还会改变音色,提高汽笛的性能。

