基于数字仿真的武器平台截获概率特性分析

王亚涛，周龙建，曾小东

(1.中国电子科技集团公司航空电子信息系统技术重点实验室，四川 成都 610036；2.中国西南电子技术研究所，四川 成都 610036)

0 引言

射频隐身是指通过控制自身有源传感器的辐射，降低辐射信号被敌方截获的可能性。常用的手段包括发射功率控制[1-2]、辐射波束控制[3-4]、发射信号波形设计[5-6]和射频传感器协同工作[7]等。为了提高武器平台上有源射频传感器的射频隐身能力，进而提高武器平台的战场生存能力，对各种传感器的射频隐身性能以及全平台的射频隐身性能提出了新的要求[8-9]。在想定场景下，对武器平台的射频隐身能力的评估涉及到整个战场环境，如大气环境[10]；还涉及到多种有源传感器，如雷达[11]、通信数据链[12]和导航设备[13]等。而射频隐身性能的常用表征指标包括截获因子[14]、截获半径[15]和截获概率等。

在诸多表征指标中，截获概率是一项重要指标，它是指对于侦查设备而言，辐射源的信号是未知且非合作的，信号的截获具有不确定性，是一个概率事件[16]。经典的分析方法中将截获概率归结为时域截获、频域截获、空域截获及能量域截获4个方面的窗口函数对准问题[17-18]。这种方法被用于分析一些静态场景下的截获概率问题[19-20]。对实际典型作战场景进行仿真时，战场环境实时变动，这些静态公式不一定有用，因此基于计算机仿真的评估方法受到越来越多的关注[21-22]。基于计算机的仿真方法能够动态地反应出典型作战场景下，武器平台在整个流程中的各个阶段的射频隐身能力，为突防策略的规划提供了一定的指导。因此常常通过时间离散的方法对截获概率进行数字仿真，这等效于重复多次试验后进行统计。本文首先给出了一种数字仿真中截获概率统计方法，并通过静态场景下的解析公式进行验证，最后将该方法运用于动态场景下的武器平台的截获概率特性分析。

1 截获概率计算方法

1.1 截获概率理论计算方法

静态场景中截获概率可以通过理论公式进行计算。静态场景是指辐射源和截获接收机相对位置静止，辐射源波束以一定的扫描速度进行空间扫描，同时工作频率也可以进行跳频变化，而截获接收机以一定的时间占空比进行侦收，其天线波束在空间周期扫描，且以一定的瞬时带宽进行频率搜索。

这种情况下有瞬时截获概率的理论计算公式，即

P=Ptime·Pspace·Pfreq·Pd，

(1)

式中，Ptime，Pspace，Pfreq，Pd分别为时间对准概率、空间对准概率、频率对准概率及检测概率。简单情况下，当辐射源一直处于辐射状态，截获接收机一直处于接收状态，则不需要考虑时域对准概率；认为辐射源波束与截获接收机波束互指，其辐射频率落在当前截获接收机的瞬时带宽内，截获接收机接收能量在灵敏度以上，则为被截获，否则认为未截获。这种情况可仅考虑频率对准与空域对准。

频率对准概率可表示为：

(2)

式中，Boverlap为辐射源工作频率的跳频范围与截获接收机扫频范围的重叠部分；BR为辐射源跳频范围；ΔB为截获接收机瞬时带宽；BI为截获接收机扫频范围。

空域对准概率可表示为：

(3)

式中，ΔθR，θR，ΔθI和θI分别表示辐射源的天线波束宽度和扫描范围、截获接收机天线的波束宽度和扫描范围。这里假定辐射源处于截获接收机扫描范围内，同时，截获接收机也处于辐射源扫描范围内。

1.2 数值仿真中截获概率计算方法

在动态模拟作战场景时，通过将时间离散为一系列的片段Δt，计算每个时间片初始时刻仿真系统中各射频传感器的位置、辐射状态和接收状态等信息，进而统计每种传感器被无源截获接收机的截获状态，并将截获状态记录到数组I(n)中。若截获则认为当前时间片段内被截获，将I(n)记为1，否则记为0。通过多个时间片的仿真得到第N个时间片之前的截获概率P(N)为：

(4)

2 静态场景下的截获概率分析

2.1 频率对准

频率对准概率的仿真中设置辐射源在一定带宽内随机跳频，截获接收机在一定带宽内周期性扫频，此时由于跳频的随机性，使得可以通过长时间段的仿真来计算瞬时对准概率。图1给出了辐射源跳频带宽为1 GHz，跳频时间间隔100 μs，截获接收机扫频带宽4 GHz，瞬时带宽0.5 GHz，扫频速率50 GHz/s，仿真步长10 μs的计算结果。可见随着时间步长的增加，瞬时截获概率逐渐收敛到理论值0.125，证明了仿真的正确性。

图1 频率对准概率

2.2 空域对准

空域对准概率的仿真与频率对准概率的仿真不同。当辐射源的扫描周期与无源截获接收机空域扫描周期相同时，可能出现一直不被截获的情况，即当辐射源波束指向截获接收机时，截获接收机的波束却总是指向其他方向。此时的随机性需要体现在辐射源与截获接收机在初始时刻的波束指向上。采用蒙特卡洛方法，通过随机生成初始波束指向位置，经过多次试验统计，可以得出符合理论结果的瞬时截获概率。几组参数配置下的计算结果如表1所示，可见仿真结果与理论值吻合良好。

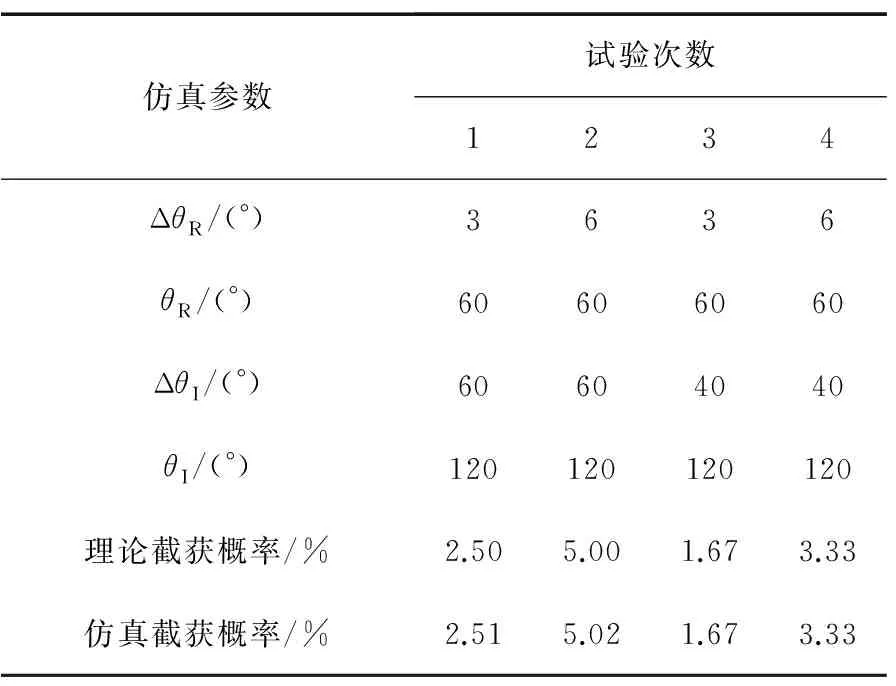
表1 数字仿真与理论计算结果对比

2.3 频域与空域联合对准

对同时考虑频率对准与空域对准的情况也进行了仿真，并与理论公式对比。结果如表2所示。可见，数字仿真和理论计算结果吻合良好，说明了计算的正确性。

表2 数字仿真与理论计算结果对比

3 动态场景下截获概率仿真计算

3.1 仿真方法

采用类似的方法可以对动态场景下的截获概率进行计算。与静态场景不同的是，动态场景下武器平台具有相对运动，在距离较远时由于辐射源辐射功率有限。当截获接收机接收到的功率不能达到截获接收机灵敏度时，即使频域与空域均对准也不发生截获。此外，一般平台上会集成多个传感器，而平台整体的截获概率将由多个传感器的截获概率合成而来。

对于整个平台而言，认为只要有一个传感器被截获则全平台被截获。所以，在某一时间片内，全平台的截获状态IT(n)可以表示为：

(5)

式中，M为传感器个数，而Im(n)为第m个传感器当前时间片内的截获状态。则到第N个时间步为止，全平台的截获概率PT(n)可以表示为：

(6)

这里统计了每个时间片内平台的瞬时截获状态。由此，不仅可以统计最终整个任务过程的截获概率，还可以统计任务过程中任意一个阶段的瞬时截获概率，即

(7)

式中，N1和N2表示某一阶段的起止时间片编号。

3.2 仿真实例

3.2.1 场景描述

下面对一动态场景下平台的截获概率特性进行分析。设单机对抗状态下，红方通过雷达进行扫描探测，同时与卫星进行通信，且进行敌我识别应答。蓝方通过无源截获接收机侦收，红蓝双方飞行高度均为10 km。初始距离300 km，均以300 m/s的速度相向飞行，仿真场景如图2所示。

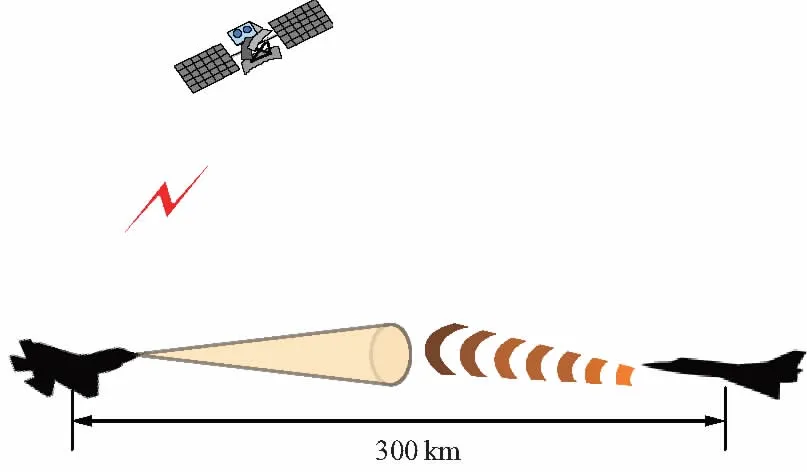
图2 仿真场景示意

仿真中设置雷达等效全向辐射功率(EIRP)为100 dBm，方向图波束宽度3°，副瓣电平-15 dB，接收机灵敏度-130 dBm，工作时搜索20个波束位置。设置卫星通信天线EIRP为87 dBm，由于波束指向天空，始终为副瓣对准截获接收机，其副瓣电平-15 dB。敌我识别采用全向天线，设置发射EIRP为50 dBm。无源截获接收机采用全向接收天线，频域宽开，接收机灵敏度-80 dBm。

3.2.2 单传感器截获概率结果

各单传感器的仿真结果如图3和图4所示。

图3 无功率控制时各传感器截获概率

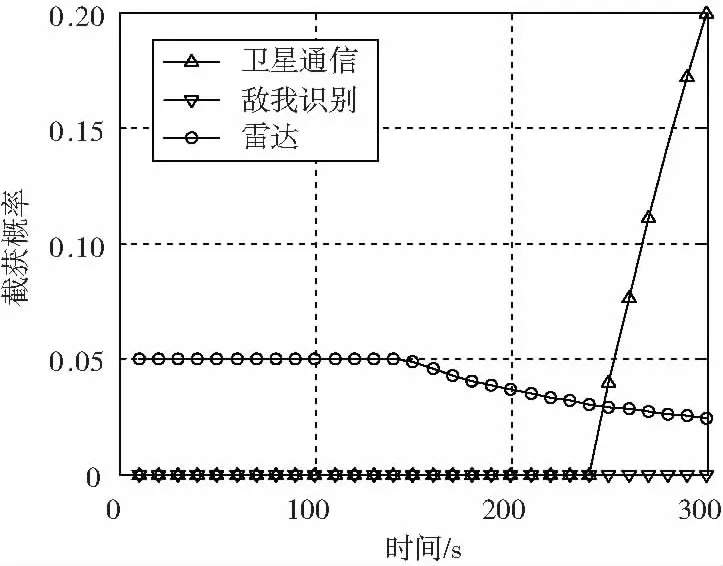
图4 有功率控制时各传感器截获概率

图3为无功率控制情况下各传感器的截获概率特性。可见，其中雷达的截获概率最大，其次为卫星通信天线。而敌我识别由于具有最小的等效辐射功率，在全过程中均未被截获。雷达从300 km远处一旦开机，则主瓣就可能被截获。由于仿真中设置雷达周期性地扫描20个波束位置，因此在副瓣未被截获前的瞬时截获概率为0.05。随着双方平台逐渐靠近，雷达副瓣被截获，统计得到的截获概率迅速增加。

功率控制情况下的截获概率特性如图4所示，其中卫星通信由于通信距离基本确定，未进行功率控制，而敌我识别则由于本身发射功率较小，仍然在全过程中未被截获。不同的是雷达的截获概率首先保持平稳，随后有下降趋势，这是由于双方平台间的距离小于雷达的低截获探测距离后，雷达可以探测目标，而目标上的无源截获接收机却不再能截获雷达主瓣，更不能截获雷达副瓣。可见功率控制的优势。

3.2.3 多传感器截获概率结果

通过式(5)和式(6)，根据以上各传感器的截获概率特性可以计算多传感器的总截获概率特性。结果如图5所示。可见当无功率控制时，多传感器的截获概率与雷达的截获概率相同，这是由于此时各个阶段雷达辐射强度均最大，当有传感器被截获，雷达必然被截获。而功率控制下的多传感器截获概率则是由各传感器结果的合成效果。即约250 s以前主要由雷达贡献，250 s以后主要由卫星通信传感器贡献。

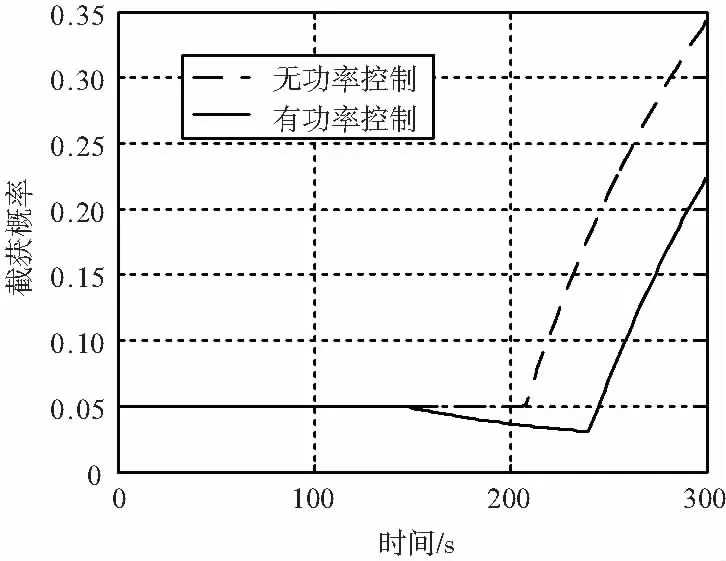
图5 多传感器截获概率特性

此外还采用式(7)的分段统计方式统计了不同阶段的截获概率。统计过程中以30 s时长为一周期，结果如图6所示。

图6 多传感器截获概率特性

可见采用分段统计后可以显示出各阶段的瞬时截获概率。150 s以前由于只有雷达主瓣被截获，存在空域对准，因此截获概率较低。在240 s以后，卫通天线副瓣持续对准，截获概率达到1。还值得注意的是，通过功率控制后，在150～200 s的时间段内截获概率为0，说明此时间段内没有传感器被截获，这些细节在图5中不能反映出来，说明了分段统计的优势。

4 结束语

本文对数字仿真技术中截获概率的统计计算进行了讨论。通过静态场景仿真验证了截获概率统计的正确性，然后将该方法推广到动态场景的仿真中。同时给出了通过多传感器的截获概率计算全机截获概率的方法，使得能够通过后期数据处理，方便地统计任意时间段内的瞬时截获概率，以便对对抗流程中各阶段的射频隐身特性进行更加精细的分析。最终结合具体算例对所提出方法进行了分析验证，说明了本文方法的有效性。