扩展原模图AR4JA编码的优化构造

马 慧，吴彦鸿，王宏艳

(1.航天工程大学 电子与光学工程系，北京 101416；2.航天工程大学 航天信息学院，北京 101416)

0 引言

20世纪60年代以来，前向纠错(Forward Error Correction，FEC)一直是空间通信的重要组成部分。随着超大规模集成电路技术的发展，相比于现有Turbo编码，LDPC编码能够更好地实现译码复杂度和误码平层之间的性能折衷，这无疑更适合下一代高速数据通信中的FEC[1-2]。尽管LDPC编码性能逼近香农极限，但香农编码只能给出理论结构，未能提出具体构造方法。校验矩阵的结构是LDPC编码过程的构造基础，不仅直接关系到编码性能的优异程度，还会对系统的编译码复杂度产生影响[3]。

现有LDPC编码主要通过几何、代数和图论等构造方式构造[4-5]，例如基于欧拉图结构的图论构造法[6]、基于双对角矩阵的序列构造法[7]和基于停止集优化的原模图构造法[8]等，其中原模图构造的LDPC编码在目前的通信卫星、遥感卫星、导航卫星和星际探测等一系列航天活动中发挥重要的作用[9-10]。根据构造主体的不同可将原模图构造编码的研究分为2类:原模图模板矩阵的构造和原模图循环移位子阵的构造。模板矩阵的构建对于不规则LDPC编码来说至关重要，文献[11]提出的启发式渐进增加边(Progressive Edge-Growth Graphs，PEG)算法改善了Tanner图围长分布特性，近年来被广泛应用于矩阵构建过程。文献[12]构造了一种具有优异性能的低码率通用LDPC编码，但对于模板矩阵准循环结构的利用仍不充分，并且为有效解决基于原模图编码的秩亏现象，占用了特殊编码结构，这无疑增加了编码的复杂度。文献[13]通过欧式几何优化方法对准循环结构中的最小重码字进行优化。文献[14]设计多边原模图消除QC结构中无法避免的小环，文献[15-16]通过改善多对角线奇偶校验结构及准循环双对角线扩展等方法得到较好性能的码字。文献[17]通过扩展的ACE算法对原模图信息节点进行重新排序，在不损坏准循环结构的同时，克服了秩缺失问题。但是该方法在构造时需要对环进行搜索和结构分析，仍旧存在一定的复杂性。文献[18]对原模图结构进行优化设计，克服了AR4JA编码误码平底现象。文献[19]提出采用PEG-ACE两步扩展法对原模图扩展后的循环子阵进行环结构优化，虽然经PEG-ACE算法扩展后得到的AR4JA编码的复杂度明显降低，但是该算法中PEG扩展过程忽略了备选节点的考虑，节点度分布距离最佳分布仍旧存在差距；ACE扩展过程缺少对嵌套原模图中块环结构分析，算法性能存在一定的误差和误码平层现象，因此需要对其加以改进。本文提出了一种基于原模图扩展的AR4JA码优化构造方法。针对原模图结构对应的基矩阵，提出改进的PEG扩展和QC-ACE优化搜索循环置换子矩阵偏移量，联合优化与改善编码码字的围长及环分布关系，使其适用于原模图的扩展，提高码字的误码率性能。

1 AR4JA编码的原模图构造

1.1 原模图构造基本原理

目前由原模图构造的LDPC编码在通信卫星、遥感卫星和星际探测等一系列航天活动中广泛应用，将原模图用变量G=(V，C，E)表示，其中V表示变量节点集，C表示校验节点集，E表示连接边集合。将变量节点ve∈V和校验节点ce∈C之间存在的连接边定义为e∈E，由于原模图允许平行边的存在，连接边映射e→(ve，ce)并非是一一对应的。

本文针对原模图LDPC编码的原模图构造展开分析，原模图与Tanner图的不同之处在于原模图可允许并行边的存在，因此其结构中一般具有少量的节点[20-21]。原模图的复制模板图G如图1所示。

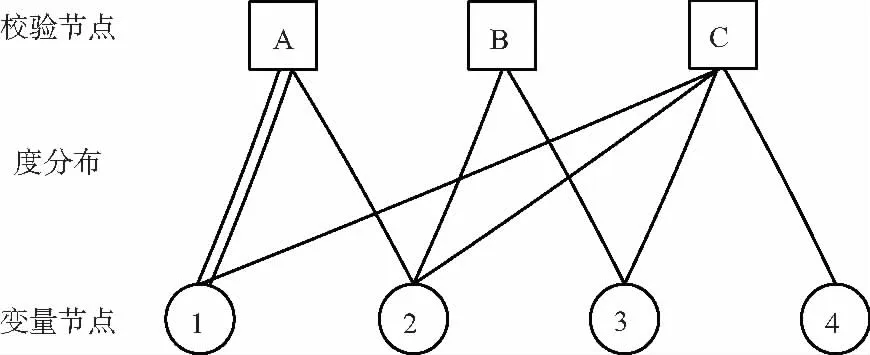
图1 原模图的复制模板图G

该原模图可被视为在(n=4，k=1)LDPC编码Tanner图的基础上添加并行边得到的。G是由|V|=4个变量节点和|C|=3个校验节点组成，其中变量节点包括节点1～4，校验节点包括节点A～C，共有|E|=9条连接边。G中节点对应的校验矩阵HG的表达式为：

需要强调的是，不同于Tanner图中的映射暗含着每个变量节点必然对应传输信道中的一个编码符号的假设，原模图中的变量节点集V可以包含未发送节点，未发送变量节点的采用可改善原模图编码的性能。因此变量节点vi∈V可被指定为发送节点或未发送节点，定义变量节点中发送节点的个数为n，未发送节点的个数为u，则

n+u=|V|。

再定义校验节点个数为c=|C|，则原模图编码后的码率为：

将原模图模板中的校验节点和变量节点进行L倍复制，可得到由L份相互重叠的副本构成的子图。再按照一定的规则，将各个副本中对应相同位置的连接边进行置换重排，得到的交织图称为扩展衍生图，由此构造的LDPC编码称为原模图LDPC码。以图1为例，对模板G进行3次复制并置换后得到的衍生图G′，如图2所示。可看出衍生图G′继承了原模图的特性，具有与G相同的码率、节点度分布以及邻域特性，因此二者的译码门限相同。

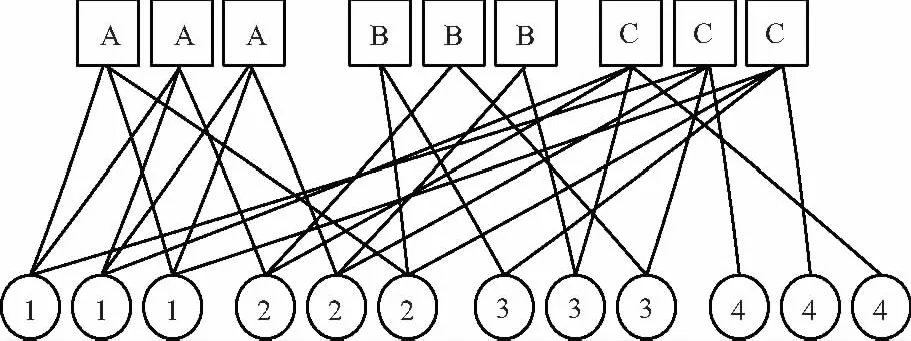
图2 原模图置换后的扩展衍生图G′

将原模图LDPC码对应一致校验矩阵一般通过基矩阵和循环置换矩阵联合表述，当设定置换矩阵的维数p时，H与基矩阵和循环移位矩阵的对应关系为：

-1≤hi，j≤p-1。

式中，矩阵I(hij) (1≤i≤m，1≤j≤n)为p×p维循环置换矩阵；hi，j为单位矩阵I的循环移位位数，其中当hi，j=-1时，I(hij)为零矩阵；当hi，j=0时，I(hij)为单位矩阵I；其他情况下，I(hij)表示单位矩阵循环右移hi，j位后的矩阵。由于H中循环矩阵和零矩阵的位置取决于基矩阵的设置，而置换矩阵决定着单位矩阵的循环移位位数。由于原模图构造的校验矩阵在本质上决定了码的性能，因此对AR4JA码性能的优化离不开原模图的构造。

1.2 AR4JA编码原模图的模型构建

AR4JA编码的原模图构造流程表述如下：

① 结合模拟退火算法及密度进化理论进行原模图译码搜索的门限预测，所设计的AR4JA对应的原模图构造原理图如图3所示[18]。图中代表信息比特的圆形节点分为2种，其中灰色实心圆表示待传输的变量或者校验比特，白色空心圆表示非传输的删除比特；内含加号的方框表示校验节点。以矩形框内1/2码率AR4JA编码原模图模板为基础，在矩形框外部扩展校验节点关联复合变量节点可实现编码的码率扩展，得到的AR4JA系列码率表达式为：

(5)

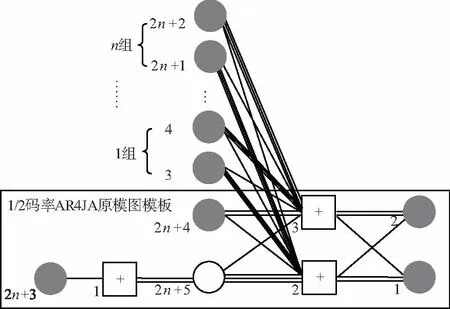
图3 AR4JA编码原模图构造原理

② 图3所示的AR4JA编码原模图模板允许多重边的存在，因此需要对其进行平行边的消除使其转变为Tanner图结构。首先将该原模图作为QC-LDPC结构中的基本Tanner图模板，对其进行矩阵复制操作以得到L个副本，然后对复制后原模图中各对应边重排扰乱，使不同副本间节点互连，从而得到所需规模的Tanner图。在此需要注意的是，在对不同副本中相同位置的连接边随机扰乱的过程中，连接边对应两个模板间的节点序号需要保持不变。

③ 将构造的Tanner图映射为校验矩阵H的形式，图中的方框节点对应H的行，圆形节点对应H的列。当节点之间存在连接边时，对应H相应位置为“1”；反之则为“0”。然后将H的基矩阵进行扩展得到所需的循环移位矩阵，也就是将“0”、“1”分别映射为一定维数的全零阵或者单位循环方阵。矩阵扩展结构的物理实现过程可通过图4所示的立体Tanner图模型表示。

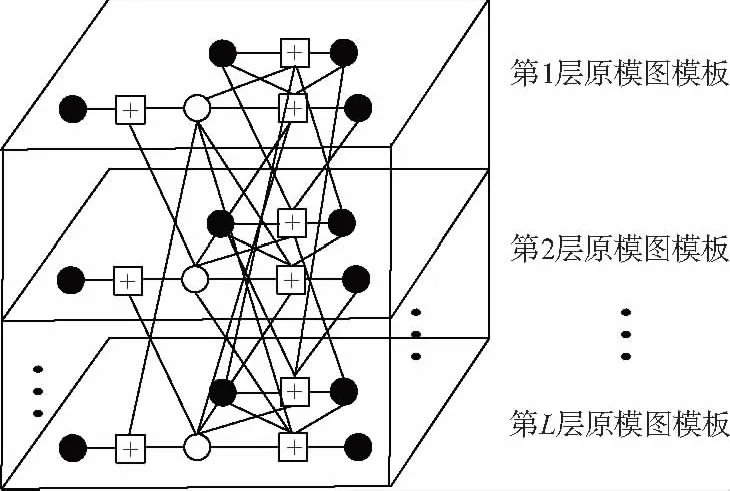
图4 AR4JA编码原模图立体Tanner图模型

由图4可知，经过空间扩展后的Tanner图既继承了基本原模图的性质，具有和初始原模图模板相同的连接关系和度分布，还存在一定的空间交织结构使其具有增大码距的效果。复制扩展后的原模图既继承了原模图模板的基本性质，又增加了编码随机度，因此可将其作为构建高效能不规则LDPC编码的有效方法。通过对模板基矩阵进行循环扩展再分裂，可进一步消除停止集及状态恶化的陷阱集，环分布的自由度也得以改善。

2 两步扩展原模图编码的优化构造

要想得到性能优越的AR4JA码，仅仅设计出原模图是不够的，还需要对校验矩阵的环结构进行分析。基矩阵中的“块环”作为扩展矩阵不同环之间的连接基础，是决定译码性能的关键因素之一。当基矩阵对应的块环长度相同时，矩阵扩展后的环长与循环移位值和移位子阵维度p有关。因此在准循环编码的构造过程中，原模图的既要考虑基矩阵的设计，又要兼顾循环置换矩阵的设置。文献[11]将原模图的构造分成两步扩展进行，先采用PEG算法寻找具有最佳围长参数；然后通过QC-ACE算法搜索子矩阵循环偏移量，以最大限度延长矩阵中的环长，所构造的码字具有复杂度低、结构性好的特点。但是在运用PEG算法时，未对备选节点的选择分情况讨论，因此度分布距离最佳分布有一定差距；QC-ACE算法中未考虑嵌套环条件下的算法误差性能，两步扩展算法仍旧存在优化空间需要进一步对编码性能进行优化。

2.1 改进的PEG扩展算法

传统PEG算法构造基矩阵时，仅局限于围长最大化，未对备选节点的选择分情况讨论，因此度分布距离最佳分布有一定差距。因此为了进一步优化基矩阵的环连通性，需要考虑多个备选节点情况并加以讨论。文献[22]将节点的ACE值作为环连通性的测度，并引入了ACE选择准则：当中至少包含2个元素时，选择使得引入的环具有较大ACE校验节点与vi连接。受该准则的启发，本文对PEG扩展算法进行改进。

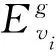
表1 改进的PEG基矩阵扩展算法原理

上述PEG算法中，满足原模图扩展约束的校验节点随着每一条边的扩展变化，由于在Tanner图不允许出现重边的出现，所以在扩展原模图时要保证扩展层数不低于最大重边数。

2.2 改进的QC-ACE算法

在搜索原模图构造矩阵中的循环偏移量时，QC-ACE算法忽略了嵌套环中公共节点的存在，使得到的实际变量信息的ACE值产生偏差。采用改进的QC-ACE算法时，针对Tanner图中的环间关系分情况讨论，对于不存在重边的原模图直接采用原环间ACE值进行准循环扩展，对于嵌套环情况时，采用改进的复合环系统的ACE值进行计算。该ACE值的本质是指嵌套环的外部独立有效连接边，因此在累积计算各环路节点ACE值之后，需要减去公共环中的重复ACE值，以避免外消息传递自反馈导致译码性能变差。

首先对算法中的专业名词及符号进行说明，分别定义当前层根节点及与其相邻的子节点为ws和Z(ws)，节点vi和cj分别表示AR4JA编码矩阵中的变量节点和校验节点。函数p(μt)表示根节点与任意变量或校验节点之间所有节点ACE值总和。设编码的门限参数为(dACE，hACE)，即所有环长不大于2dACE的环的EMD值至少为hACE。在LDPC编码对应的子循环阵中，设横向及纵向最大非零矩阵块数分别为n，m。改进的QC-ACE算法步骤如下：

① 初始化。根据置换子矩阵的分布，按照从右至左、自上而下的方向搜索非零循环子阵，并在对应位置随机产生变量节点vi，即随机产生所在行“1”的循环右移位数；预设所有节点为活跃节点。

② ACE检测。在进行ACE检测之前，分别对单环和复合环对应的ACE表达式进行定义。其中变量节点vi对应的ACE为：

ACE(vi)=di-2，

(6)

式中，di为环中变量节点vi的度。则变量节点vi所在的单环ACE的表达式为：

(7)

但该表达式不适合公共边的复合环，因此针对而复合环需要重新定义ACE计算式。用C(vi)表示复合环中变量节点相连的校验节点集合，其中元素数量记为n(C(vi))，设a表示复合环中的公共节点取值范围，则复合环ACE计算表达式为：

(8)

设定变量节点vi为根节点ws，寻找ws邻接子集Z(ws)中的校验节点cj，则该节点当前的ACE路径为：

ptemp=p(ws)+ACE(cj)。

(9)

该节点的环长可通过节点先前最小ACE路径及当前到该节点ACE减去根节点及子节点的2倍计算，则当前构造环长为：

ACEtemp=ptemp+p(μt)-ACE(vi)-ACE(cj)。

(10)

③ 若满足约束条件环长L≤2dACE时继续进行ACEtemp≥ηACE；反之，说明本次搜索失败，需要重设初始化参数，再次进行搜索。

④ 重复步骤②，对基矩阵中非零元素进行遍历，当所有非零元素都满足ACE约束时，循环矩阵的构造完成，原模图的第二步扩展结束。反之，则返回步骤①。

在搜索过程中，由于初始化参数设置带有随机性，需要搜索多组码字进行验证，以最终确定循环偏移参数。

3 仿真实验与性能分析

为验证基于PEG-ACE优化的AR4JA构造算法性能，将本文提出的优化算法构造得到的AR4JA编码分别与随机构造算法以及现有AR4JA编码性能进行对比。假设信道为AWGN信道且噪声功率密度为N0，调制方式采用BPSK。译码采用标准BP译码，对于每帧LDPC译码中最大迭代次数设置为80次，在每个信噪比条件下将实验运行到指定的误帧数或者实验次数达到107量级。

3.1 与随机构造编码比较

首先用PEG-ACE优化算法构造1/2码率的(2 048，1 024)AR4JA编码，再用PEG经典构造法构造的相近码长的(2 016，1 008)全随机LDPC编码作为对照[23]，对比结果如图5所示。

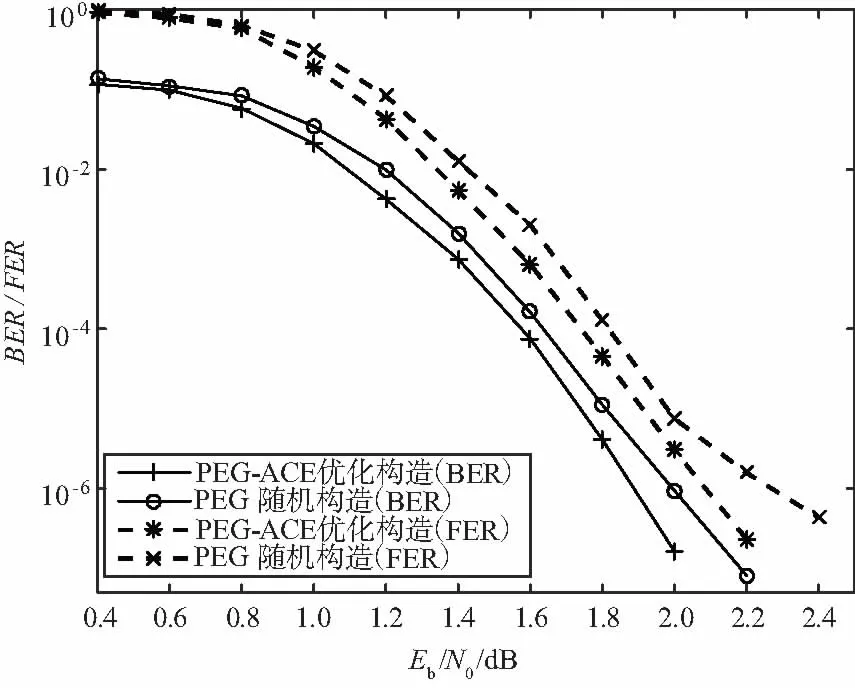
图5 随机构造编码与本文构造编码性能对比

可看出全随机LDPC编码随着信噪比的增加存在着一定的误码平层现象，而本文中采用两步扩展优化搜索算法构造的编码，最短围长和环连通特性得到改善，有效克服准循环LDPC编码中存在的误码平底现象，编码的综合性能得到改善。

3.2 与现有AR4JA编码比较

首先用PEG-ACE优化算法构造4/5码率的(1 280，1 024)AR4JA编码，再用现有PEG-ACE算法构造法AR4JA编码作为对照[19]，对比结果如图6所示。

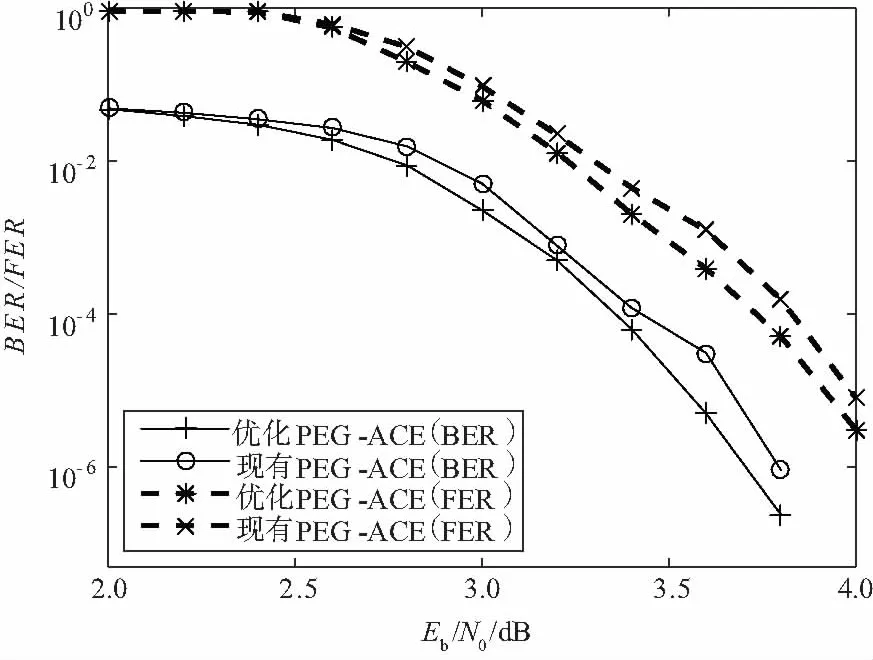
图6 现有AR4JA编码与优化构造编码性能对比

图6的仿真结果表明，在类似仿真参数及误比特率条件下，优化构造的AR4JA编码略优于现有的AR4JA编码。现有AR4JA编码采用PEG算法时未考虑备选节点，且对应的Tanner图中存在部分嵌套环，易引起环间信息传递自反馈导致的误码。经过PEG-ACE优化算法可改善环间独立节点信息，从而改进译码性能。同时在复杂度相似的前提下，采用两步扩展优化算法可获得微小性能的改进，具有较好的工程实践意义。

4 结束语

本文提出了扩展原模图的AR4JA编码优化构造算法，根据AR4JA编码原模图模板，对校验节点及其关联的变量节点进行扩展，增加矩阵维度。在扩展过程中，以环长和环路ACE测度最大化为目标，提出了PEG-ACE优化算法，在译码门限和误码平层方面都具有良好表现，适合空间卫星通信应用。同时，所构造的LDPC编码具有准循环结构，易于工程实现。