基于窄带RCS的空间目标尺寸识别

周 驰，李 智，徐 灿

(1.航天工程大学 研究生院，北京 101416；2.航天工程大学 航天指挥学院，北京 101416)

0 引言

随着人类航天事业的不断发展，作为“高边疆”的太空日益成为世界各国争夺的焦点，以监视太空资产、太空碎片和太空活动为目的的空间目标监视系统成为各国重点建设的对象，其中关键的组成部分是地基和天基探测设备[1]。由于地基雷达系统具备可全天运行，受天气、光照条件影响小等特点，在空间目标监视系统中发挥着重要作用[2]。

随着雷达技术的不断发展，基于雷达的目标识别技术成为现在研究的热点问题。目前，雷达主要有以下几种测量技术：RCS测量技术、多频测量技术、极化特征测量技术和高分辨率技术[3]。目前，窄带雷达成本较低，易于研制，数量较多，可以产生大量的空间目标窄带数据，其中空间目标雷达散射截面(Radar Cross section，RCS)序列包含丰富的信息，对于科学研究与目标识别具有重要意义[4]。如果能利用RCS进行目标识别，将大大提升我国太空监视能力，而且RCS具有数据量小、处理方法简单等特点，因此这一直是目标识别的方向之一[5-6]。然而空间目标RCS受目标形状、姿态以及散射特性等多因素影响，导致空间目标RCS时间序列为非平稳信号[7]，加大了数据处理的难度。目前利用传统模型(Size Estimation Model，SEM)仅能估计出空间目标的一维尺寸，难以满足军民需求。

本文探究了利用STK和RCS计算程序为核心的动态RCS序列生成方法，能快速获取目标高精度动态RCS序列。基于椭球体模型，提出了一种估计空间目标尺寸方法，仿真数据表明此方法可以快速、有效识别空间目标尺寸，对于空间目标识别有借鉴意义。

1 动态RCS序列生成方法

识别与反识别洲际导弹真假弹头、隐身飞行器的隐身与反隐身等需求掀起了RCS研究的高潮，随着对于雷达目标电磁散射特性研究的不断深入，研究人员提出一系列RCS预估方法(几何光学法、一致性绕射理论、积分方程法和物理绕射理论等)[8]，进行了大量暗室、外场实验，使得目标静态RCS数据不断完善。

然而，静态数据无法反映动态的雷达特性和雷达获取数据的时序信息[9]。随着雷达技术的不断发展以及需求的不断提高，静态RCS数据逐渐无法满足需求，对于雷达目标动态RCS序列的获取和研究变得至关重要[10]。

1.1 生成动态RCS序列的传统方法及问题

目前，获取目标动态RCS数据主要有3种方法：实际测量、暗室测量以及理论仿真。其中，实际测量得出目标RCS序列真实数据，利用价值极高，但是实际测量存在以下问题：① 大量数据掌握在军方手中，由于保密因素，难以获取；② 针对非合作目标由于难以得到目标姿态、结构数据，RCS数据利用率不高；③ 测试场地占地大，成本高。

暗室测量建设成本较高，对于暗室硬件条件要求较高，大样本测试不易进行[11]。并且室内缩比模型的RCS值也需要和真实值之间建立映射关系。

随着RCS仿真技术的不断发展，由于其数据准确、可大量生成、模型多以及成本低等特点，利用仿真技术获取动态RCS 序列成为研究热点[12-13]。目前生成动态RCS序列的方法首先需要建立目标全角度RCS静态数据，之后建立目标航迹(轨道)模型，利用坐标转换，获得雷达在目标本体坐标系下的姿态角，根据姿态角从全角度RCS序列中挑选出相应数据，最终形成动态RCS序列。这种方法步骤繁琐，效果不是很好。

1.2 动态RCS序列生成方法

针对传统方法需要进行繁琐的坐标转换以及生成全角度RCS序列的问题，本文利用STK姿态动力学模块与RCS计算程序为核心生成动态RCS序列，具体流程如下：

① 利用3维建模软件建立空间目标模型，如图1所示。

图1 建立卫星模型

② 将空间目标模型导入到STK中，生成STK场景，设定空间目标轨道、姿态、稳定模式和雷达部署位置等。

③ 在STK下设定空间目标本体坐标系，固连到目标本体上。通过STK报表获得雷达在此坐标系系下的坐标，得到雷达相对于固连在目标的本体系的角度，进而获取目标相对于雷达的姿态，生成空间目标姿态数据。

④ 将空间目标姿态数据输入RCS计算程序中。本程序利用基于改进 Gordon方程的 RCS快速算法[14]，此算法对模型面元进行预处理，提高了运算的效率。结合目标姿态数据，生成空间目标动态RCS序列。

该方法利用STK轨道动力学与姿态动力学模块，解决了传统方法需要进行繁琐的航迹规划与坐标转换的问题，并且不需要生成全角度RCS序列。可根据实际情况建立空间目标模型，快速生成动态RCS序列。大量仿真动态RCS序列的生成，解决了实测数据不易获取以及非合作目标的问题，便于对RCS时间序列研究的推进以及识别模型的建立，有利于从RCS中挖掘出有用的信息，满足现实需求。

2 空间目标尺寸识别模型

在基于RCS序列进行目标尺寸估计方面，法国的 G.Y.Delisle 提出基于单频—全角度RCS数据的几何尺寸估计[15-16]。美国林肯实验室应用大量RCS实测数据，将空间碎片等效为球体，建立了空间目标尺寸模型(SEM)[17]。通过改进，提出椭球体模型，如图2所示，利用划定门限的方法估计椭球体的长轴短轴进而得到空间碎片尺寸。在此基础上，国防科技大学黄小红提出了一种划定门限的方法[18]，用来估计空间目标尺寸。但是这些方法需要形成RCS与目标尺寸的映射关系，这需要大量的实测数据，但由于实际情况限制，实测数据并不容易获取。并且特征尺寸映射模型存在误差，通过此模型将RCS序列中每个值都转换为尺寸再进行处理加大了估计误差。国防科技大学于春锐提出不需要建立RCS与目标尺寸的映射模型的尺寸估计方法，但是没有考虑频率对于RCS的影响[19]，导致此方法只能在光学区应用，并不能适用一般情况。文献[20]将中段目标等效为椎体进行尺寸估计。

图2 空间目标椭球体模型

虽然将空间目标等效为椭球体会丢失空间目标的一些信息，但是经过工程应用验证，此简化模型具有实用价值，较SEM模型针对性更强。林肯实验室研究表明，动态RCS序列的均值与标准差对于估计目标尺寸十分重要[21]。本文将以空间目标RCS序列均值与标准差为核心，将空间目标等效为椭球体，建立空间目标尺寸识别模型。

2.1 尺寸映射模型

本文利用动态RCS序列对空间目标尺寸进行识别，其中确定RCS值与空间目标特征尺寸的映射关系是需要解决的基础问题，即建立空间目标尺寸映射模型。

选择P波段雷达信号对不同半径的金属标定球进行RCS序列仿真。利用三维建模软件建立半径为0.5，1，2，5，10 m球模型，导入到RCS计算程序，生成RCS序列，如图3所示。

图3 不同半径球体RCS序列

理论上，球的RCS值为定值，仿真数据出现波动是因为三维建模软件并不能生成完美的球体。其中90°出现较大波动是因为X-Y平面处面元少，分布稀疏，如图4所示，这导致面元间不共面，而本文选用的RCS快速算法同样是将曲面近似平面处理后获取的，所以会导致出现误差。

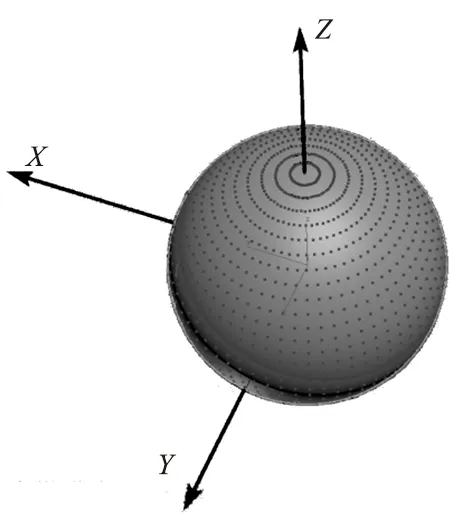
图4 球体面元分布

其中半径为5 m的球RCS序列较其他球体数据不稳定是因为随着球表面积的增大，面元数不变导致对建模软件球体的描述变差，随着提升面元数，大半径球体RCS趋于稳定(如图3中半径为10 m的球体)。针对以上情况，本文选择RCS序列均值作为球体RCS值，特征尺寸-RCS映射表如表1所示，利用插值逼近法建立尺寸映射模型如图5所示。据此由空间目标特征RCS值确定空间目标特征尺寸

表1 特征尺寸-RCS映射表

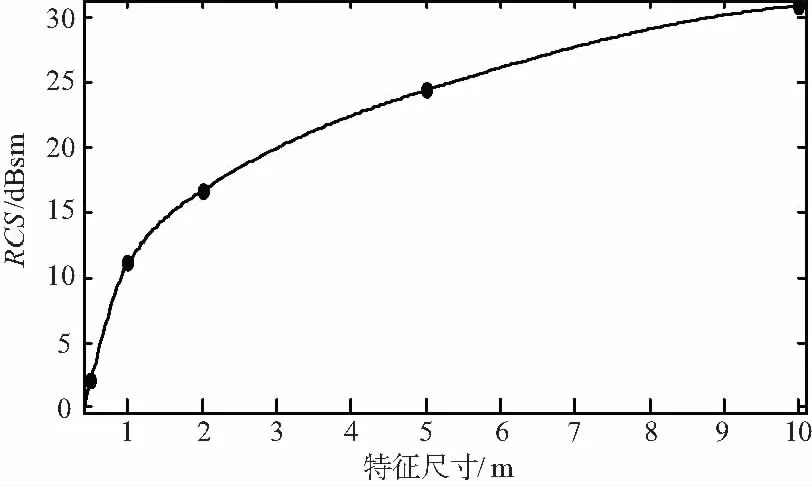
图5 尺寸映射模型

2.2 轴比估计模型

传统方法划定门限区分RCS序列，大值代表长轴，小值代表短轴。但是由于RCS的特性，一些特殊结构会造成RCS值的缩减，如果直接利用小值代表短轴，会造成空间目标短轴尺寸识别的不精确。研究表明，动态RCS序列的方差可以代表空间目标的轴比信息，因此，本文采用求解轴比与长轴尺寸的方法，对空间目标尺寸进行识别，需要建立轴比估计模型。

有研究表明，轴比一定的情况下，椭球体RCS序列方差基本不随长、短轴的尺寸变化而发生变化。

将空间目标等效为椭球体，分别对长轴4 m短轴2 m、长轴2 m短轴1 m、长轴1 m短轴0.5 m的3种椭球体进行RCS数据仿真验证，提取仿真数据方差，如表2所示。

表2 轴比为2椭球RCS序列方差

通过表2可以看出，椭球体RCS序列方差具有很强的稳定性，可以作为特征值代表空间目标的轴比。分别选取轴比为1、2、3、4的椭球体，进行RCS仿真与数据处理，结果如表3所示，利用插值逼近法建立轴比估计模型如图6所示。

表3 轴比-方差映射数据表

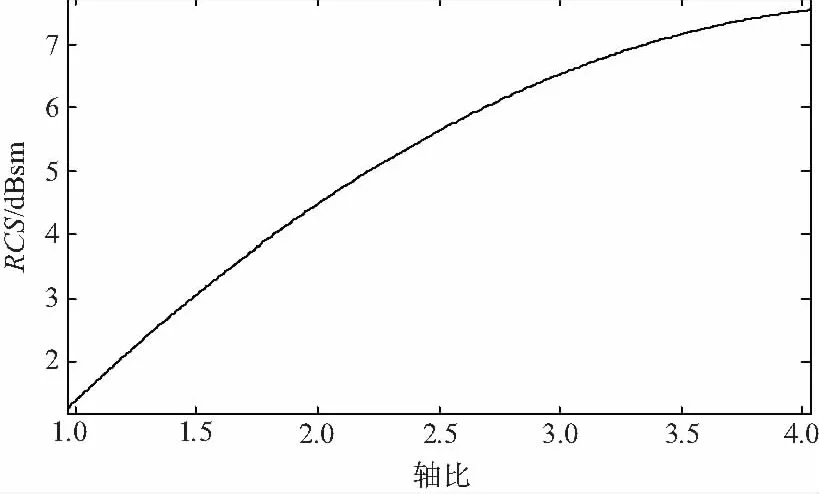
图6 轴比-方差映射模型

2.3 长轴估计方法

根据本文建立的空间目标尺寸识别模型，将空间目标等效为椭球体，通过处理空间目标动态RCS序列来识别目标轴比以及长轴尺寸，进而获取目标长、短轴尺寸，从而识别空间目标的尺寸。动态RCS序列有时会出现一些极大的峰值，这是目标大面积平面相干增强或者角反射器导致，不利于尺寸估计，如图7所示，所以需要在RCS序列中将其去除。

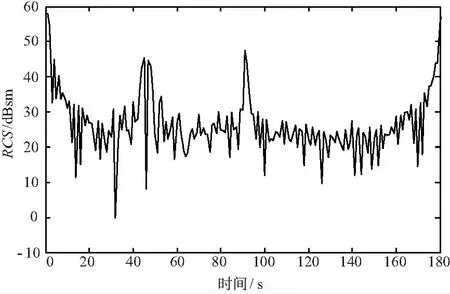
图7 RCS序列中的峰值现象

对于长轴的估计显得尤为重要。目标特征尺寸越长，其RCS值越大[22]，因此在动态RCS序列中，大值可以代表目标的长轴。可以在RCS序列中划定一个门限值。大于门限的部分求平均值代表长轴，划定门限对于估计长轴极为关键。最直接得方法可以采用RCS序列均值作为门限，经过验证，此方法误差较大，需要找到一种门限划定方法。通过2.2小节的分析，方差与轴比有映射关系，并且与空间目标尺寸没有关系。空间目标动态RCS序列方差越大，目标轴比越大，在短轴相同的情况下，长轴越长，门限值越高。所以可以将方差加入到门限划定中，由于在验证中出现误差，本文引入权值进行门限划定。

α=m+βS，

式中，α为门限值；m为空间目标动态RCS序列均值；β为权值；S为空间目标动态RCS序列方差。

其中权值的优化本文利用粒子群优化算法，依据椭球体模型进行优化。适应度函数为依据此模型得到的长轴尺寸与真实尺寸的绝对值，粒子群规模为50，迭代步数取1 000，学习因子取2，惯性权重取0.5。得到权值β为1.5。

3 仿真验证

本文利用第2节建立的空间目标尺寸识别模型对3种目标进行尺寸识别，分别为自旋稳定目标(目标1)、三轴稳定目标(目标2)、简化三轴稳定目标(目标3)，目标模型如图8所示。目标外形参数如表4所示。利用部署在某地的P波段雷达进行仿真数据生成。

(a)自旋目标(目标1)

(b)三轴稳定目标(目标2)

(c)简化三轴稳定目标(目标3)图8 3种目标模型

表4 目标外形参数

利用建立空间目标尺寸识别模型对空间目标动态RCS序列进行处理，处理结果如表5所示。

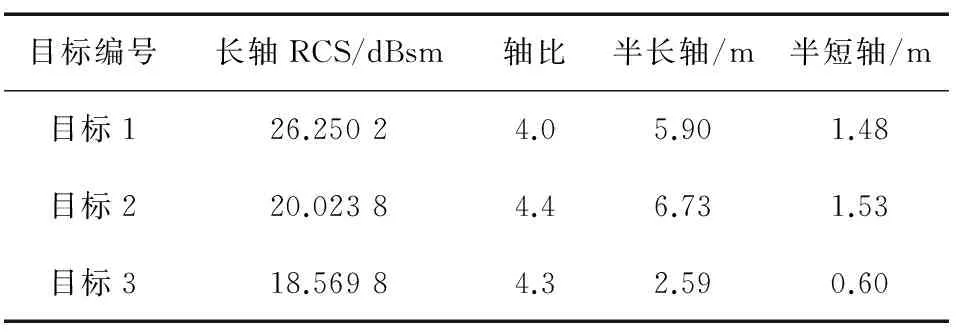
表5 3种卫星尺寸识别结果

通过对利用本文模型识别出的空间目标尺寸与空间目标真实尺寸进行对比可以看出，本模型对于自旋稳定目标识别效果较为理想。其中长轴精度达到98.3%。由运动方式可以得出，本文方法对于失稳卫星以及空间碎片也可以精确地估计其二维尺寸。

对于三轴稳定目标，单站识别出的尺寸出现较大误差，这是由于RCS序列与空间目标姿态有很大关系，在一个观测周期内空间目标姿态稳定。利用随机部署的雷达对目标2以及目标3进行观测，得到尺寸数据如表6所示。

表6 不同雷达尺寸识别结果

由表6可以看出，对于长轴可以通过处理多雷达观测站多圈数据，结果取大值的方法获取三轴稳定卫星的长轴尺寸，精度可达98.8%。对于短轴，目标2(目标本体长宽相差很大)，与标准椭球体形状相差较大，利用椭球体模型得出的轴比不准确，导致短轴估计出现误差；目标3这种类似标准椭球体的目标短轴精度较高，可达88%，随着雷达观察角度的变化，精度还会提升。由于空间目标形状简单，极个别目标为目标2这个形状，所以本文方法可以对空间目标进行尺寸估计。

4 结束语

本文建立了以STK姿态动力学模块与RCS计算程序为核心空间目标动态RCS序列生成方法，可大量、准确和简便地生成RCS仿真数据。建立了空间目标尺寸识别模型，通过仿真数据验证，本模型可识别出空间目标长、短轴尺寸，其中长轴尺寸估计精确，表明本文划定的门限准确。所获得的成果可用于对RCS序列的研究以及对空间目标分类与识别，有利于进一步确定目标属性，提高态势感知能力。