基于修正割线条件的NDL方法

张 翔

(重庆师范大学 数学科学学院，重庆 401331)

考虑无约束优化问题

minf(x),x∈Rn

(1)

其中f:Rn→R连续可微函数.

共轭梯度法一般都具有如下迭代格式

xk+1=xk+αkdk，

(2)

其中αk为通过线搜索获得的步长，dk为搜索方向，一般迭代格式如下：

(3)

其中βk为共轭梯度参数.

步长因子αk一般通过线搜索准则获得，常见的线搜索有强Wolfe线搜索：

|g(xk+αkdk)Tdk|

(4)

f(xk+αkdk)-f(xk)

(5)

其中0<δ<σ<1.gk=f(x)为梯度函数.

Wolfe线搜索：

(6)

f(xk+αkdk)-f(xk)

(7)

其中0<δ<σ<1.gk=f(x)是梯度函数.

经典的共轭梯度法有FR[1]方法，HS[2]方法，PRP[3]方法，LS[4]方法.其参数有如下形式：

其中，‖·‖是欧几里得范数，yk-1=gk-gk-1.

在文献[5]中，Dai和Liao提出了一种DL方法，其参数如下形式：

(8)

其中t≥0，当t=0时，则DL方法退化为HS方法.

在文献[6]中，Hager和Zhang提出了新的

(9)

(10)

在文献[7]中，Dai和Kou提出了一族新的共轭梯度法，其中参数βk如下：

(11)

此外，KOU在文献[8]中提出了一个修正的割线条件：

(12)

(13)

基于以上文献启发，笔者提出一个新的共轭梯度方法，其中的βk形式如下：

(14)

基于修正的割线条件(12)，对于原有的修正割线条件做出修正，提出一个新的共轭梯度参数βk为：

(15)

1 NDL方法的充分下降性

在此，为了后面研究该方法的收敛性，对于目标函数做出如下的两个假设：

(A)水平集Γ={x∈Rn|f(x)f(x0)}有界，其中的x0为起始点，即存在这样的常数k>0使得

‖x‖k,∀x∈Γ

(16)

(B)f在水平集Γ的某个邻域N内连续可微，且其梯度g满足Lipschitz连续，即存在常数L使得

‖g(x)-g(y)‖L‖x-y‖,∀x,y∈N

(17)

‖g(x)‖∀x∈Γ

(18)

定理1 迭代格式为(2)、(3)并且参数βk为NDL方法所示的共轭梯度方法，步长αk满足Wolfe线搜索条件(6)、(7)，则方法NDL能够满足下列的充分下降条件：

(19)

其中c>0.

证对于NDL方法，由文献[9]，可得出NDL方法满足充分下降性条件：

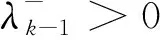
2 NDL方法的全局收敛性

引理1[5]若假设(A)和(B)成立，考虑形如式(2)、(3)、(15)的共轭梯度法，其中dk是充分下降方向，步长αk满足强Wolfe条件(4)、(5)，若

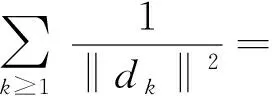
(20)

则该方法具有全局收敛性，即有

(21)

成立.

定理2 若假设(A)和(B)成立，考虑迭代格式为(2)、(3)的共轭梯度法，其中的搜索方向dk是由如下形式的参数βk计算得到

其中dk是下降方向，步长αk满足强Wolfe线搜索(4)、(5)则该方法收敛，即式(21)成立.

(22)

其中c1为大于0的常数，此外，由假设(B)可知

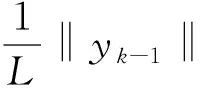
(23)

由式(15)和中值定理可得

|θk-1|=6(fk-1-fk-1)+3(gk-1+gk)Tsk-1

=6g(ηk-1)T(xk-1-xk)+3(gk-1+gk)Tsk-1

=3(gk-1-gηk-1+gk-gηk-1)Tsk-1.

其中ηk-1=τxk-1+(1-τ)xk，并且τ∈(0,1).

由式(17)可得

|θk-1|=3(gk-1-gηk-1+gk-gηk-1)Tsk-1

3(‖gk-1-gηk-1‖+‖gk-gηk-1‖)‖sk-1‖

3(L‖xk-1-ηk-1‖+L‖xk-ηk-1‖)‖sk-1‖=

3(L(1-τ)‖xk-1-xk‖+Lτ‖xk-xk-1‖)‖sk-1‖=3L‖sk-1‖2.

由上式可得

(24)

其中0

由(24)则可知存在常数c2>0使得下式成立

‖zk-1‖c2‖sk-1‖

(25)

由式(15)、(22)和(25)可得

(26)

由式(3)、(15)、(22)、(25)和(26)可得：

‖dk‖=‖-gk+βkdk-1‖

3 结论

结合DL方法，修正的DL方法以及修正割线条件提出一个新的修正NDL方法，并且在一定条件下证明了全局收敛性.在以后研究工作中，可以考虑更加有效的修正方法去修正；所涉及到的方法也含有参数，后面会根据理论结果选取更优的参数.