基于Mathematica的杨氏双缝干涉实验仿真
王高亮,孟 明,王 强
(周口师范学院 物理与电信工程学院,河南 周口 466001)
1690年,荷兰物理学家惠更斯在《论光》一书中,提出了惠更斯原理:波阵面上每一点都可以看作是发射子波的波源,各自发出球面子波,其后任意时刻,这些子波的包迹就是新的波阵面,惠更斯发展了光的波动学说[1]. 1802年,英国的托马斯•杨在研究人眼对颜色视觉效应时,他想出了一个巧妙的方法,演示了光的干涉现象,进一步为光的波动性提供了坚实的实验基础[2]. 杨氏双缝干涉实验是大学物理光学实验中的重要实验之一,在科学研究和工程技术上有着广泛的应用. 以往大学物理课本中,只给出了原理,及形成的一系列的平行等间距的明暗相间的干涉条纹,并指出中央明纹最亮,其他级次的条纹亮度逐级减小,这给学生们的理解产生了很大的困惑[3-4]. 并且传统的杨氏双缝实验对实验条件、设备和场地等有特别的要求,必须在专业的实验室内进行,而有部分院校缺少实验仪器等等[5]. 根据杨氏双缝干涉的理论基础,利用Mathematica为计算工具,对杨氏双缝现象进行仿真,建立了基于计算机系统的模型,在脱离了实验环境和实验设备的约束下,引导读者通过物理计算,进行杨氏双缝干涉的虚拟实验,深化学生对杨氏双缝实验的理解,达到更好地掌握大学物理内容的目的,对大学物理教育有非常重要的意义.
1 杨氏双缝实验原理

图1 杨氏双缝实验原理图
杨氏双缝干涉实验原理如图1所示,其中小孔S发出球面波,可视为点光源,狭缝S1,S2到S的距离相等. 根据惠更斯原理,如果狭缝S1,S2所处位置是球面波的波阵面,则S1,S2可看成发射子波的新波源,其产生的波在空间相遇,因满足频率相同、振动方向相同、位相差恒定的相干条件,则在波场会产生干涉现象,这种方法称为分波阵面法获得相干光. 由于激光的产生,利用其良好的单色性,代替原来的普通光源,在重叠区域会产生干涉现象,便可在干涉屏上观察到明暗相间的干涉条纹,在干涉场通过光与物质的作用,曝光、显影之后就可以在合适的感光材料上记录全息图样,从而可以制作一维光子晶体[6-8].
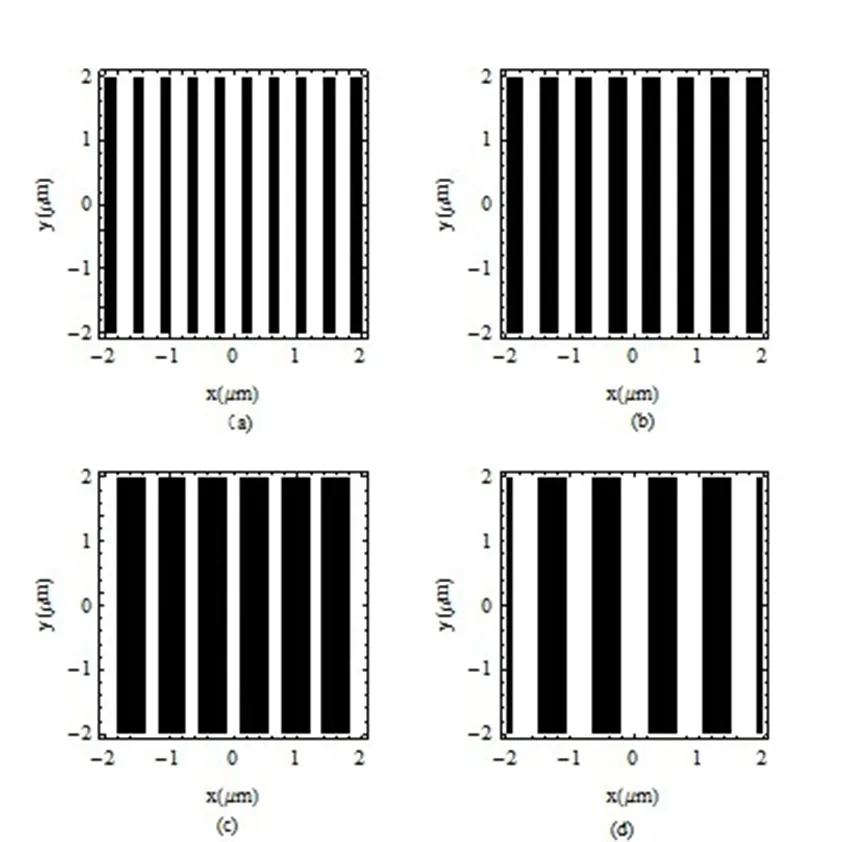
根据原理图,可以对干涉条纹的位置、间距做定量分析. 如图1所示,双缝S1,S2的间距为d,缝到干涉屏之间的距离为D,一般情况下d< (1) 则P点的光强决定于从S1,S2发出的两束光的相位差,决定于光程差,也就是决定于两束光的光程差δ. 相位差 (2) 由于分波面法,两列相干波的初相相同,则有: (3) 干涉加强或减弱的条件 (4) k=0,±1,±2,±3,...,其中k为级次,明纹位置 (5) k=0,±1,±2,±3,...,从中可以看出,k=0,称为中央明纹或零级明纹,干涉条纹的级次k越大,x越大,离中央明纹越远. (6) k=0,±1,±2,±3,... 暗纹位置 (7) k=0,±1,±2,±3,... 其他都是界于最明和最暗之间. 相邻的两明(暗)条纹的距离为 (8) 说明,当θ不太大时,干涉场是一系列的平行等间距的明暗相间的条纹,条纹是等间距分布的. 杨氏双缝实验在实际的应用中,可以测量入射光的波长. 由式(5)可得 (9) 或根据式(8),可以得到 (10) Clear[t] %首先清除变量 λ=0.532; %设定波长 z=100;%观察点,即干涉场点 a=125; r1=z+((x+a/2)2+y2)/(2z);%S1到P点的光程 r2=z+((x-a/2)2+y2)/(2z);%S1到P点的光程 t=Abs[u1+u2];%P点光强 ContourPlot[t2,{x,-2,2},{y,-2,2},ContourLines→False,Frame→True,PlotRange→{Automatic,0.00014},ColorFunction©Black,FrameLabel→{"x(mm)","y(mm)"," ",""}] %仿真画出P点光强的等高图. 根据式(5)、(7)、(8),可以在实验中设定入射光的波长λ,双缝S1,S2的间距为d,缝到干涉屏之间的距离为D的值,进一步观察影响干涉条纹明(暗)纹位置、明(暗)纹间距的因素. 当d,D一定时,同过改变入射光的波长,可以得到不同的干涉条纹. 模拟的结果如图2所示,双缝的间距d为10 μm,D为100 μm时的干涉图样,从图中可以看出是一组平行的明暗相间的直条纹. 图2(a)是入射光的波长为390 nm,形成的干涉条纹周期为422 nm,达到了光波长量级,可以看作是一维的光子晶体;图2(b)是入射光的波长为532 nm,周期变化不大,但是明纹的宽度有了明显的加宽;图2(c)是入射光的波长为690 nm,其周期为542 nm;图2(d)是入射光的波长为760 nm,其周期为600 nm. 从这几幅图中,可以看到,随着光波长的增加,周期也在增加,即明暗条纹的间距也在增加,验证了公式(8)的正确性. 当入射光的光波长λ和双缝的间距d一定时,同过改变缝和屏的间距,可以得到光栅常数不同的干涉条纹. 模拟的结果如图3所示,入射波长λ=532 nm,d为10 μm时的干涉图样. 图2 改变波长λ形成的干涉图 图3 改变D形成的干涉图 图3(a)是D=100 μm时的干涉图样,从图中可以看到周期为0.420 μm;(b)是D=125 μm时的干涉图样,从图中可以看到周期增大,变为0.615 μm;(c)是D=150 μm时的干涉图样,从图中可以看到明纹增宽,周期为0.667 μm;(d)是D=200 μm时的干涉图样,从图中可以看到周期为0.889 μm. 按照实验原理搭建光路,用波长为532 nm的半导体激光器和波长为632 nm的氦氖激光器代替普通光源,在干涉场通过显微镜观察干涉图案,并用照相机或记录介质记录干涉图结构[9-13]. 如图4所示,可以清楚地看到平行直条纹的干涉图样,与图2、图3的理论计算结果吻合的非常好. 运用Mathematica理论计算了杨氏双缝干涉光场的干涉图样,搭建了实验光路,记录了全息干涉图,实验观察结果与理论模拟很好的吻合. 通过改变影响明纹位置、明纹间距因素的参数波长λ和缝到屏的间距D,得到了周期不同、光栅常数不同的干涉图样. 论文的创新之处,运用Mathematica理论计算杨氏双缝干涉实验,特别是对实验条件达不到的院校,也可以使学生加深对实验现象,实验规律和实验原理的掌握,仿真模型极大地节约了实验成本,实现资源共享. 此外,运用激光干涉,也可以大规模地制作波长量级的一维光子晶体. 图4 不同放大倍数的干涉图样2 仿真程序的编写

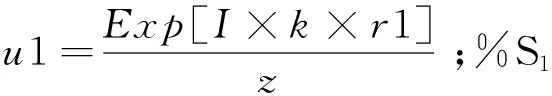

3 仿真结果及波长、D对干涉条纹的影响
3.1 波长对干涉条纹的影响
3.2 改变D对干涉的影响

4 实验结果分析
5 结论


