基于弯矩最小化的地铁盾构隧道横断面优化设计分析

黄大维， 冯青松， 刘开富， 张鹏飞， 唐柏赞, 涂文博

( 1. 华东交通大学 铁路环境振动与噪声教育部工程研究中心， 江西 南昌 330013；2. 浙江理工大学 建工学院， 浙江 杭州 310018)

现有的盾构隧道横断面普遍采用圆形，为了合理地利用横断面空间或提高施工效率，也有采用其他形状的盾构隧道横断面，如横椭圆形、矩形、类矩形(宁波地铁三号线采用)、半圆形、马蹄形、双圆形、三圆形等。作为地下结构的盾构隧道承受的主要荷载为土压力，正常情况下，隧道承受的竖向土压力要大于水平土压力，导致盾构隧道发生横椭圆变形。文献[1]规定，盾构隧道施工验收时最大的椭圆度变形为5D‰(D为隧道的直径)，对于某些地层条件，难以达到该规范要求。此外，软土地层的水平地层抗力系数小，隧道变形过程中其水平地层抗力的增量非常有限。因此，软土地区盾构隧道更容易发生横椭圆变形超限[2-4]，从有据可查的资料分析看，我国不少软土地区的盾构隧道出现了横椭圆变形超限。

从平面应变角度看，盾构隧道可视为曲梁结构，且曲梁长度远大于曲梁高度，由结构力学可知，梁结构发生变形主要由弯矩所致[5-6]。文献[7]研究表明，盾构隧道发生横断面变形，绝大部分是由于弯矩作用下管片纵缝接头发生转动所致(其他部分是由管片弯曲所致)。盾构隧道的横断面在过大弯矩作用下，管片纵缝接头位置易发生管片棱角破损，防水密封垫间压应力减小，甚至防水密封垫间完全张开而导致接头防水失效[8-9]，连接螺栓的螺纹发生塑性变形而导致管片纵缝接头破损[10-11]。由此可见，管片纵缝接头的病害绝大部分是由盾构隧道横断面的弯矩过大所导致。为了减小管片纵缝接头的弯矩，文献[12]建议管片环分块时尽量将纵缝接头设计在弯矩较小的位置，但为了施工的可操作性，管片环必须有一定分块数量，将不可避免地导致部分管片纵缝接头位于弯矩较大的位置。

若能设计出一种盾构隧道横断面，使其在围岩压力作用下任意截面的弯矩均为0(在此称之为“零弯矩盾构隧道横断面”)，上述的盾构隧道病害则可避免，也可以减少管片配筋。但在实际中，一条或多条地铁线路的盾构隧道只能选用一种横断面形式，因此，只能综合评估整条地铁线路中盾构隧道全部横断面的围岩压力，最终以某一横断面形状作为该地铁线路的盾构隧道横断面。本文提出了零弯矩盾构隧道横断面设计理念，给出零弯矩盾构隧道横断的结构力学模型及横断面轴线的计算方法，并对零弯矩盾构隧道横断面特性与影响因素进行了分析。最后提出了基于弯矩最小化的盾构隧道横断面设计方法，并对其合理性进行了论证分析。研究成果可为盾构隧道结构设计提供参考与借鉴。

1 零弯矩盾构隧道横断面分析

1.1 盾构隧道周围土压力假设

零弯矩盾构隧道横断面轴线(此时轴线上任意截面弯矩均为0)设计时，为方便分析计算，在此先考虑最一般情况，对盾构隧道承受的荷载做如下假设：

(1) 无水平地层抗力

因所设计的盾构隧道横断面无弯矩，隧道的水平变形很小(横断面变形主要由弯矩所致)，甚至可以忽略不计，因此，隧道侧部的水平抗力也可以忽略不计。

(2) 不考虑盾构隧道结构自重

盾构隧道自重比其所受到的周围土压力要小得多。如文献[1]规定，衬砌厚度宜为隧道外径的0.04～0.06倍，而上覆土厚度远大于管片厚度，因此，隧道自重导致隧道结构产生的弯矩要远小于周围土压力导致隧道结构产生的弯矩。为了方便计算，在此不考虑盾构隧道结构自重，作为工程问题进行适当简化是合理可行的。

(3) 隧道的竖向土压力按土柱理论计算，地层符合水土合算(即假设隧道位于软土地层中)。对于需要考虑土拱效应的地层及应采用水土分算的地层，后面再补充说明，在此以最一般的情况进行理论分析。

根据上述理论假设，得到盾构隧道周围土压力，见图1。

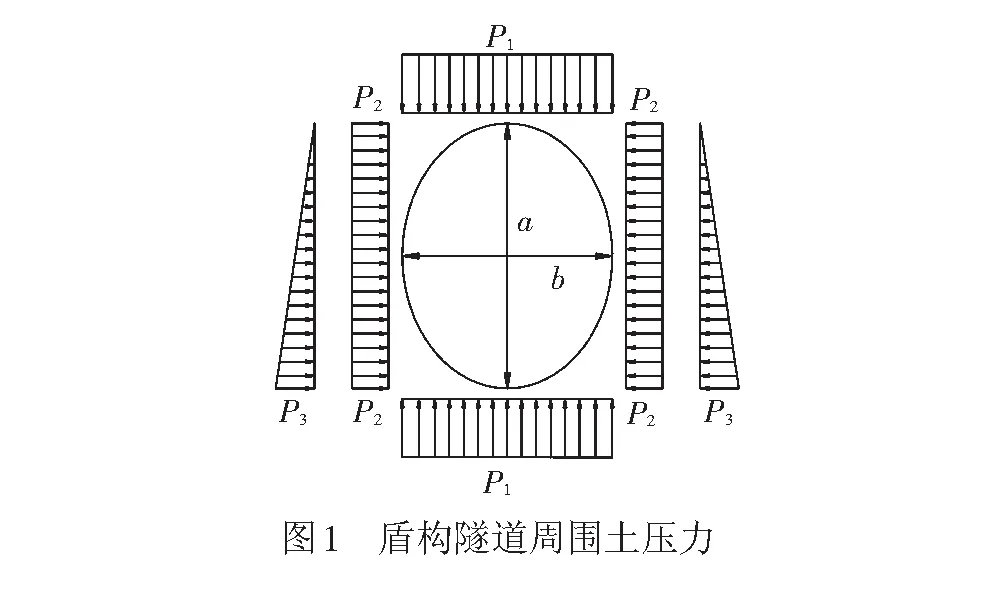
图1中的土压力计算为

P1=γH

( 1 )

P2=γHk=P1k

( 2 )

P3=γak

( 3 )

式中：a为盾构隧道的竖直径；b为盾构隧道的中心水平直径(即在竖直径中心位置的水平直径)；P1为竖向土压力；P2为隧道顶部位置的水平土压力；P3为隧道顶部与底部的水平土压力之差；γ为地层中土体的容重，对于土层分层情况下，则取为平均容重；H为隧道上覆土层厚度；k为隧道穿越土层的侧土压力系数。

1.2 盾构隧道受力分析

盾构隧道在土压力作用下，取单位长度进行分析，隧道结构简化为曲梁结构，简化后的土压力单位为线荷载单位(kN/m)，其数值与三维状态下的土压力数值相同(三维状态下土压力单位为kN/m2，即为kPa)。由图1可知，盾构隧道为对称结构且荷载为对称荷载，因此只需要分析一半即可，对应的结构力学模型见图2。由结构与荷载的对称关系及∑X=0可知，截面A、B处的剪力Q1与Q2均为0。在此需要计算出盾构隧道横断面截面零弯矩的轴线方程，假设截面A、B的弯矩均为0，可得到盾构隧道横断面合理轴线的结构力学计算模型，见图3。

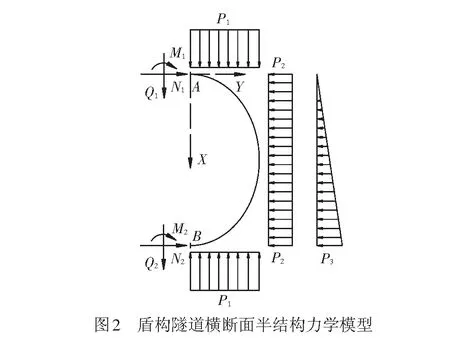
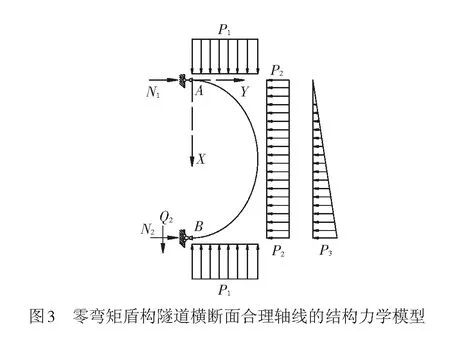
由∑MA=0，∑Y=0，可得

( 4 )

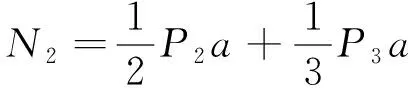
( 5 )

1.3 零弯矩隧道横断面轴线计算

设图3中盾构隧道上半部分任意截面S的坐标为(x，y)，见图4。截面S的弯矩为

( 6 )

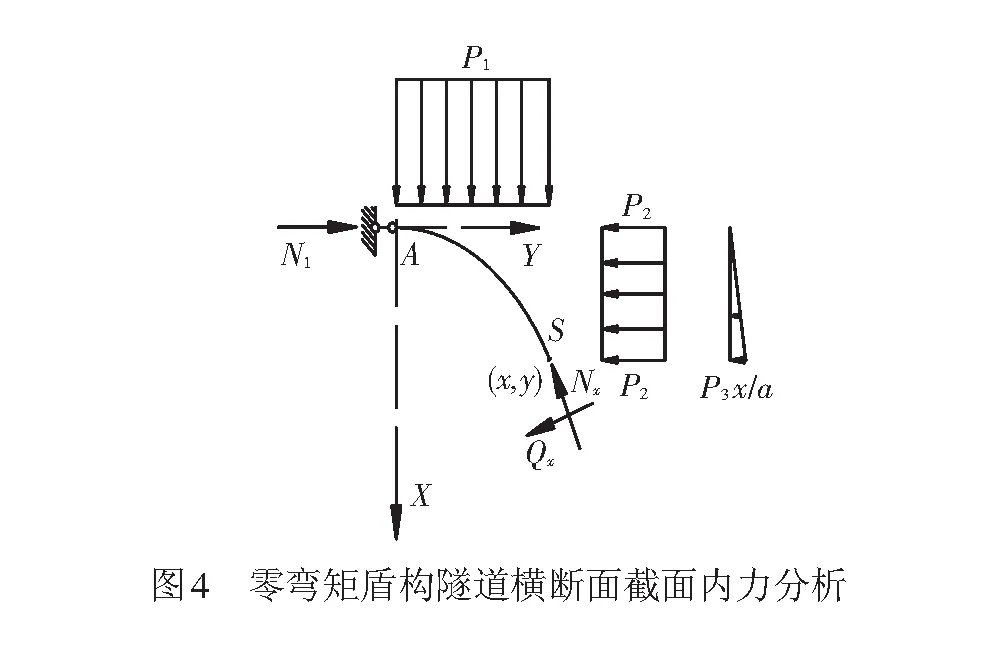
由式( 6 )可见，截面S的弯矩MS前三项均为水平荷载所导致的弯矩，其大小只与x有关；后一项为竖向的荷载所导致的弯矩，其大小只与y有关。前三项的弯矩与对应的简支梁在受到相同的水平荷载作用下的弯矩表达式相同，见图5。简支梁在坐标x位置处的弯矩表达式为

( 7 )

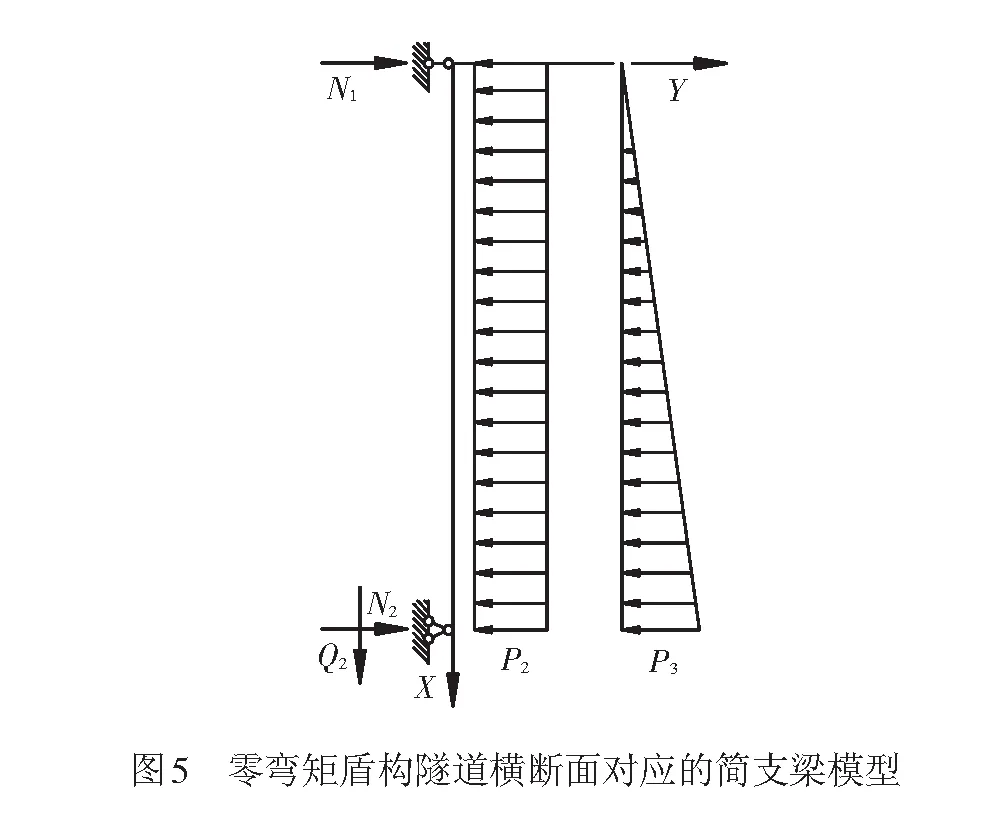
若需要使截面S满足弯矩为0，则截面S的y坐标表达式为

( 8 )

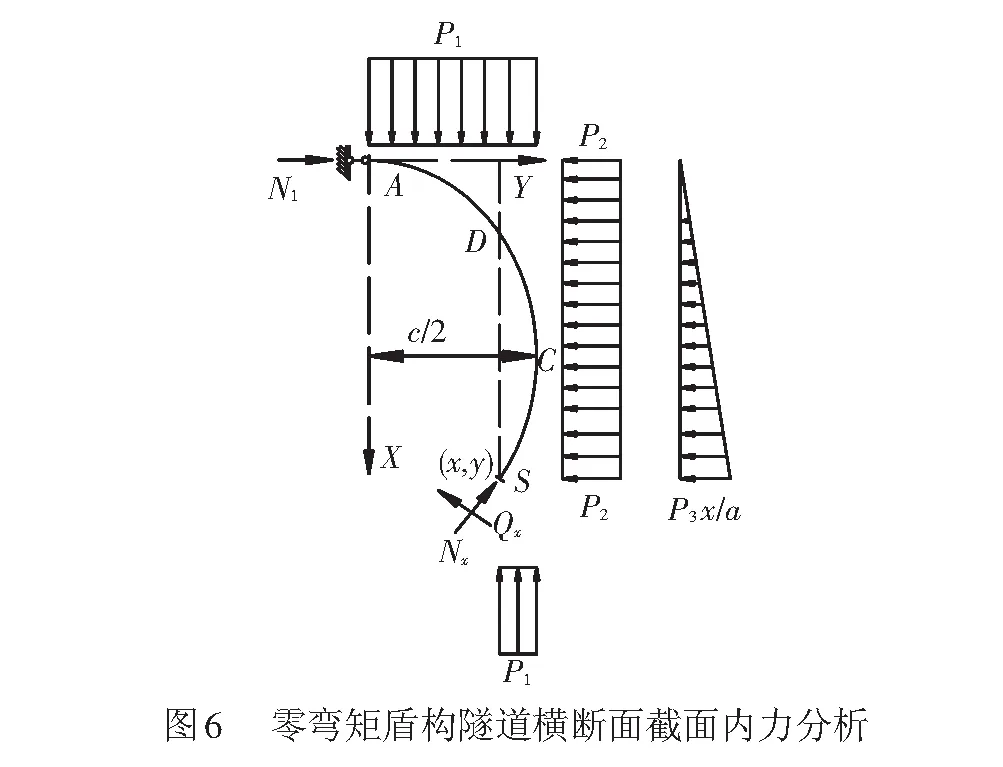
然而，当截面S位于隧道下半部分时，隧道底部的竖向荷载对截面S也产生弯矩，见图6。但是图6中隧道下部的竖向荷载对曲线CS作用导致截面S产生的弯矩，与图6中隧道上部的竖向荷载对曲线DC作用导致截面S产生的弯矩大小相等，方向相反，即相互抵消。因此，式( 8 )可适用于图3中的任意截面。

1.4 零弯矩盾构隧道水平直径计算

由盾构隧道横断面合理轴线计算公式及对应的简支梁弯矩计算公式可知，因盾构隧道的侧土压力为上小下大，导致盾构隧道的最大水平直径并不是出现在竖直径中心位置，而是要比竖直径中心位置偏低，在此将盾构隧道的最大水平直径用c表示(a、b、c均为隧道横断面轴线的直径，而非外径)。

当x=a/2时，对应的y为b/2，根据式( 8 )可得到b的计算式为

( 9 )

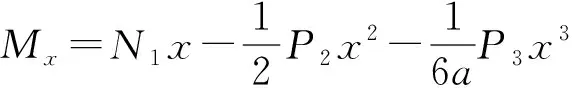
(10)

由图5可知，x∈[0,a]利用当β=0时所对应的x代入式( 7 )，计算得到的Mx值最大。因此，由β=0时所对应的x值计算得到的y值也最大。当β=0时所对应的x值为

(11)

(12)

以最大水平直径与中心水平直径竖向距离作为偏心距Δo，则其计算式为

(13)

1.5 零弯矩盾构隧道的横断面特性分析

假设地层土体容重γ为20 kN/m3，隧道的竖向土压力按土柱理论计算，得到不同隧道上覆土厚度H与不同侧土压力系数k时，竖直径a分别为6、15 m的零弯矩盾构隧道横断面的关键参数，见表1～表4。

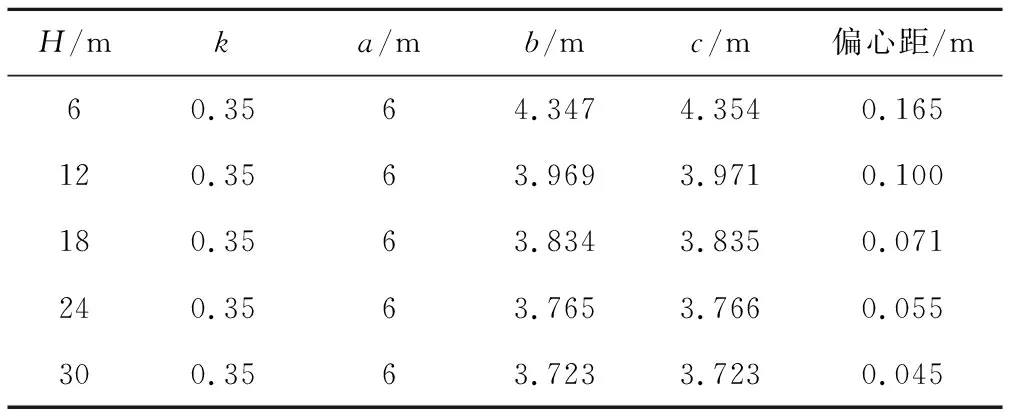
表1 竖直径为6 m时不同埋深的零弯矩隧道关键参数

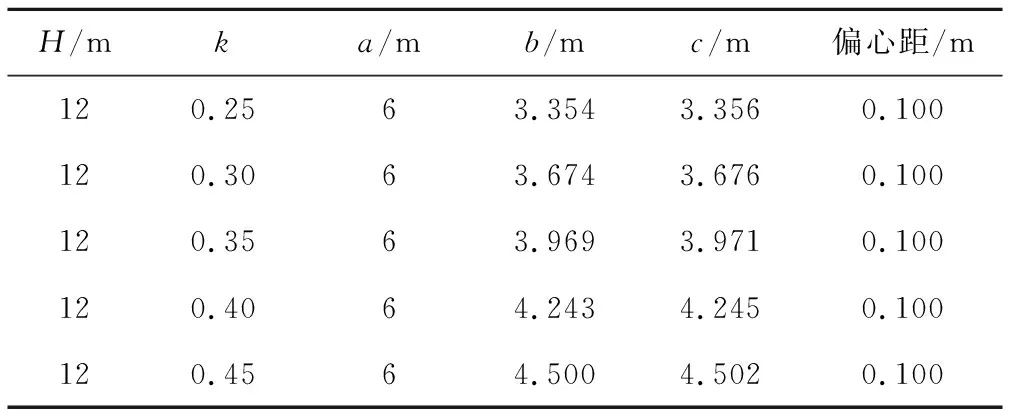
表2 竖直径为6 m时不同侧土压力系数的零弯矩隧道关键参数

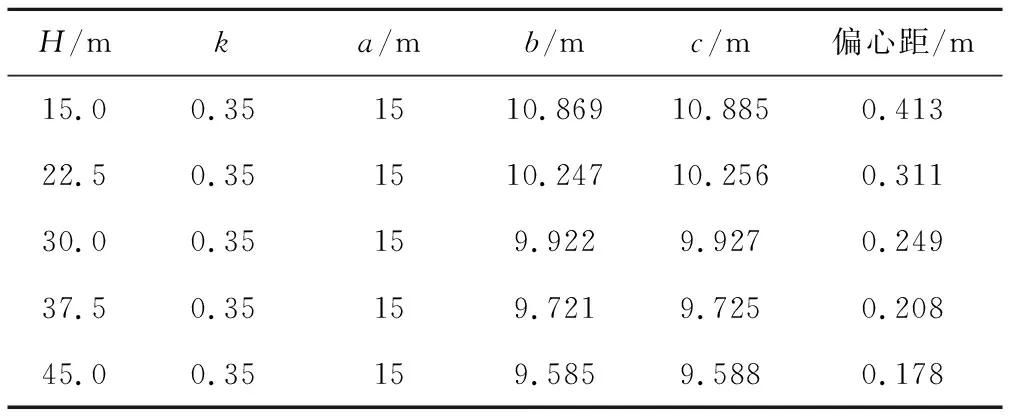
表3 竖直径为15 m时不同埋深的零弯矩隧道关键参数

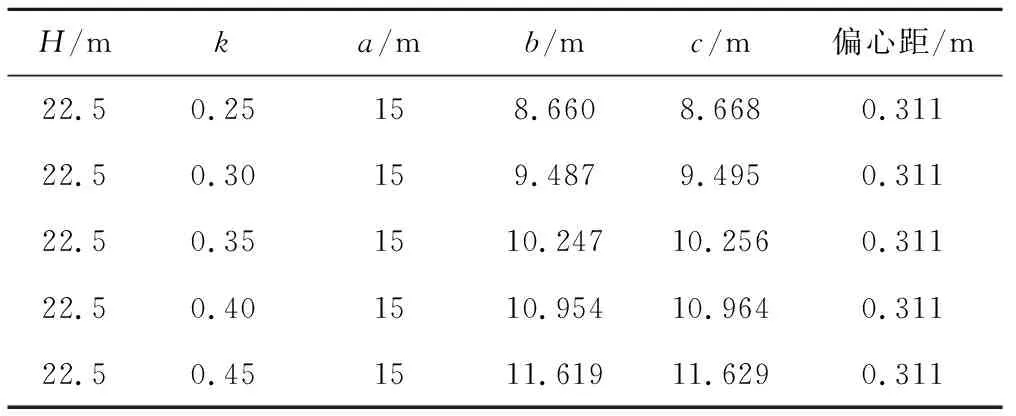
表4 竖直径为15 m时不同侧土压力系数的零弯矩隧道关键参数

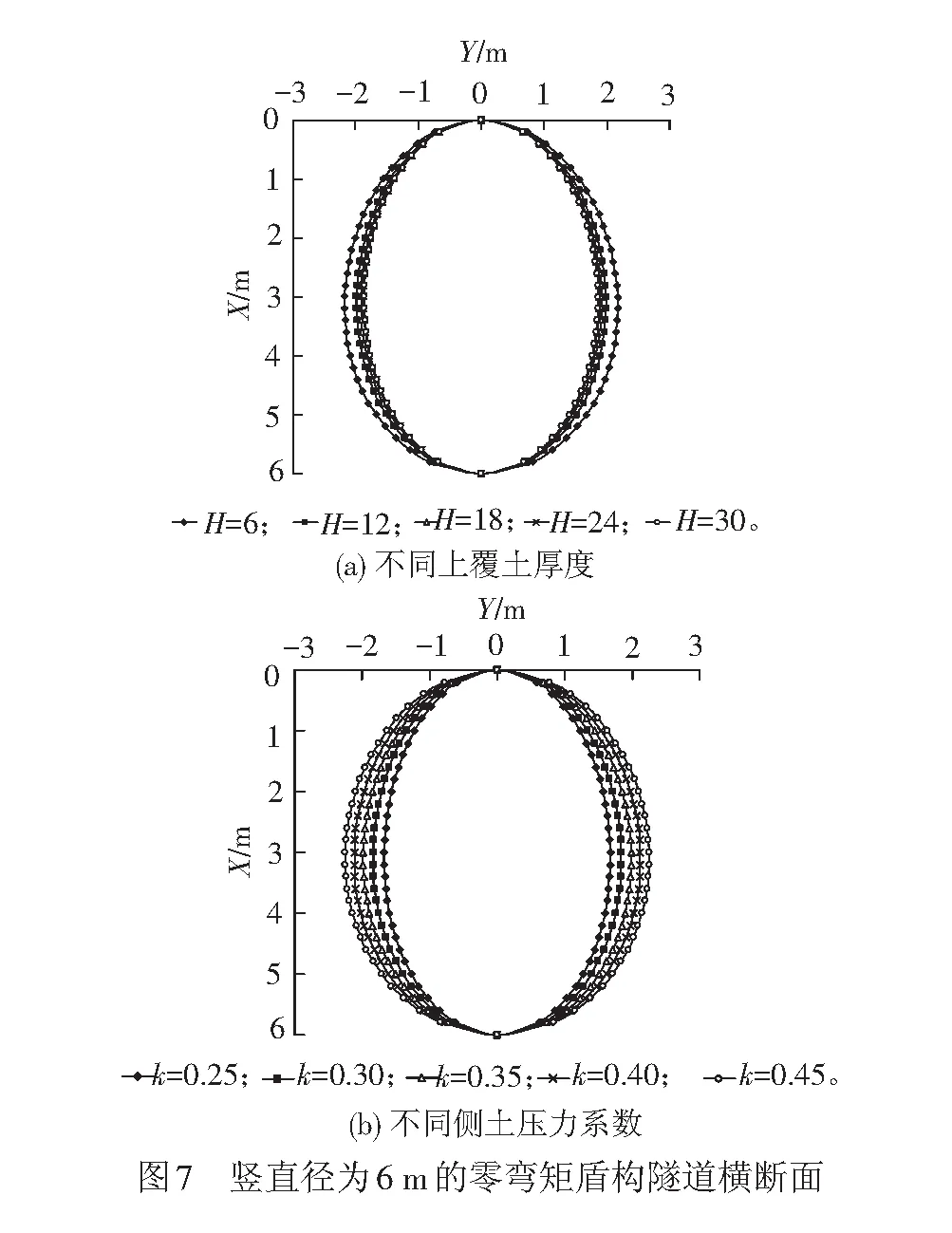
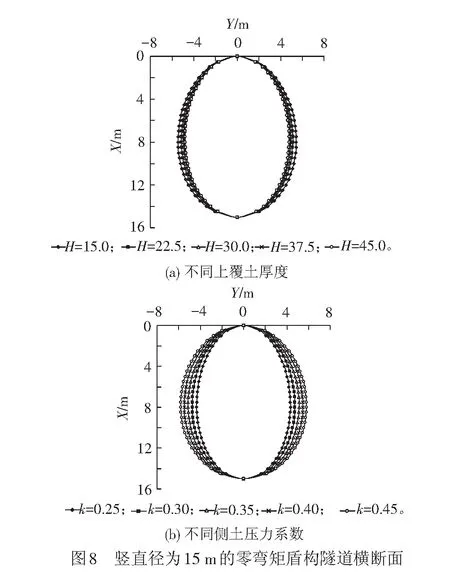
由表1～表4可以看出，零弯矩盾构隧道的中心水平直径b与最大水平直径c均小于竖直径a。由表1与表3可以看出，隧道上覆土层厚度越大，偏心距Δo越小，中心水平直径b与最大水平直径c也越小。由表2与表4可以看出，随着侧土压力系数k的增大，零弯矩盾构隧道的偏心距Δo不变，中心水平直径b与最大水平直径c均增大。

考虑到横断面轴线计算式与表1～表4均无法直观地看出零弯矩盾构隧道的横断面，为此，将表1～表4的零弯矩盾构隧道的横断面作图，见图7、图8。由图7与图8可见，相对隧道上覆土厚度，侧土压力系数k对零弯矩盾构隧道的横断面形状影响相对显著。

2 基于弯矩最小化盾构隧道横断面优化设计

由零弯矩盾构隧道横断面轴线的公式推导可知，横断面轴线表达式与隧道周围土压力有关。然而，在实际应用中，一条或多条地铁线路所采用的盾构隧道横断面必须相同，以方便经济合理地利用盾构机，也方便管片厂预制管片等。而一条或多条地铁线路的盾构隧道埋深、隧道上覆土层、穿越土层的力学性能均有变化[13]。因此，在盾构隧道横断面形状设计时，需要合理地评估影响隧道周围土压力的相关参数，如隧道的埋深、隧道穿越土层的侧土压力系数等，在综合权衡后确定盾构隧道横断面设计的土压力模式，并以此土压力模式所确定的零弯矩盾构隧道横断面作为所考虑范围内的盾构隧道横断面。

为此，提出加权平均法确定盾构隧道横断面设计的土压力模式。如在确定横断面设计的竖向土压力P1时，将所考虑的地下线路范围内隧道的竖向土压力分为若干区段，分别为P1-1，P1-2，P1-3，…，P1-n，对应的盾构隧道长度分别为Lp-1，Lp-2，Lp-3，…，Lp-n，盾构隧道总长度为L。则盾构隧道横断面设计土压力模式的P1取值计算式为

P1=

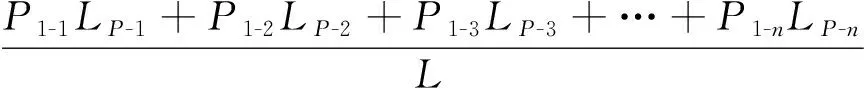
(14)

同理，对于盾构隧道的侧土压力系数k，也采用上述同样的方法进行加权平均取值，即将所考虑的地下线路范围内隧道的侧土压力系数分为若干区段，分别为k1，k2，k3，…，kn，对应的盾构隧道长度分别为Lk-1，Lk-2，Lk-3，…，Lk-n，盾构隧道总长度为L。则盾构隧道横断面设计土压力模式中的侧土压力系数k取值计算式为

(15)

其他设计参数均可采用类似的加权平均法进行取值。对于盾构隧道穿越土层为多层的情况下，侧土压力系数取值参照文献[14]的建议，即将盾构隧道穿越土层的各层土的侧土压力系数进行加权平均。

基于零弯矩盾构隧道设计理论，并利用加权平均法评估盾构隧道横断面设计的土压力计算参数，进而得到一条或多条地铁线路所采用的盾构隧道横断面。由此可见，基于弯矩最小化得到的盾构隧道横断面，在绝大多数情况下，盾构隧道横断面在理论上均不是零弯矩，而采用此方法的目的是最大限度地减小全线盾构隧道的弯矩。

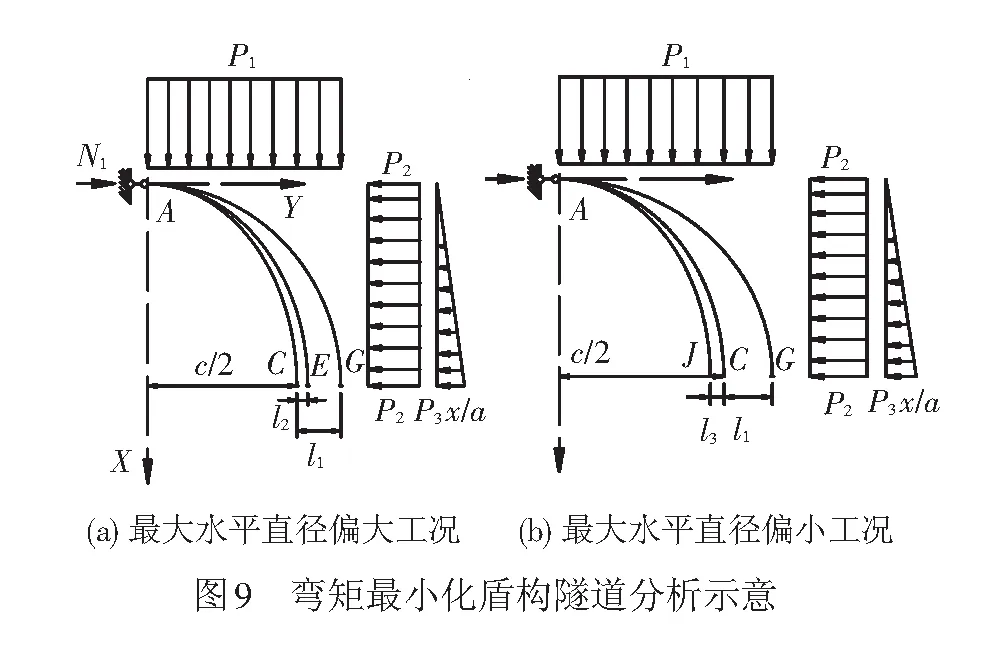
为了论证说明，假设由加权平均法所得到的零弯矩盾构隧道横断面(在此也称之为“设计隧道横断面”)作为某地铁线路的盾构隧道横断面时，当某地层条件下的零弯矩盾构隧道的最大水平直径大于设计隧道横断面的最大水平直径时，见图9(a)(曲线AC为设计隧道横断面半结构的上部分，根据图6得到；曲线AE为某地层状态的零弯径盾构隧道横断面半结构的上部分；曲线AG为圆形盾构隧道横断面半结构的上部分)。因图9(a)中l1大于l2，由式( 6 )可知，E截面的弯矩显然要小于G截面的弯矩。同理，当某地层条件下的零弯矩盾构隧道横断面的最大水平直径小于设计隧道横断面最大水平直径时，见图9(b)(曲线AJ为某地层状态的零弯矩盾构隧道横断面半结构的上部分，其他与图9(a)同)，因图中l1大于l3，由式( 6 )可知，J截面的弯矩显然要小于G截面的弯矩。结合图7与图8可知，尽管在分析零弯矩隧道特性时选取的侧土压力系数变化范围较大，但表1～表4所示的任意工况下零弯矩盾构隧道的横断面均与圆形横断面相差较大，且同一竖直径的零弯矩盾构隧道，在任意工况下最大水平直径c之间的差值(对于表2，c之间的最大差值为1.146 m)，均要小于任意工况下最大水平直径与对应同竖直径圆形隧道直径之间的差值(即c与a的差值，对于表2，c与a的最小差值为1.498 m)。当采用加权平均法设计参数时，最终确定的设计隧道横断面最大水平直径c为各工况下零弯矩盾构隧道横断面最大水平直径c的近似加权平均，设计隧道横断面最大水平直径c与全线各地层条件下的零弯矩盾构隧道横断面最大水平直径间较小。由此可见，虽然在实际应用时设计隧道的横断面弯矩并不为0，但相比圆形横断面，其弯矩有了大幅度地减小。如赵州桥，其拱形轴线并不是在任何情况下弯矩均为0，而是在设计时根据其设计的主要荷载(如拱桥自重荷载、车辆荷载等)综合考虑确定其拱轴线在各工况下的弯矩比其他形状的拱轴线的弯矩要小，所以赵州桥经久耐用。

为了方便应用本文提出的基于弯矩最小化的盾构隧道横断面优化设计方法，在此给出设计流程图，见图10。

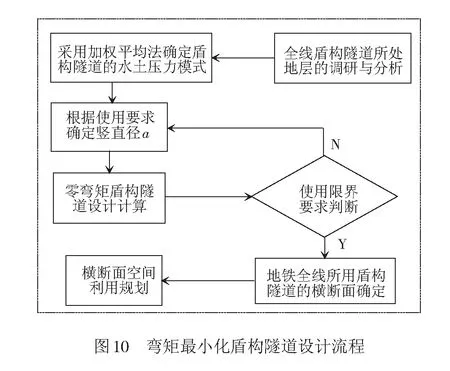
3 隧道横断面设计的土压力模式分析

由以上分析可知，在确定盾构隧道横断面时，需要确定全线各地层条件的盾构隧道土压力模式及其对应的长度。然而，实际中因地层的围岩特性不同，盾构隧道受到的围岩压力也不同。为此分别对松弛土压力及考虑地下水的情况进行分析。

3.1 松弛土压力的情况

当盾构隧道位于自稳能力良好的地层中时，隧道顶部的竖向土压力要小于土柱理论土压力。关于松弛土压力的计算，现在最为普遍的是采用太沙基(Terzaghi)公式计算[15]，其竖向土压力示意见图11(a)。在太沙基计算式中，隧道顶部的竖向土压仍近似地取为均布荷载，且隧道的水平土压力为梯形分布荷载(上小下大)。此外，当隧道埋深较大且地层的自稳能力较好时，隧道的竖向土压力按普罗托雅科诺夫(1990年)提出的深埋隧道衬砌荷载的计算模型[16](见图11(b))，且普氏理论土压力与太沙基土压力一样，即隧道顶部的竖向土压也是近似地取为均布荷载，隧道的水平土压力也是假设为梯形分布荷载(上小下大)。

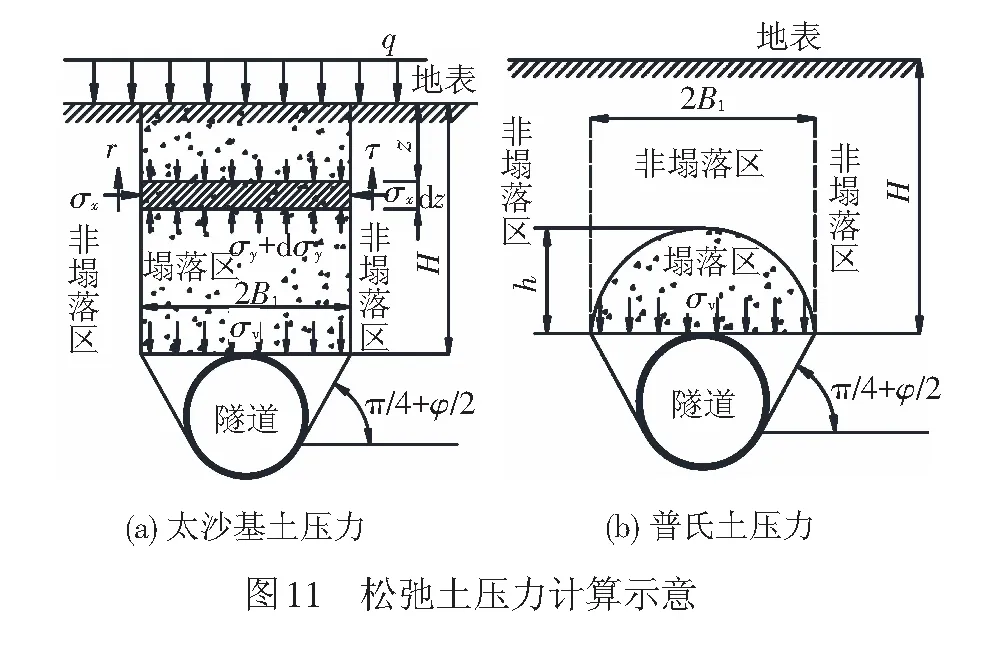
因此，对于考虑松弛土压力的情况，同样可以对应到图1的土压力模式中，即隧道顶部与底部的竖向土压力P1取为松弛土压力理论的隧道顶部土压力，即图11中的σv(因忽略隧道自重对隧道结构内力的影响，隧道底部与顶部的竖向土压力相同)，P2取为隧道的顶部水平土压力，P3取为隧道底部与顶部的水平土压力之差。因所设计的为零弯矩盾构隧道横断面，在围岩压力作用下可忽略隧道变形，所以无需考虑隧道受到的水平地层抗力。

3.2 考虑水压力的情况

在零弯矩盾构隧道公式推导时，未考虑水压力的作用。当盾构隧道位于地下水位以下且地层符合水土分算条件时，为了方便应用本文提出的零弯矩盾构隧道设计理论，建议水压力按水平与垂直水压力分别作用的方式表示(即水压力采用投影表示法)。其中隧道顶部与底部的竖向压力在不考虑水压力基础上进行修正即可。考虑到在地下水压力作用下，盾构隧道将受到上浮力，但在隧道上覆土的竖向土压作用下，隧道并不会发生上浮，即从无地下水到有地下水的过程中，隧道顶部的竖向压力的增量为

ΔP=γwa

(16)

因此，当盾构隧道位于地下水位以下且地层符合水土分算条件时，图1中土压力计算式为

(17)

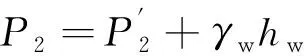
(18)

(19)

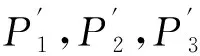
4 结论

(1) 针对盾构隧道在过大的弯矩作用下发生横椭圆变形超限，并由此诱发管片纵缝接头结构病害与防水失效等问题，为了尽量减小盾构隧道横断面截面的弯矩，提出了零弯矩盾构隧道横断面设计理念。

(2) 根据隧道的围岩压力特点及合理假设，得到零弯矩盾构隧道横断面合理轴线的结构力学模型及合理轴线解析表达式，同时给出零弯矩盾构隧道横断面关键参数的计算公式。

(3) 零弯矩盾构隧道横断面呈竖鸭蛋形状，其中心水平直径b与最大水平直径c均小于竖直径a。侧土压力系数k对零弯矩盾构隧道的横断面形状影响相对显著。

(4)基于弯矩最小化盾构隧道横断面设计时，考虑到实际中一条或多条地铁线路所采用的盾构隧道横断面必须相同，提出了加权平均法取值盾构隧道横断面设计的土压力参数。

(5)基于弯矩最小化得到的盾构隧道横断面，在实际中其弯矩均不为零，而采用此方法的目的是最大限度地减小全线盾构隧道的弯矩。分析表明，相比传统的圆形横断面，基于弯矩最小化得到的盾构隧道横断面弯矩有大幅度地减小。