轨道交通列车通过时轨侧广告牌的受力特性*
孟 添 张继业 李 田
(西南交通大学牵引动力国家重点实验室,610031,成都//第一作者,硕士研究生)
关于列车通过时轨侧结构的空气动力学分析,国内外学者做了大量的研究工作。文献[1-5]侧重分析车外轨侧结构挡风墙对列车气动性能和动力学性能的影响,但未涉及到对轨侧结构本身受到的压力和气动力的分析。对轨侧结构压力和气动力分析主要集中在对声屏障的分析。文献[6]在自然横风环境下,对高速列车通过声屏障进行了数值模拟,并通过风洞试验验证了数值模拟的正确性。文献[7]通过对列车通过不同轨侧结构的试验结果进行了分析,分别提出了压力峰值系数公式。文献[8]对声屏障气动特性进行了仿真分析,得到了压力峰值与列车运行速度呈二次函数关系。文献[9]分析声屏障脉动力分布特性及脉动力时程变化特性,定性分析了列车运行速度、声屏障高度、距轨道中心线距离等因素对脉动力的影响规律。文献[10]对列车经过声屏障过程进行仿真,计算结果与国外相关试验结果相吻合。文献[11]对列车通过时路堤声屏障气动力特性进行数值仿真,对声屏障上测点的内外侧压差幅值结果进行分析,并计算了声屏障的结构响应。文献[12]通过列车脉动风载荷公式得到风载荷幅值并计算了防风屏障的结构响应。由于声屏障延伸范围相对较长,上述文献主要针对某些典型位置的压力等进行分析,对表面压力、气动力等具体分布的分析较少。目前,列车通过时轨侧广告牌的气动特性研究未见公开报道。本文主要分析轨侧广告牌表面压力及气动力分布规律,研究了不同列车速度下广告牌所受压力及气动力变化规律。
1 控制方程
当列车在明线轨道上运行时,其马赫数小于0.3,空气可视为不可压缩气体。其周围流场可考虑为三维粘性非定常的湍流流场,湍流模型采用k-ω两方程模型。采用有限体积法对N-S方程及湍流方程进行求解,控制方程的运输方程形式为[4]:
(1)
式中:
t——时间;
ρ——空气密度;
u——流场速度矢量,u=(u,v,w);
ut——列车运动速度矢量,ut=(ut,0,0);
ut——列车运行速度;
φ——流场通量;
S——源项;
Γ——扩散系数。
2 仿真计算模型及网格划分
列车计算模型采用国内某型号地铁列车,考虑了转向架及内风挡等结构,忽略了车体表面凹凸结构、头尾车端部连接装置、车底设备以及转向架上一些复杂结构等。由于列车中部截面变化不大,且流场结构基本稳定[13],因此采用3节编组(如图1所示)。计算区域分为滑移计算区域和固定计算区域两个部分。列车及周围一定范围为滑移区域,包括广告牌在内的外场区域为固定区域(如图2所示)。整个计算区域宽为120 m。广告牌为一平板模型,广告牌内侧距离轨道中心线3.55 m,广告牌宽0.05 m,长35.00 m,高3.50 m。

图1 列车模型
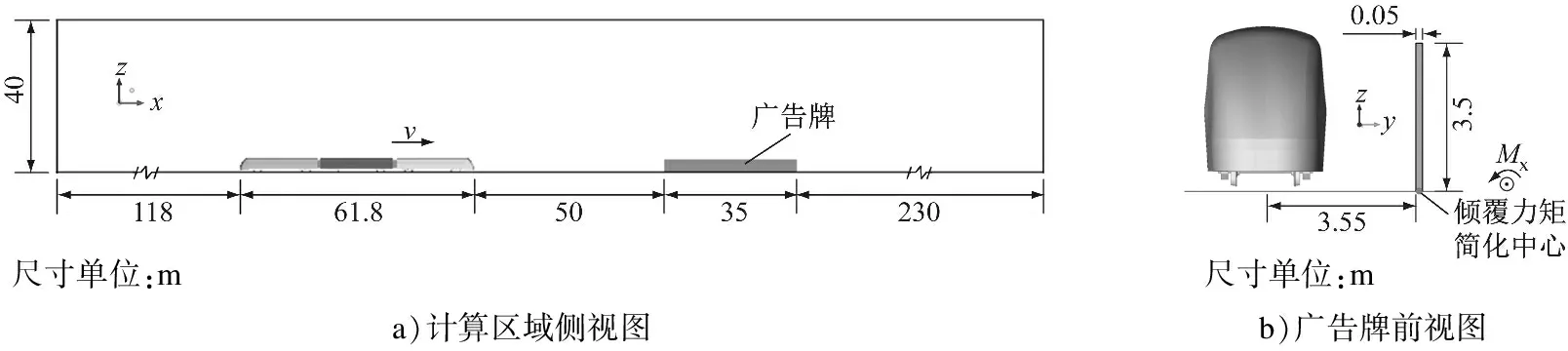
尺寸单位:ma)计算区域侧视图 尺寸单位:mb)广告牌前视图
图2 列车通过广告牌计算区域
列车沿x轴正方向运行为参考方向,固定计算区域的两侧面边界和顶部边界设置为对称边界条件;固定计算区域及滑移区域的两端面边界都设置为压力出口条件,出口压力为0;固定计算区域和滑移计算区域的底面设置为无滑移壁面;固定计算区域的内侧面和滑移计算区域的外侧面设置为interface面;滑移计算区域的速度设置为列车运行速度。
对广告牌作分块处理(如图3)以分析其受力情况。广告牌分为5个小区域和4个大区域,两种区域分别长3 m和5 m。每个小区域从上往下分为相同大小的5个监测块,每个监测块取其几何中心的纵向和竖向坐标表示其位置,在每个监测块的中心位置布置1个压力监测点;每个大区域中间从上往下间隔布置3个压力监测点,分别位于3.15 m、1.75 m和0.35 m高度。广告牌倾覆力矩简化中心如图2 b)所示,规定其往列车方向倾覆即往内侧倾覆时力矩为正,反之力矩为负。

图3 广告牌分块及测点位置示意图
计算区域采用四面体进行网格划分,在列车尾部及广告牌附近区域进行网格加密,滑移计算区域和固定计算区域之间通过交界面传递数据。采用Fluent软件进行数值模拟计算,湍流模型选用k-ωSST模型,压力-速度关联算法采用Simplec方法。
为了减小由于网格尺寸引起的计算误差,应选取合理的网格尺寸。通过对比分析,最终选取了1种较为理想的网格尺寸:网格第一层高度为0.5 mm,边界层数为6层,车体和广告牌表面最大网格尺寸分别为80 mm和75 mm,网格单元为2 708万个。
3 仿真计算结果分析
为研究在不同列车运行速度下的广告牌受压变化规律,考虑到深圳地铁最高运行速度为120 km/h,香港地铁最高运行速度为135 km/h,本文选取的列车运行速度分别为80 km/h、100 km/h、120 km/h、140 km/h和160 km/h。以运行速度为140 km/h为例,分析列车通过时广告牌表面的压力分布和气动力特性。
3.1 广告牌表面压力分布
图4为广告牌表面纵向位置上x=1.5 m处不同高度测点的压力波动曲线。由图4可知:列车头部和尾部通过测点时会引起压力剧烈波动,产生头波和尾波;列车头部通过测点时产生的压力波动正波幅值、负波幅值和全波幅值都比尾部通过时大。因此,本文讨论的压力幅值均为头波幅值。同一纵向位置(x相同)处测点压力正波幅值、负波幅值和全波幅值从上往下逐渐增大。
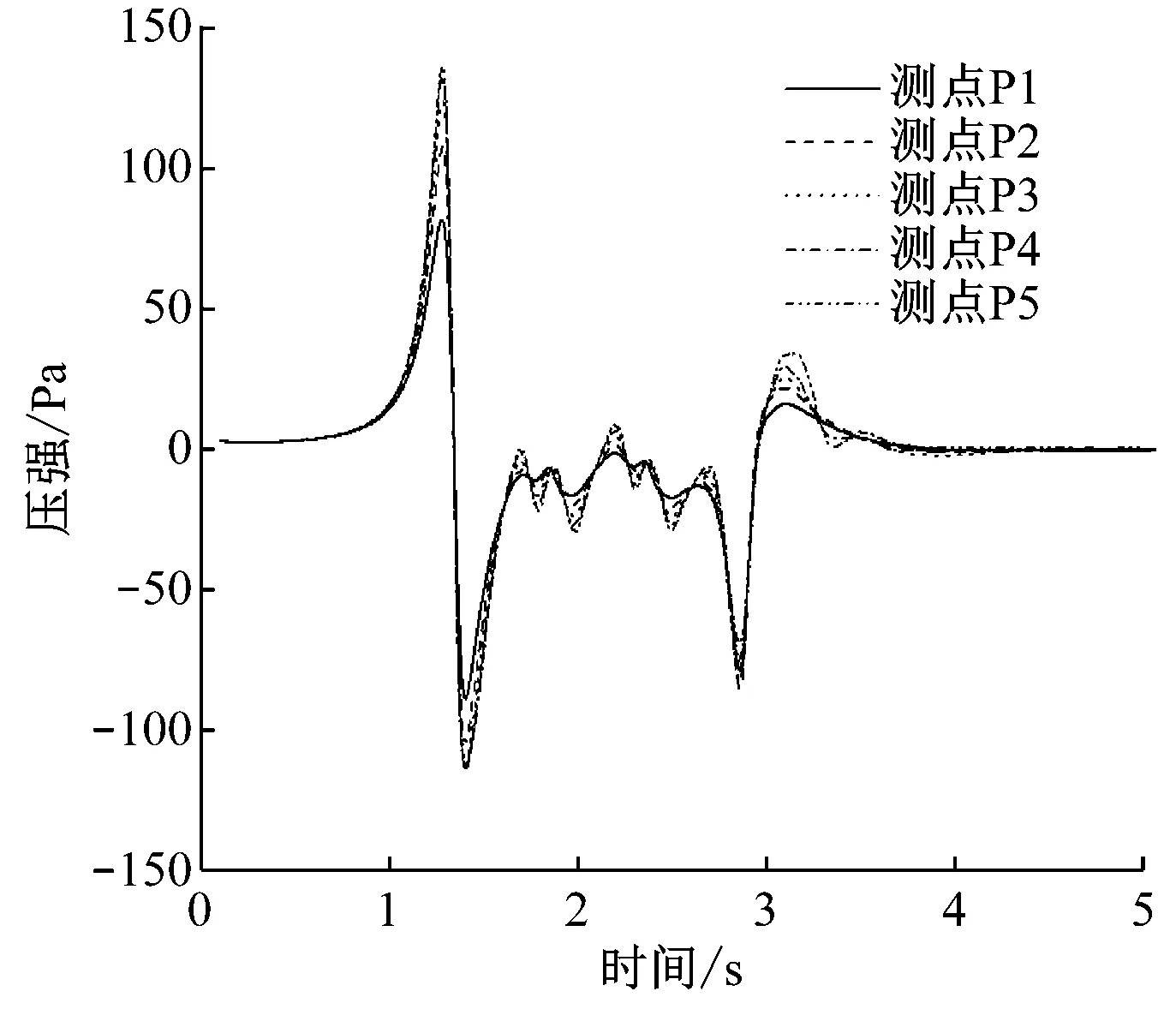
图4 广告牌表面x=1.5 m处测点压力波动曲线
图5和图6分别为列车头部通过广告牌中间位置时列车前端截面广告牌压力分布云图和广告牌附近的三维流线图。由图5~6可知:广告牌截面压力从上往下逐渐增大,广告牌外侧有负压区,顶部位置负压较大;广告牌上的头车鼻尖前部有一正压区,其后部有一负压区;广告牌顶部形成了一个涡柱,可能会引起广告牌振动;正压区和负压区的影响范围主要分布在x=6~7 m区域。
图7为不同高度上测点压力波幅值沿运行方向变化规律。由图7可知,中间位置(x=9.5~25.5 m)处为稳定区,压力基本相同;在同一高度处,压力最大值先增大后减小,然后稳定,后又继续减小,列车头部进入稳定区前压力达到最大值。邻近稳定区的前、后两个位置(x=5.5 m和29.5 m处)的测点压力峰值比其他位置大。当列车靠近广告牌,但还未驶入广告牌区域时,列车从空旷区域驶入相对受限环境。刚开始,列车前部被挤压的空气只有一部分进入受限区域;随着列车前行,空气将更多地进入受限区,广告牌上正压区逐渐增大,压力上升;当列车驶入广告牌区域时,广告牌上只有正压区,压力达到最大;当列车继续前行时,正压区后能形成负压区,被限制的空气可从负压区流走,压力降低,达到一个相对稳定的状态,形成稳定区;当列车头部位置驶出广告牌区域时,列车从相对受限环境驶入空旷区域,前方受挤压空气大部分从端部向四周扩散,列车继续往前行驶,广告牌上的正压区逐渐脱离广告牌,正压区减少,负压幅值增大。
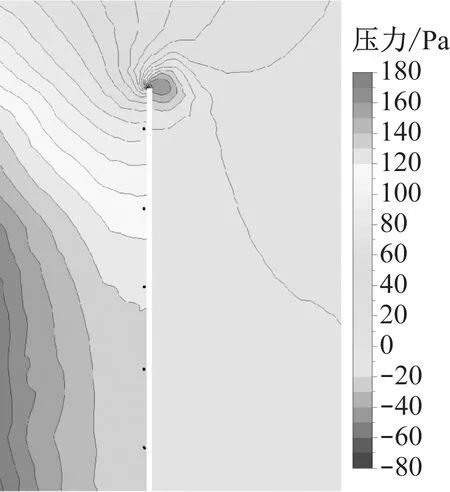
图5 广告牌截面压力分布云图

图6 广告牌附近三维流线图
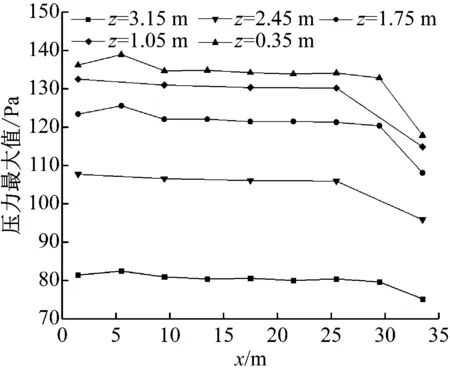
a)测点压力最大值
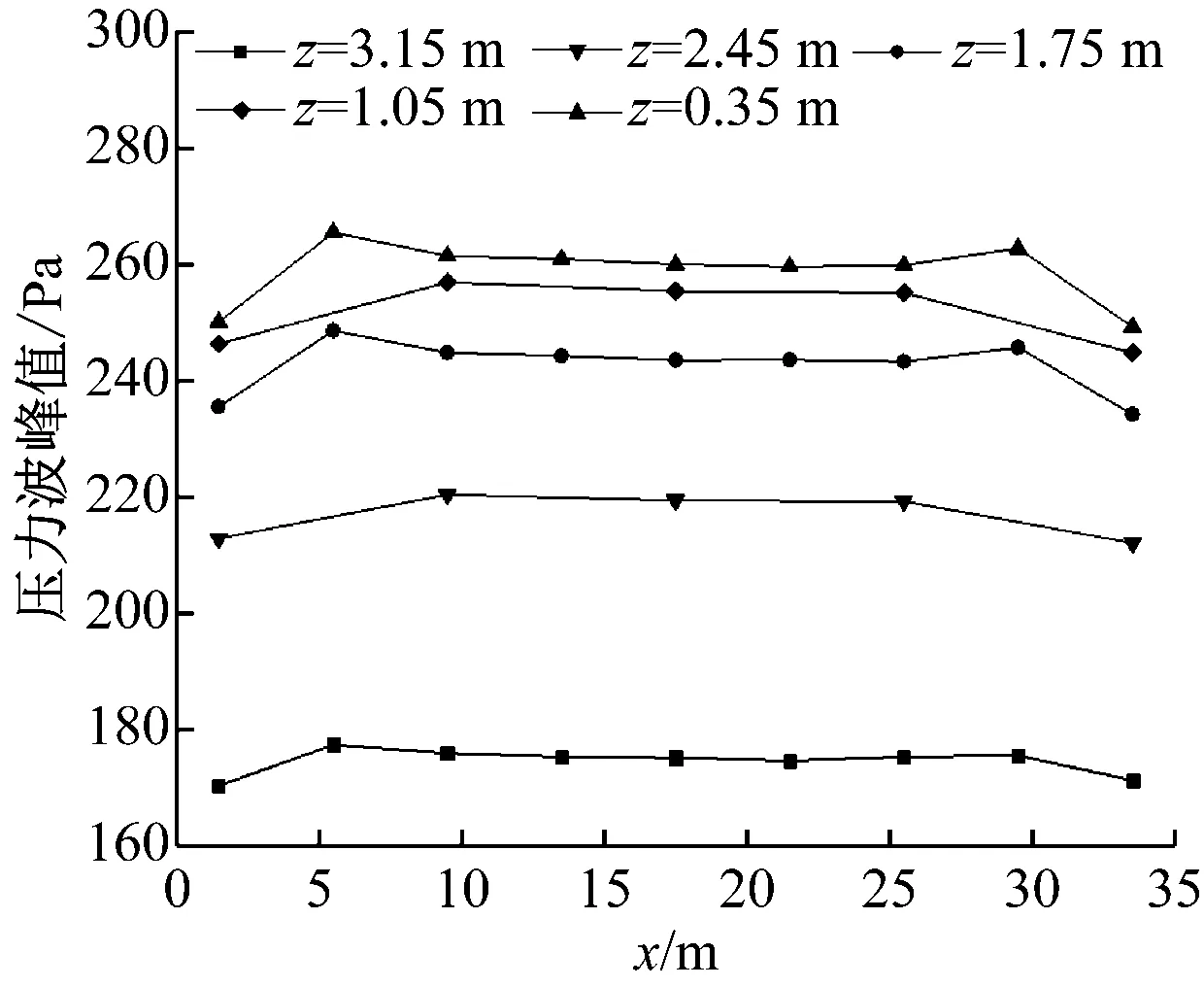
b)测点压力峰值
广告牌稳定区位置(x=9.5~25.5 m)与两端位置(x=1.5 m和x=33.5 m)相比,压力峰值有所增加。稳定区最大压力比两端至少大4.4%。最大压力峰值在x=5.5 m和x=29.5 m处,比两端至少大6.2%。可见广告牌稳定区受到的压力最大。根据压力峰值特征,新建了列车通过长度为6 m广告牌的计算模型,并在35 m长广告牌模型两端增加了压力测点以便比较。仿真计算结果见图8。
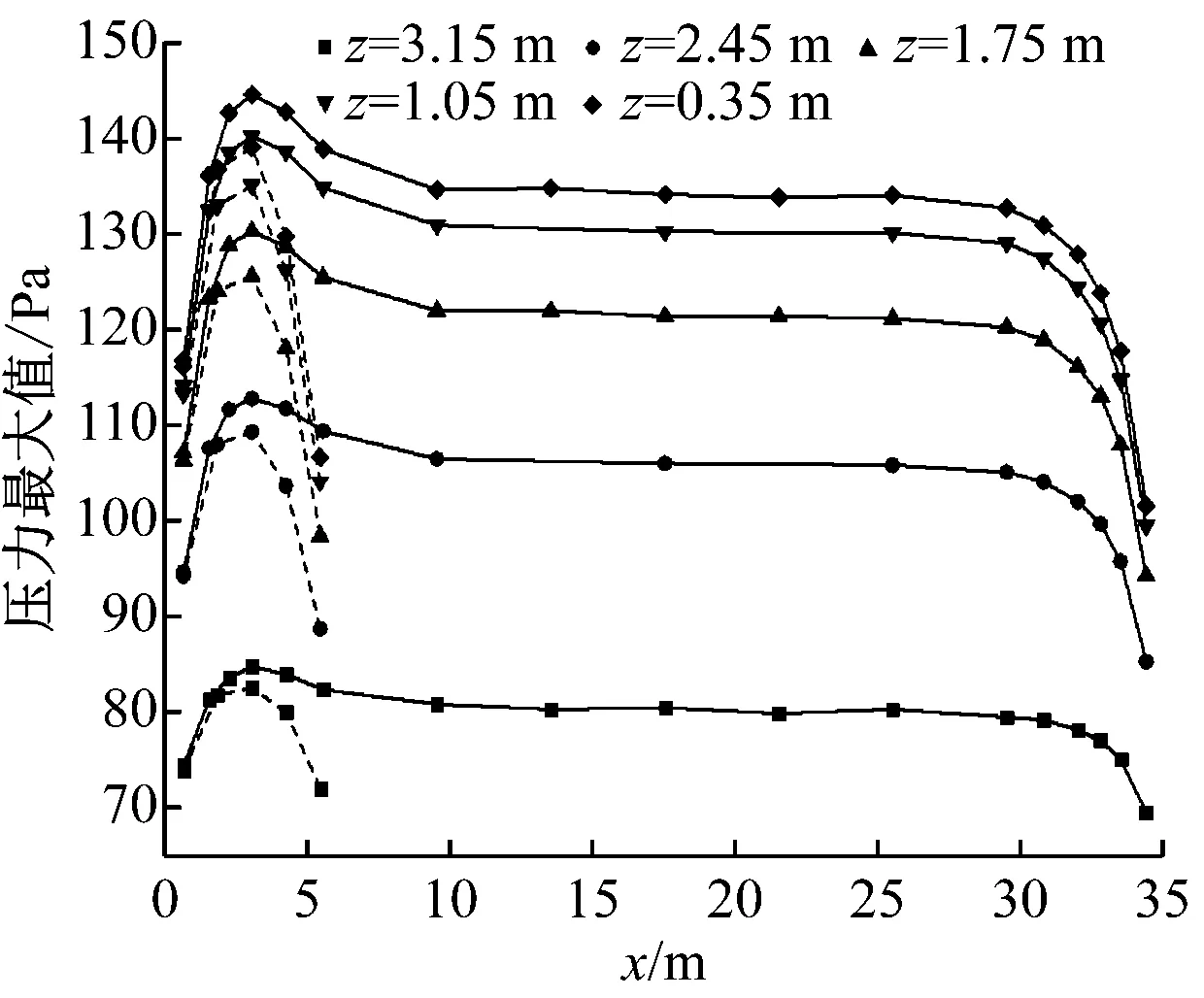
a)测点压力最大值
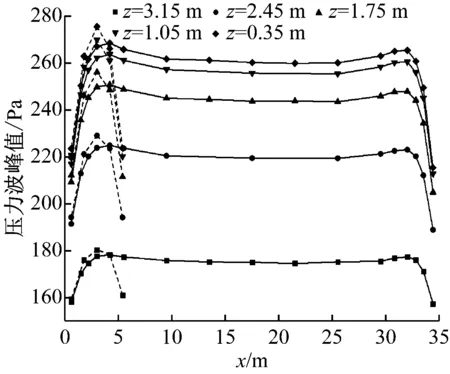
b)测点压力峰值
图8表明:只有广告牌达到一定长度才会产生稳定区;同一高度,6 m长广告牌的正波幅值最大值比35 m的小,负波幅值最大值与35 m的基本相同,峰值比35 m的大。35 m长广告牌正波幅值和负波幅值最大值分别在广告牌两端;当广告牌长度为6 m时,正波幅值和负波幅值最大值集中到了一个位置,因此,6 m长广告牌的压力峰值变大。
图9为不同x处测点压力峰值沿z变化曲线。对x相同而z不同的测点压力峰值采用幂函数形式进行拟合,有:
P=-azb+c
(2)
式中:
P——测点压力峰值;
a、b、c——相关参数,与列车外形、广告牌大小及位置等有关;当z=0时,c即为广告牌与地面接触位置的压力。
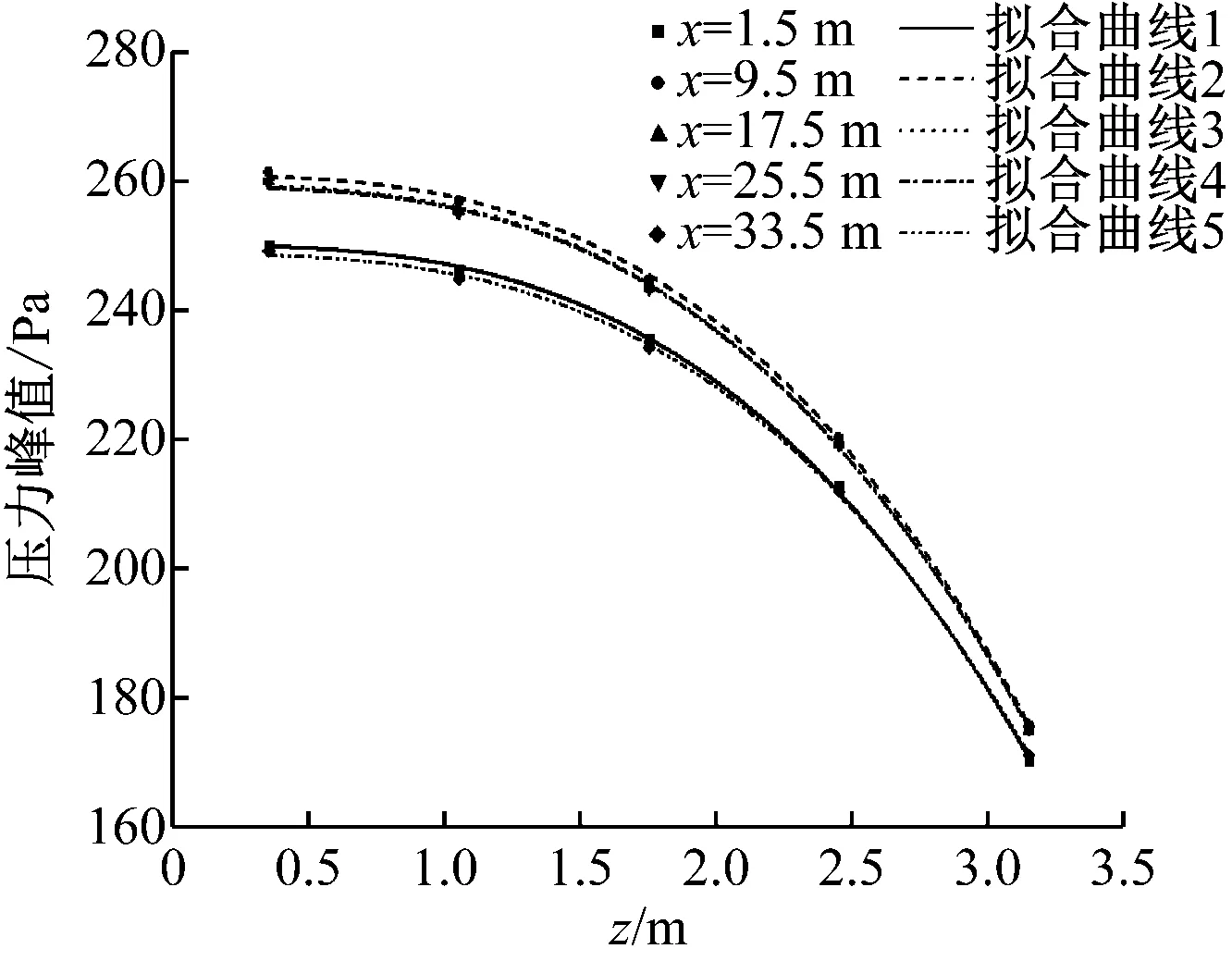
a)压力峰值
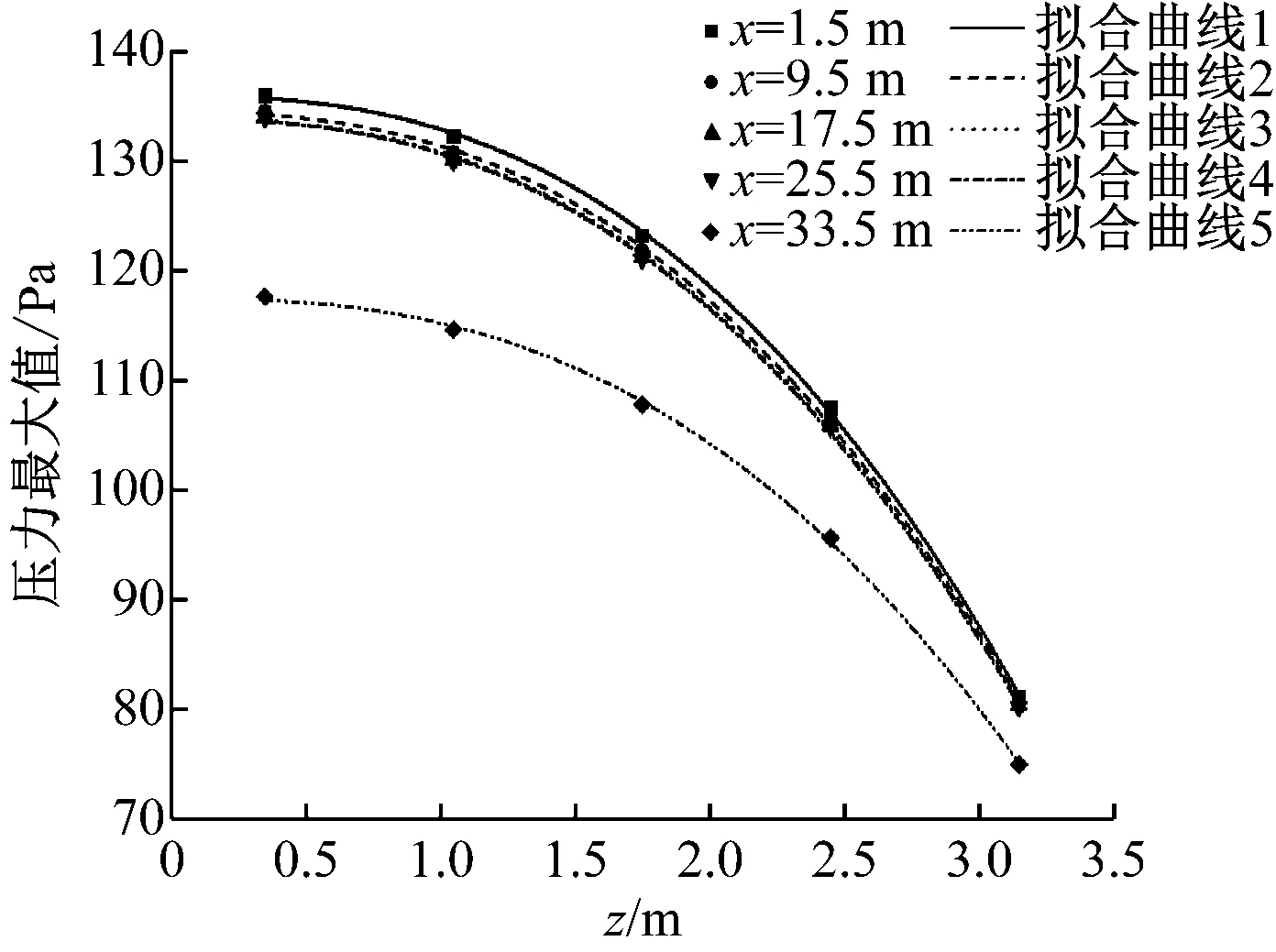
b)压力最大值
根据拟合结果,当列车匀速通过不同纵向位置时,压力峰值随z变化趋势基本相同,即可求得b值。将b值平均值作为幂次数,进行再次拟合。拟合结果显示,拟合曲线的修正相关系数都在0.999以上,非常接近1,说明压力峰值与z之间的确为幂函数关系。类似地,对压力正波幅值和负波幅值分别拟合,得到b分别为2.517 5和3.673 7,其修正相关系数也都非常接近1,说明幂函数关系适用。
3.2 广告牌气动力特性
图10为广告牌不同高度监测块受到的侧力和倾覆力矩变化曲线。从图10可知:侧力和倾覆力矩的头波峰值均比尾波峰值大(在后文讨论中的气动力峰峰值均为头波峰峰值)。由图10还可见:随着高度的增加,侧力的正波幅值、负波幅值和全波幅值都逐渐减小;对于同一监测小块,当列车头车通过时,广告牌所受侧力先向外侧,再向内侧。而且往外侧方向的倾覆力矩较往内侧的大。
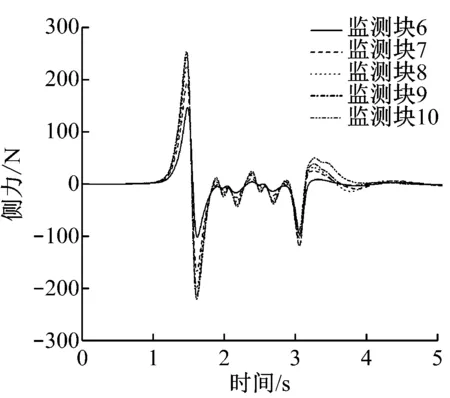
a)x=9.5 m处侧力波动曲线
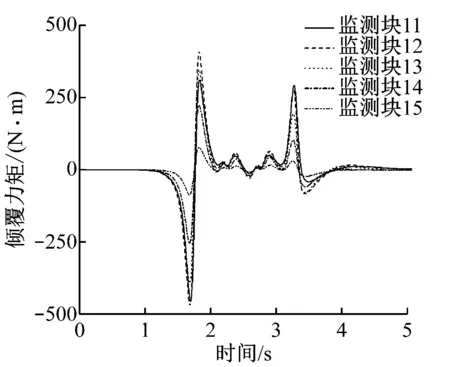
b)x=17.5 m处倾覆力矩波动曲线
由图11可知,广告牌两端所受侧力及倾覆力矩较小,中间位置受力较均衡,且前端比后端稍大。对x相同、z不同的5块区域侧力和倾覆力矩进行求和,即得广告牌x处受到的总侧力和倾覆力矩(如图12)。侧力头波正波幅值大于负波幅值,倾覆力矩头波负波幅值大于正波幅值。总侧力和总倾覆力矩的变化规律基本一致:广告牌前端受到的气动力最大,末端最小,中间基本相同。
由总气动力计算结果可知:稳定区侧力峰值比x=1.5 m处大9.3%,倾覆力矩峰值比x=1.5 m处大10.1%。稳定区位置与两端位置相比,广告牌所受气动力有所增加。
侧力正波幅值、负波幅值及全波幅值同z的关系采用幂函数形式拟合,得到b分别为2.399 2、3.338 4及2.820 4,其最小修正相关系数分别为0.999 4、0.997 4和0.998 7,都非常接近1,说明侧力正波幅值、负波幅值和峰峰值与高度之间的确为幂函数关系。
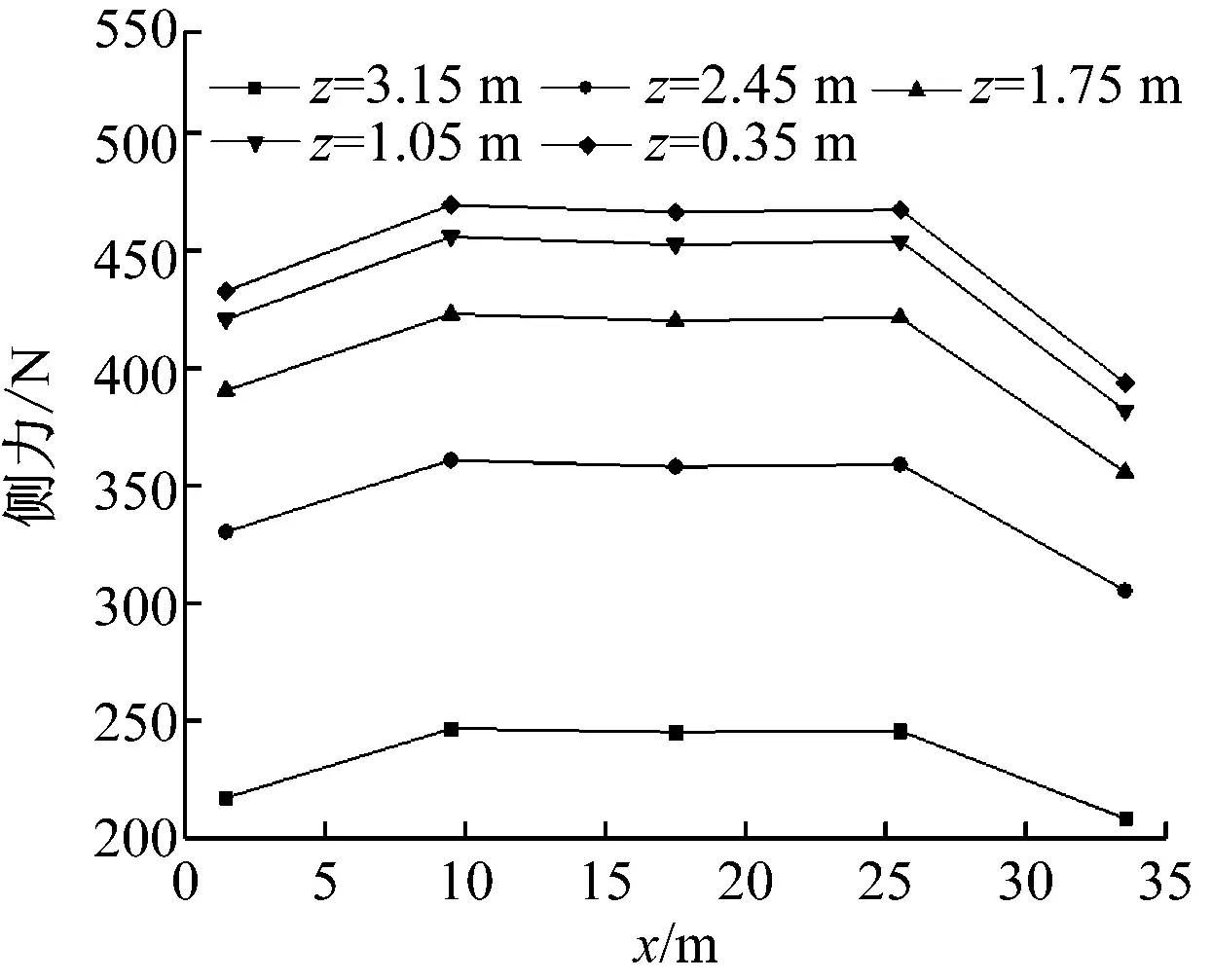
a)侧力
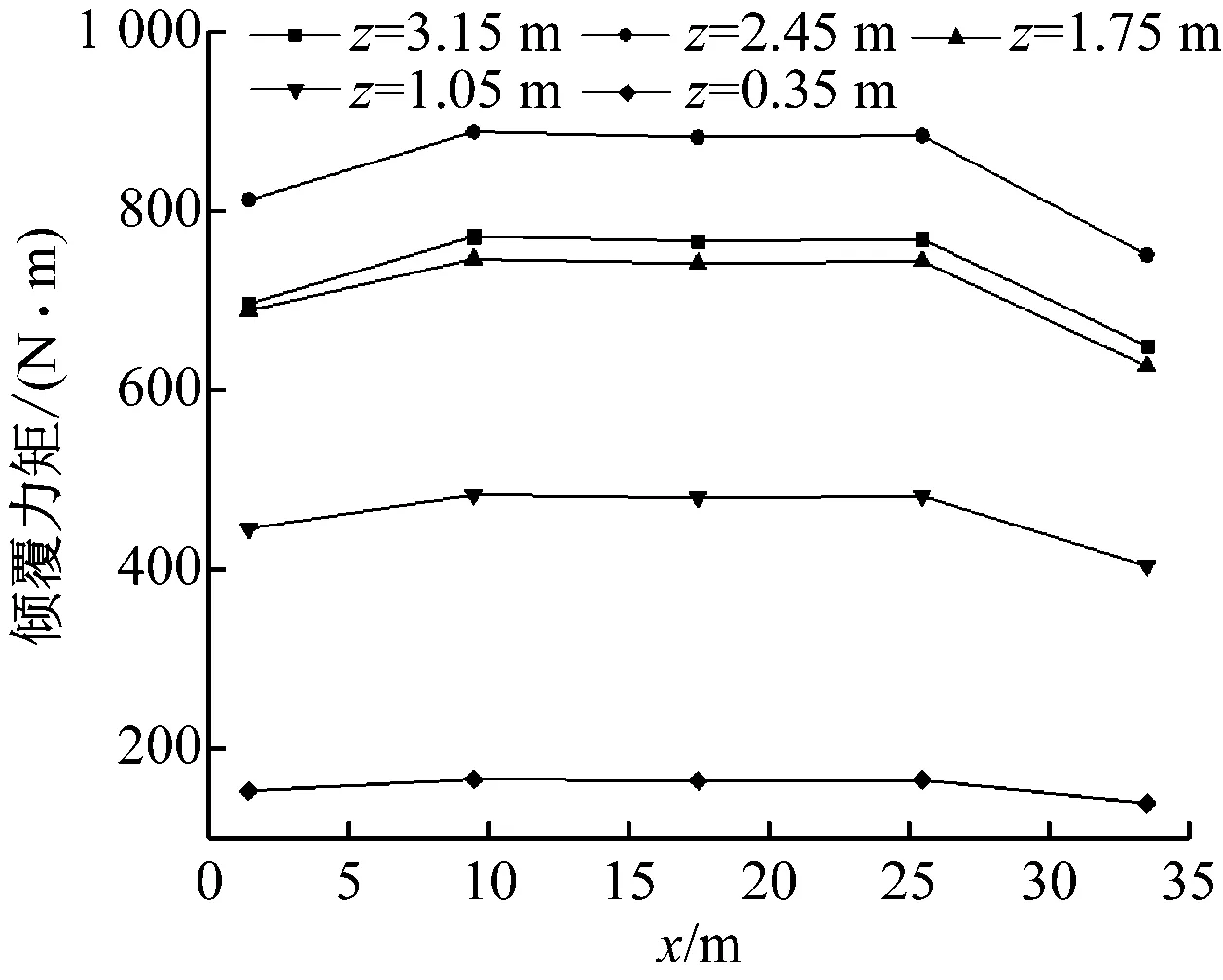
b)倾覆力矩
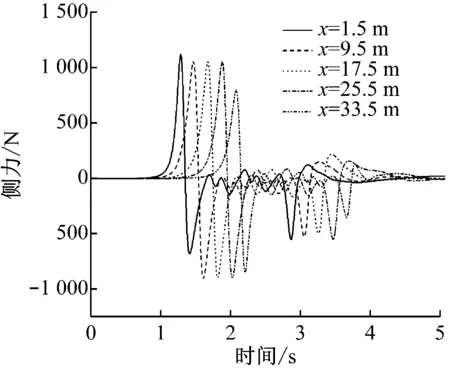
a) 侧力
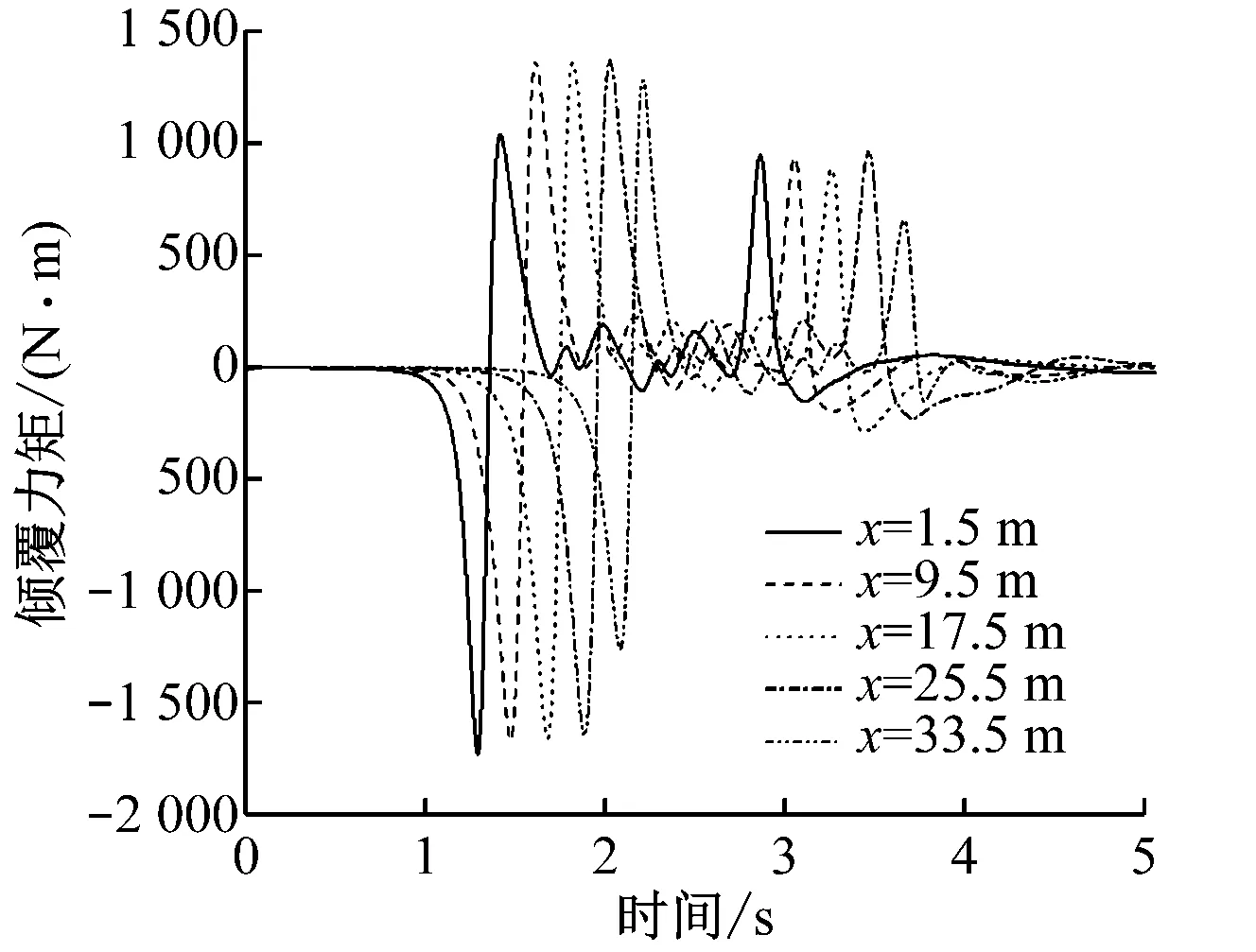
b) 倾覆力矩
3.3 列车运行速度对广告牌受力的影响
不同列车运行速度对广告牌表面压力影响为:
(3)
式中:
Cp——压力系数;
P——广告牌表面压力;
ρ——空气密度;
vt——列车运行速度。
图13为不同vt下列车通过广告牌时测点P8的压力变化曲线和Cp曲线。从图13中可以看出,由于列车vt不同,列车到达测点时刻不同,引起的压力波动幅度也不同;而Cp曲线头波正波幅值、负波幅值和全波幅值基本相同,最大差异分别为1%、0.5%和0.3%。因此,同一位置不同列车速度下的Cp可认为相同。那么,对于广告牌表面相同位置处的P与vt关系可写为:
(4)
式中:
P1,P2——分别为vt1及vt2对应的压力;
C——常数。
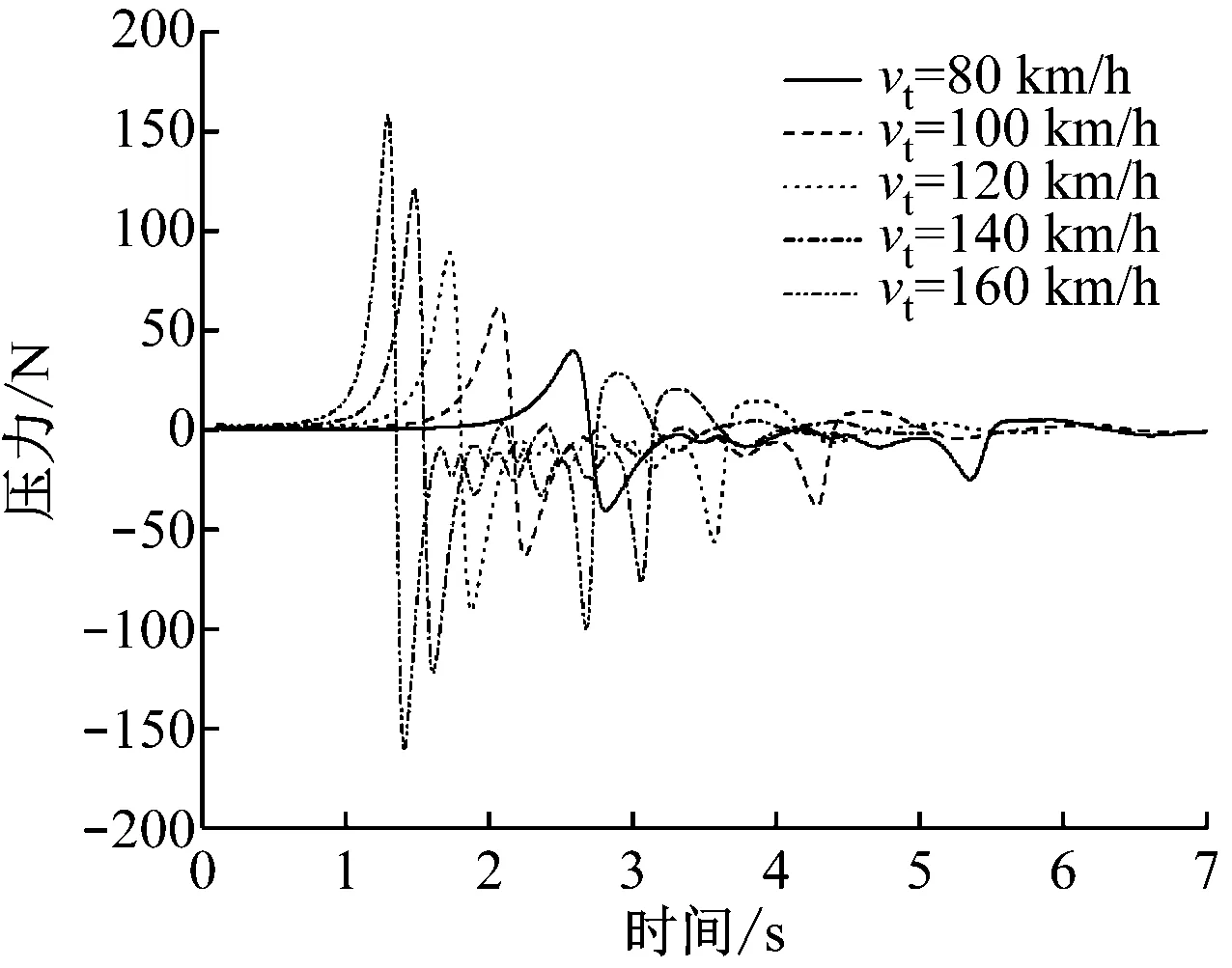
a) 压力曲线
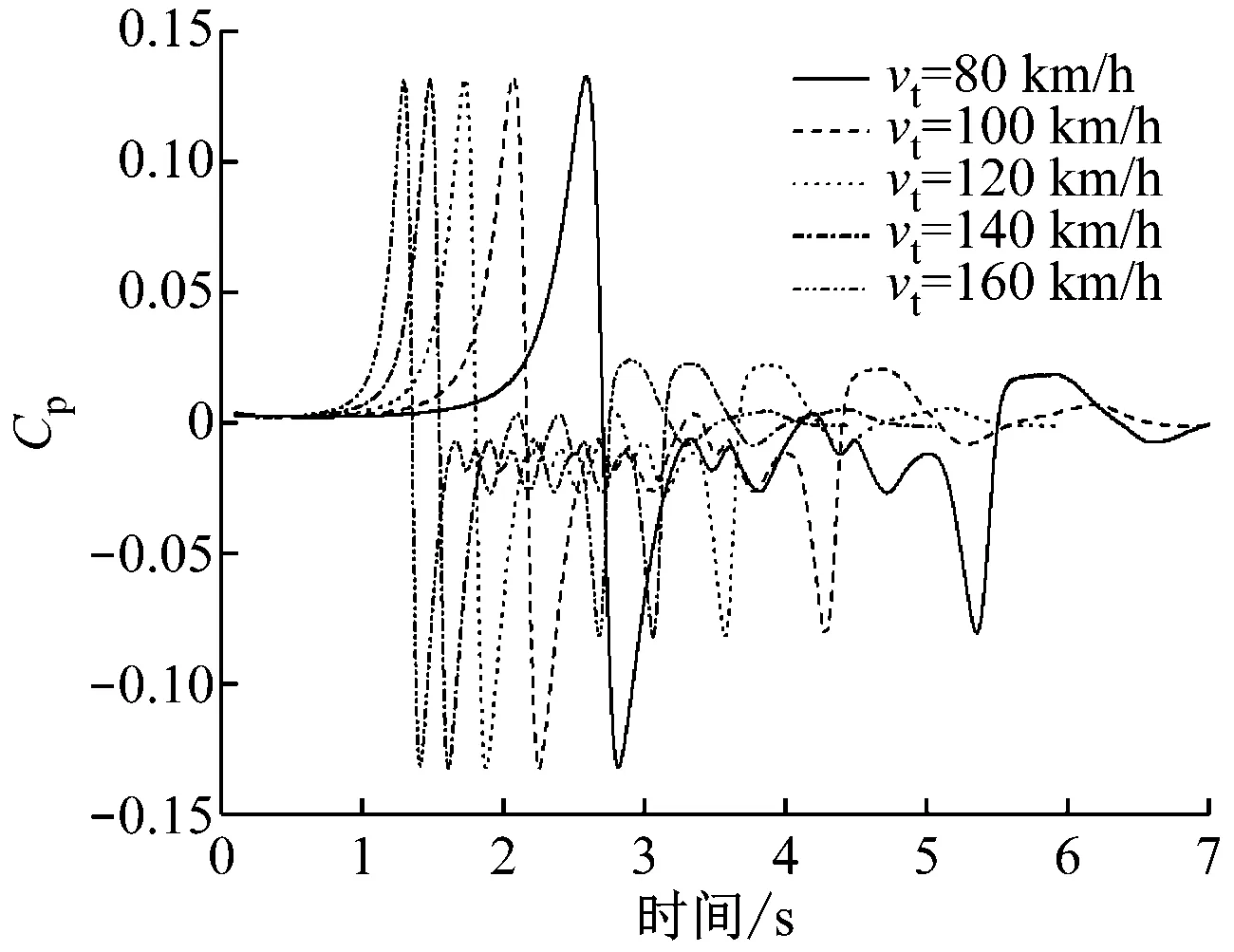
b) Cp曲线
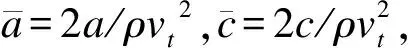
(5)
对不同vt下测点压力峰值与z关系进行拟合,可得到不同vt下的b。b平均值显示,不同vt对应的b相差不大。取不同vt下的b平均值2.912 3作为b的统一值。采用此幂次数值,对不同vt下不同x处的P峰值与z之间关系进行拟合,得到拟合系数。
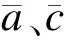
因此,x相同且z不同处P为:
(6)
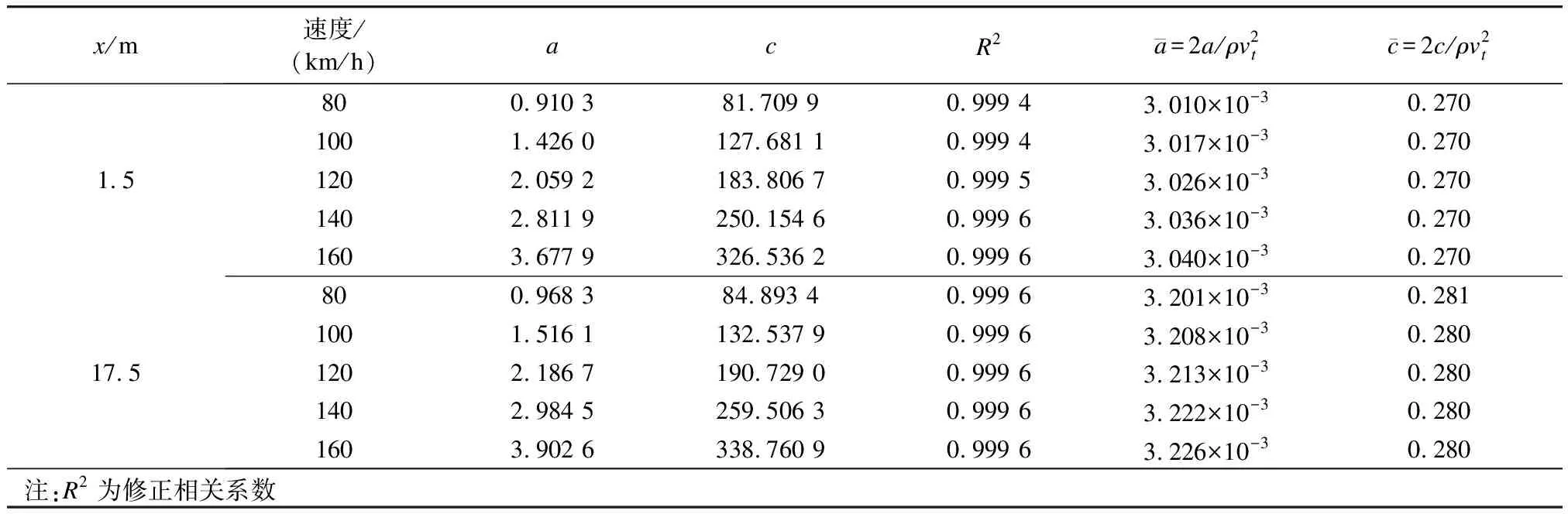
表1 不同vt下拟合系数部分
类似地,对压力和侧力的正波幅值、负波幅值,以及侧力峰值进行同样的处理,也可得到如式(6)的形式。
图14为不同vt下列车通过广告牌x=9.5 m处总倾覆力矩变化曲线。从图14中可以看出,不同vt,对应的倾覆力矩波动幅度不同。而倾覆力矩系数曲线波动基本相同,倾覆力矩系数峰值最大差异为0.29%。
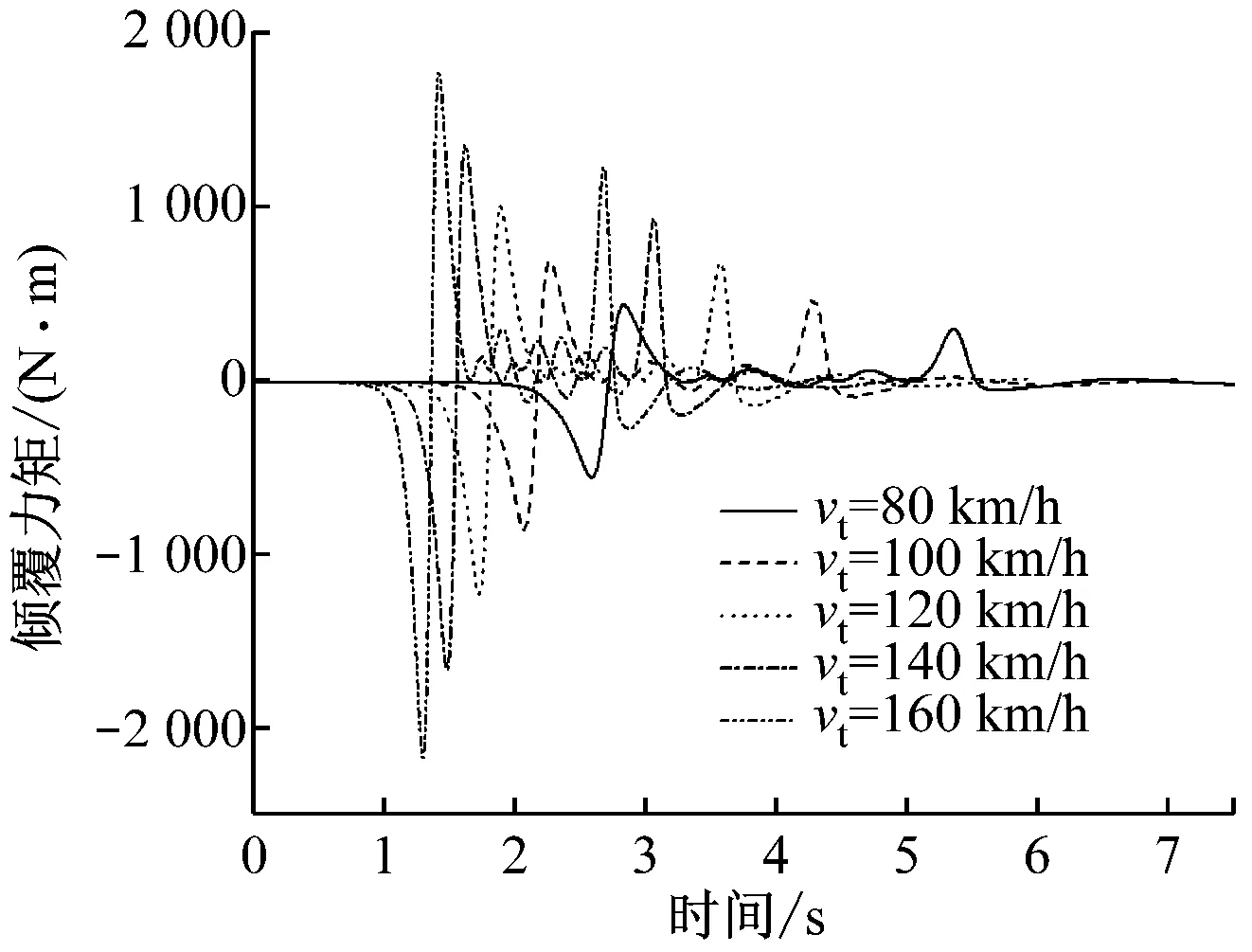
a)倾覆力矩变化曲线
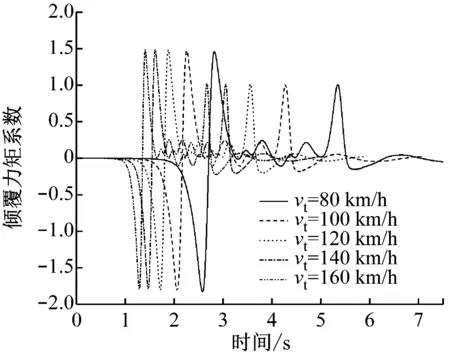
b)倾覆力矩系数变化曲线
对于固定于某一位置的广告牌,其自身高度、距离轨道距离等已确定,若已知某一速度下的压力、侧力和倾覆力矩,即可以根据压力系数、侧力系数、倾覆力矩系数不变的特点,采用式(4)确定不同vt时广告牌受到的压力和气动力。
4 结论与建议
(1)列车头部通过广告牌时的测点压力峰值、监测块侧力峰值及倾覆力矩峰值比列车尾部通过时大。
(2)同一纵向位置,测点压力和监测块侧力的头波正波幅值、负波幅值和全波幅值均随高度增加而减小,压力和侧力都与高度呈幂函数关系,且不同vt下的幂次数相同。同一高度上的测点压力最大值沿运行方向先增大后减小,然后稳定,后又继续减小,压力最小值幅值变化与之相反。
(3)在x=5.5~29.5 m之间的压力峰值最大值比两端位置(x=1.5 m和33.5 m处)最大值大6.2%,稳定区侧力和倾覆力矩峰值比两端位置最大值分别大9.3%和10.1%;广告牌达到一定长度才会产生稳定区,稳定区内同一高度上测点压力、侧力和倾覆力矩波动情况一致。广告牌长度为6 m时,同一高度的正波幅值最大值比35 m长的广告牌小,负波幅值最大值与35 m长的广告牌基本相同,峰值最大值比35 m长的广告牌大。
(4)不同vt下,Cp、侧力系数及倾覆力矩系数曲线特征幅值几乎一致。若已知在vt下的广告牌压力和气动力分布,则可根据系数不变特性得到目标速度下广告牌的压力和气动力参数。
为了减缓气动力对广告牌的影响,建议广告牌安装位置在允许范围内尽量远离轨道,并保证其距离地面有一定空间;广告牌宜采用连续间隔的布置,且每个广告牌长度应控制在6 m范围内。

