配置直线不等长预应力筋简支梁自振频率研究

郭凯强， 贾艳敏， 于广龙， 王佳伟, 张冠华

(1.东北林业大学 土木工程学院，哈尔滨 150040；2.辽宁省交通规划设计院有限责任公司公路养护技术研究中心，沈阳 110101)

预应力混凝土简支梁桥是我国桥梁工程中应用最广泛的结构形式之一，因此，对其自振频率的准确计算显得尤为重要。近年来国内外对简支梁桥的振动特性进行了大量研究[1-4]，Saiidi等[5]通过室内和现场试验，得出了预应力与混凝土梁自振频率的关系，预应力越大自振频率越大。Miyamoto等[6]采用初等梁理论，推导了预应力钢混组合梁的自振频率计算公式，并分析了体外筋及偏心距对自振频率的影响。熊学玉等[7]对Miyamoto提出的公式进行了修正和扩充，分析了体外预应力混凝土梁的振动特性，分别推导了体外预应力筋不同布置方式下的自振频率计算公式，并对其影响因素进行了探讨。肖静霆等[8]认为预应力钢筋的拉力与梁所受的压力均属于结构的内力，预应力的大小不影响其动力特性。张家玮等[9]研究了考虑初始荷载影响下梁动力特性的有限元分析，通过建立有限元方程讨论了各因素对梁自振频率的影响。黄萍[10]通过室内试验研究分析了预应力混凝土简支梁频率的变化及动刚度随荷载增加而退化的规律。张书冰等[11]通过4根简支钢-混组合梁的模态试验证明了修正刚度折减法在组合梁自振频率计算中的使用范围更广。谭国金等[12]研究了无黏结偏心直线预应力筋简支梁的自振频率计算，得出了自振频率与偏心距和预加力之间的关系。杨殊珍等[13]研究了环境温度和边界条件对混凝土梁式桥自振频率的影响，得出了在不同结构形式下二者对梁式桥自振频率的影响权重不同。

综上所述，现有对桥梁固有频率的研究有三类方法，即理论推导、有限元模拟和室内试验，缺乏实桥验证，并且对偏心直线不等长预应力筋简支梁自振频率的研究相对较少。本文基于既有理论研究成果，提出了不等长预应力筋简支梁自振频率的计算公式，并与现场试验值以及有限元分析值进行对比分析，验证了公式的合理性和准确性，实现了对实际工程中此类梁自振频率的求解。

1 自振频率理论分析

1.1 基本假定

本文在推导不等长预应力筋简支梁自振频率计算公式时做出如下假定：①服从Euler-Bernolli梁理论，即忽略梁的剪切变形；②不考虑预应力筋与混凝土粘结滑移的影响，二者变形协调一致；③不考虑预应力引起的反拱，即初始状态下梁轴线保持平直；④不考虑阻尼的影响，即梁的振动为自由振动。

1.2 理论计算公式

图1为直线配筋有粘结预应力混凝土简支梁，其中预应力筋有效长度均不相同。在钢筋的两端点作用一对预加力，偏心距为e，由于是偏心受压，那么除了在梁纵向产生一个合力为p0的轴向压力外，还会产生一个附加力偶，其合力偶值为：M0=p0e。

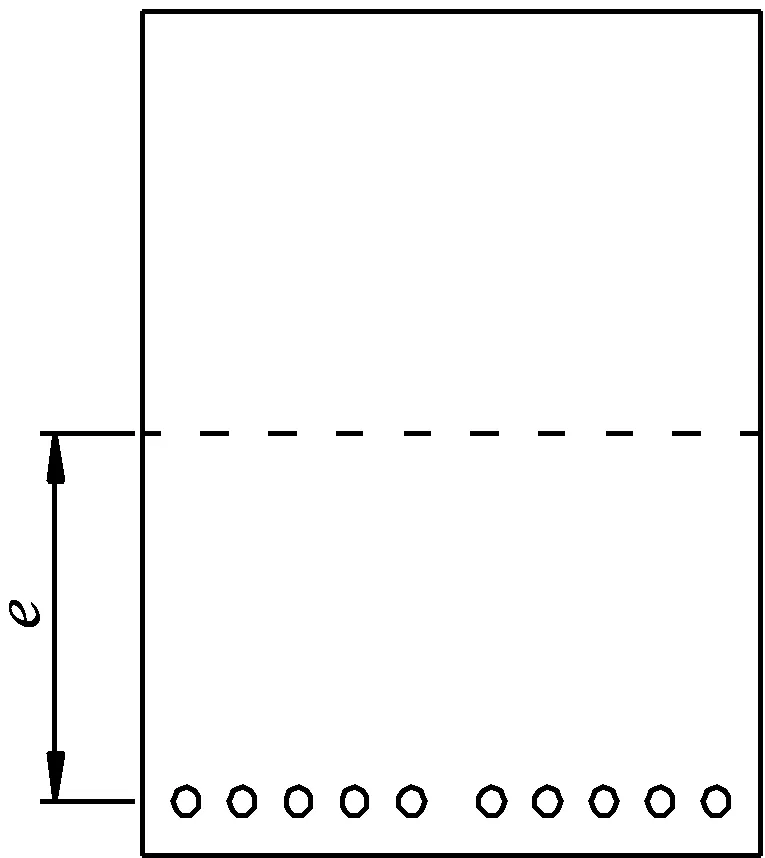
1234554321

预应力筋有效长度表

图1 直线型布筋简支梁模型图

Fig.1 Model of unequal prestressed reinforcement simple supported beam

由于梁在振动过程中，梁两端的预应力是不断变化的，因此，可设：

(1)

Δp是预应力的改变量，随振动位移的变化而变化。设简支梁有λ种不同长度的预应力筋，预应力筋总截面积为A，任意长度的预应力筋与梁的力学模型，如图2所示。

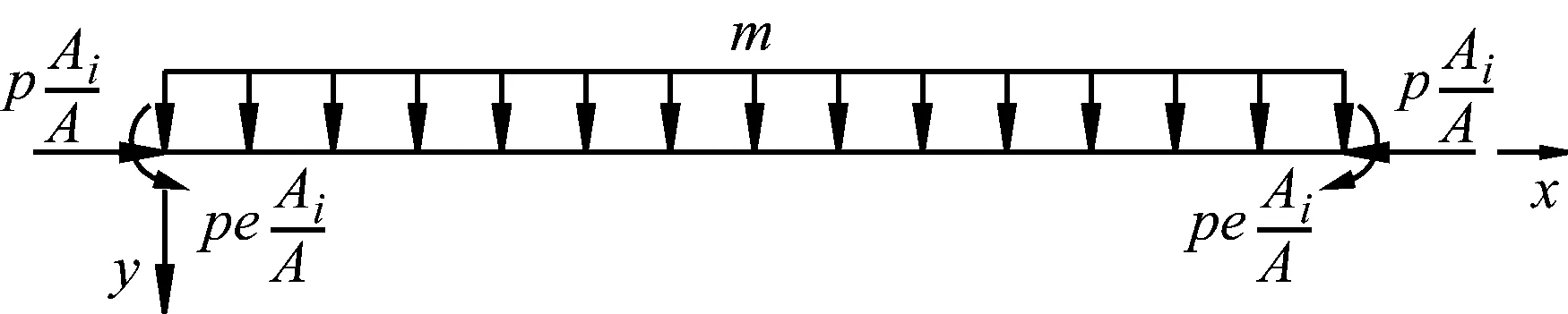
图2 任意长度预应力筋与梁的受力图

Fig.2 Force diagram of prestressed reinforcement of any length and beam

梁在预应力作用下的弯曲振动微分方程可由梁的自由振动方程可得出

(2)

式中：E为梁的弹性模量；I为梁截面惯性矩；y为振动位移；m为梁单位长度质量。

将式(1)代入式(2)可得

(3)

考虑y远小于e，所以Δpy可忽略不计，又因为p0是初始时所施加的预应力，为一恒定的常数，所以有

(4)

整理式(3)得

(5)

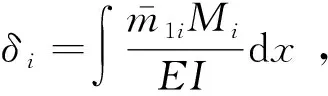
(6)

SMi为图3中Mi图的面积，而在钢筋端点作用单位力引起的该端点的水平位移可由下式计算

(7)

图3 梁的内力

Fig.3 Internal force diagram of beam

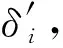
(8)

由式(8)可得由F引起所有钢筋锚固力的变化为

(9)

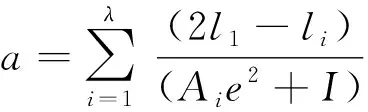
而在力F作用下梁跨中的位移为

(10)

将式(9)代入式(10)可得

(11)

由位移互等定理可知，Δp在梁跨中产生的向上位移yΔp为

(12)

(13)

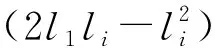
(14)

这样，根据关系式y=yF-yΔp与式(11)、(14)，可得

(15)

则

(16)

其中

(17)

即

(18)

将式(18)代入式(5)可得

(19)

式(19)即为不等长预应力筋简支梁的自由振动方程，对于式(19)，根据振动的基本理论，可采用分离变量法求解。可设

y=Y(x)·(cosωnt+jsinωnt)

(20)

式中：ωn为其固有圆频率；n为自然数；j为虚数单位。

将式(20)代入式(19)，并整理可得

(21)

对于所分析的简支梁，根据文献[7]可设Y(x)的表达式为

(22)

式中：ψ为常数。

将式(22)代入式(21)可得

(23)

解式(22)可得

(24)

式(24)即为所求的梁的自振圆频率，其中

(25)

由梁的自振圆频率可求得其自振频率为

(26)

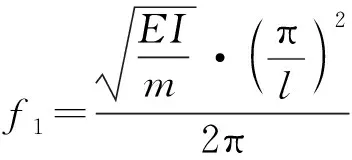
2 方法对比分析

2.1 试验梁模态试验

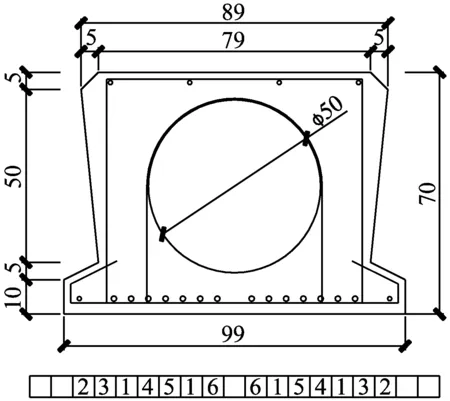
试验梁所属桥梁位于沈四(沈阳至四平)高速铁岭地段。上部构造为16 m先张法PC空心板梁，采用C40混凝土，预应力筋为Φj15.24(7Φ5)钢绞线，标准强度1 860 MPa，张拉控制应力为1 395 MPa。如图4为试验梁横截面图和钢筋布置图，图5为现场试验照片。

预应力筋有效长度表

编号123456长度1 5961 4601 1901 060930690

(a) 横截面布置图

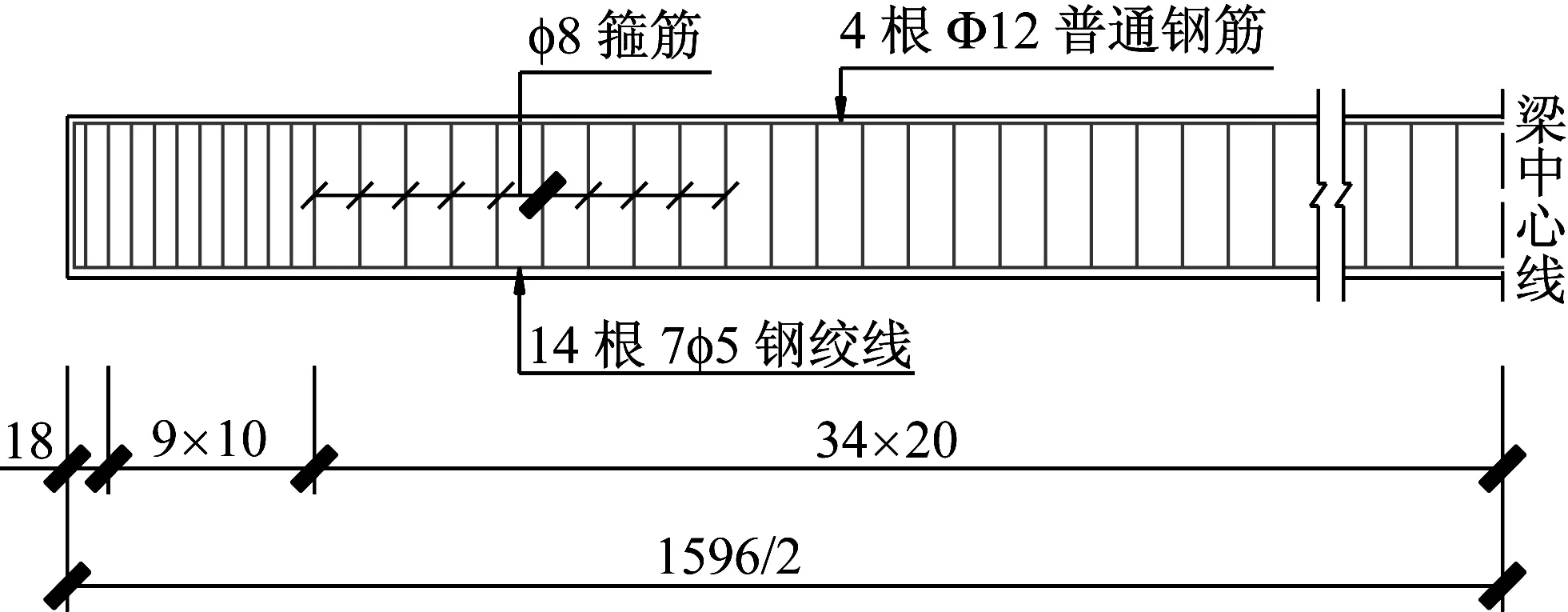
(b) 钢筋布置图图4 试验梁的横截面及预应力束布置示意(cm)Fig.4 Test beam cross section and prestressed tendon layout(cm)

图5 现场试验照片Fig.5 Field experiment photo

本次动测试验采用江苏东华测试技术有限公司研发的东华桥梁模态测试系统，主要试验仪器包括传感器、路由器、笔记本电脑以及DHDAS信号测试分析软件等，测点布置分别在支点、1/4跨、跨中及3/4跨位置处，采用自然脉动激励的方法对该试验梁进行激振，采样频率为100 Hz，分析频率为39.06 Hz，采用连续采样的采样方式，试验过程中采用GPS同步卫星测试模式，增强各传感器之间的同步性，图6为试验梁测点布置图。

图6 试验梁测点布置图Fig.6 Test beam measuring point layout

2.2 有限元模型的建立

采用有限元分析软件ANSYS建立预应力混凝土简支梁有限元模型。根据试验梁的特点，混凝土用实体单元Solid-65模拟，预应力筋与普通钢筋都以杆单元 Link-8来模拟[12]。按照原设计资料，分别建立预应力筋与普通钢筋模型，见图7。建模过程中采用约束方程法模拟混凝土与钢筋之间的作用，即钢筋单元的一个节点与混凝土单元的多个节点建立约束方程，通过多组约束方程，将钢筋与混凝土的单元连接成一个整体；预应力施加采取常用的降温法，并依照规范求解预应力损失。图8为有限元分析得到的前两阶竖向振型。

(a) 钢筋单元图

(b) 混凝土单元图图7 预应力混凝土空心板梁有限元模型Fig.7 Finite element model of prestressed concrete hollow slab beam

2.3 数据对比分析

应用式(26)对试验梁进行一阶和二阶频率计算，并对试验梁有限元模型进行模态分析。前两阶频率理论计算结果、现场试验结果和有限元计算结果见表1。

由表1可以看出，试验梁一阶和二阶自振频率的理论计算结果、有限元分析计算结果以及实测结果均非常接近，误差基本在5%以内，说明本文推导的理论计算公式和建立的有限元模型在计算前两阶频率上是较为准确的。

表1频率试验值、理论值和有限元值

Tab.1Frequenciesresultofmodelexperiment,theoryandfiniteelement

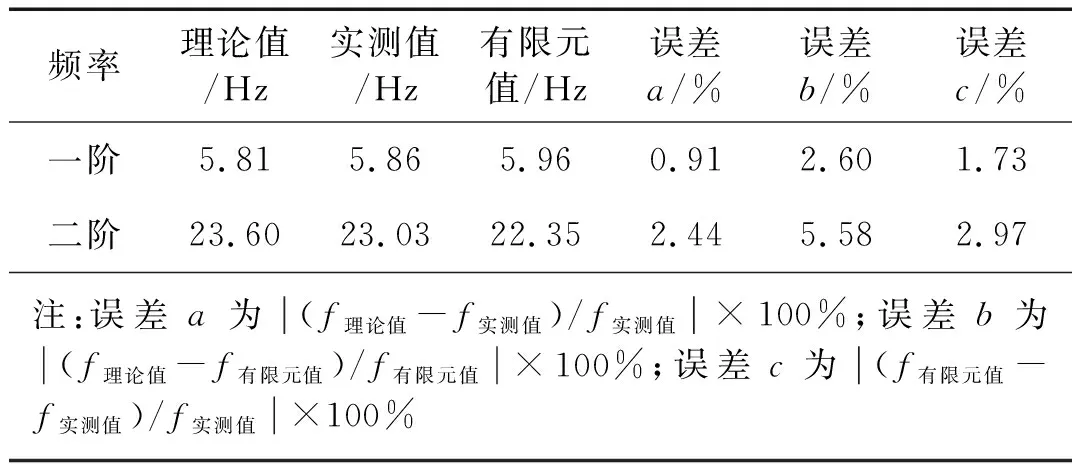
频率理论值/Hz实测值/Hz有限元值/Hz误差a/%误差b/%误差c/%一阶5.81 5.86 5.96 0.91 2.60 1.73 二阶23.60 23.03 22.35 2.44 5.58 2.97 注:误差a为(f理论值-f实测值)/f实测值×100%;误差b为(f理论值-f有限元值)/f有限元值×100%;误差c为(f有限元值-f实测值)/f实测值×100%

(a) 一阶竖向振型

(b) 二阶竖向振型图8 试验梁前两阶竖向振型图Fig.8 The first two vertical modes vibration modes of the test beam

3 自振频率影响因素分析

为了探讨预应力值和偏心距对不等长预应力筋简支梁自振频率的影响，采用本文计算公式和有限元法分别计算了同一偏心距情况下多组预应力值对应的简支梁第一阶自振频率，以及同一预应力值情况下多组偏心距对应的简支梁第一阶频率。

3.1 预应力的影响

偏心距取0.325 m，施加不同预应力的简支梁第一阶频率有限元计算和理论计算结果见表2。

由表2可知，偏心直线不等长预应力筋简支梁一阶频率随着钢筋预应力的增大而略有降低，而有限元计算结果变化很小。总体而言，钢筋预应力的大小对简支梁的一阶频率影响很小。故实际桥梁随着运营时间的增长，预应力损失情况对桥梁一阶频率影响很小。

3.2 偏心距的影响

钢筋预应力取1 100 MPa，不同偏心距情况下试验梁一阶频率的理论计算和有限元计算结果见表3。

表2预应力对简支梁第一阶频率的影响

Tab.2Theinfluenceofprestressvalueonnaturalfrequencyofsimplysupportedbeam

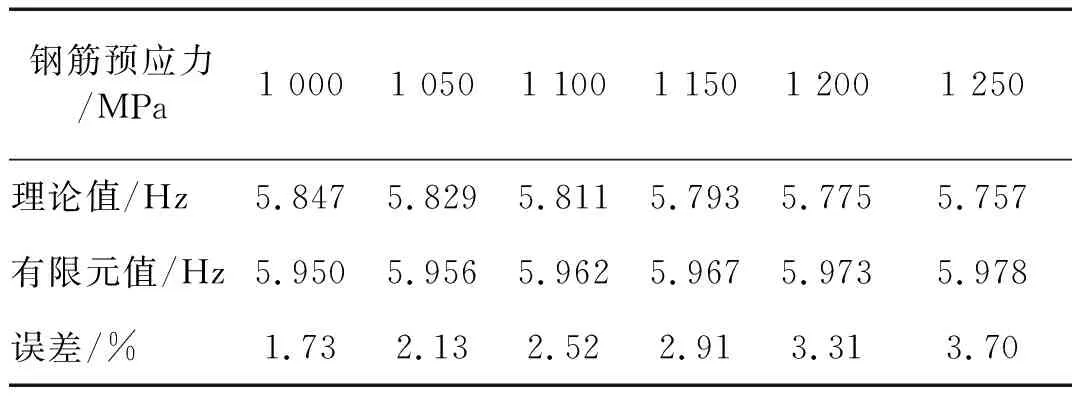
钢筋预应力/MPa1 0001 0501 1001 1501 2001 250理论值/Hz5.847 5.829 5.811 5.793 5.775 5.757 有限元值/Hz5.950 5.956 5.962 5.967 5.973 5.978 误差/%1.73 2.13 2.52 2.91 3.31 3.70

表3偏心距对简支梁第一阶频率的影响

Tab.3Theinfluenceofeccentricityonnaturalfrequencyofsimplysupportedbeam

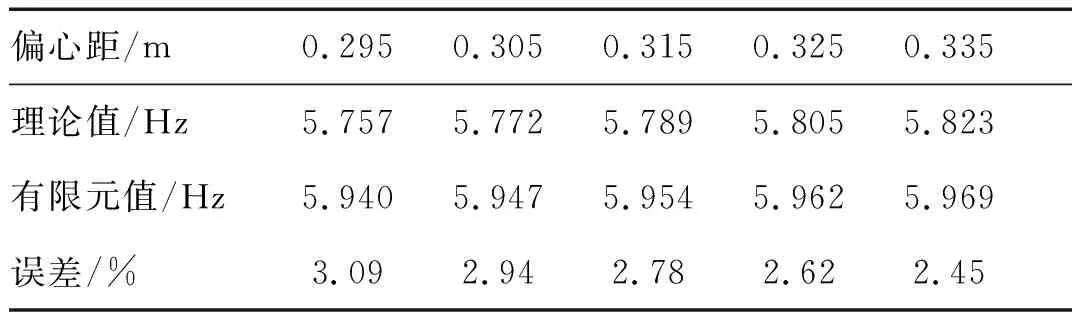
偏心距/m0.2950.3050.3150.3250.335理论值/Hz5.757 5.772 5.789 5.805 5.823 有限元值/Hz5.940 5.947 5.954 5.962 5.969 误差/%3.09 2.94 2.78 2.62 2.45

表3中只列出了偏心距在0.295～0.335 m之间的一阶自振频率计算结果，同理可计算出其它偏心距下的预应力简支梁自振频率，计算结果见图9。由表3和图9可知，一阶自振频率随偏心距的增大而增大，二者呈非线性关系。实际工程中由于要考虑钢筋保护层厚度、截面形状及整体受力等因素，偏心距改变范围比较小，而在这一范围内一阶频率与偏心距的关系则是呈线性变化的。

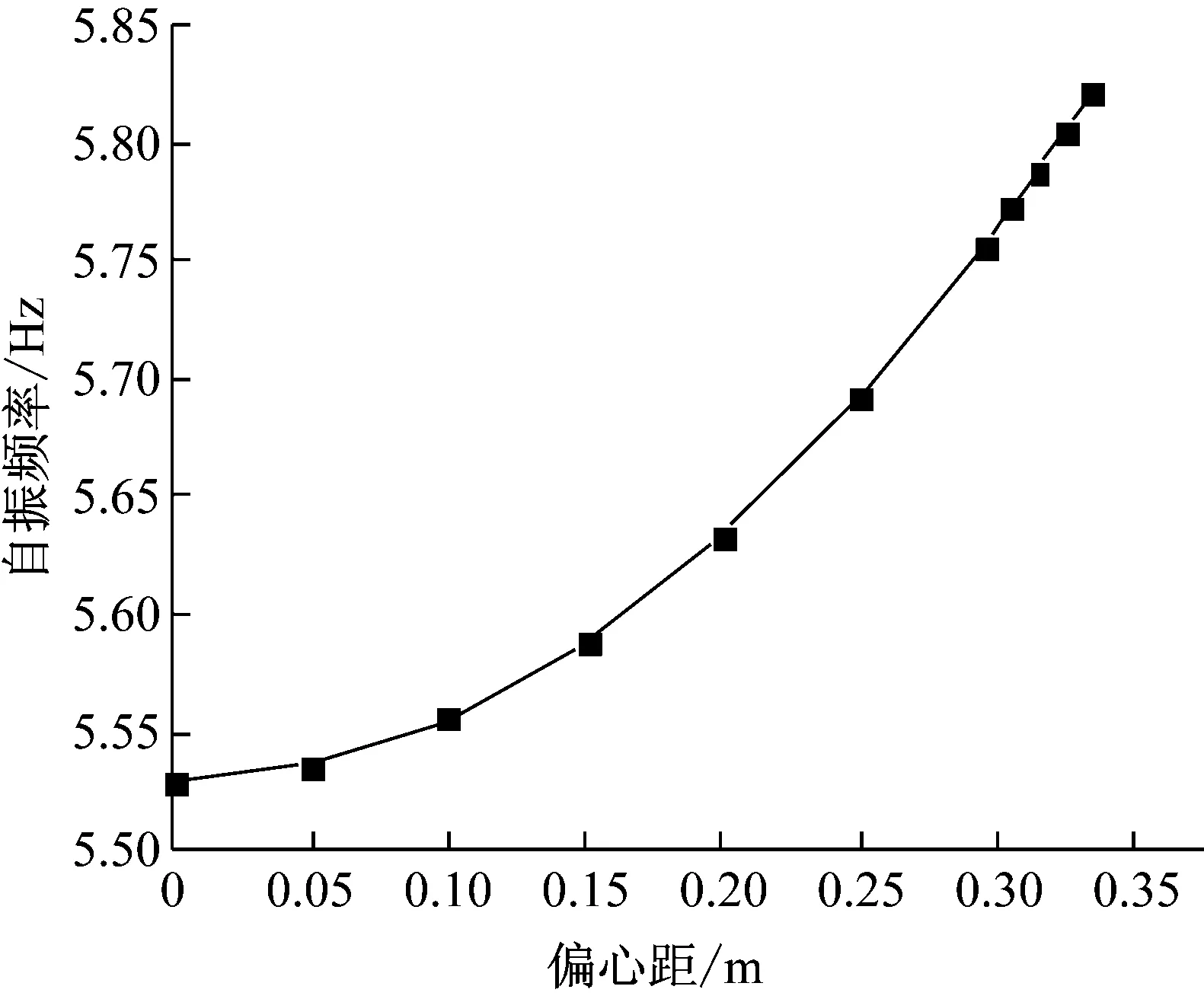
图9 不同偏心距对自振频率的影响Fig.9 The influence of different eccentricity on natural frequency

4 结 论

(1)采用本文提出的公式计算偏心直线不等长预应力筋简支梁的频率是合理、准确的，一阶和二阶频率计算值与试验值和有限元分析值吻合良好，对实际工程应用性强。

(2)当偏心距一定时，偏心直线不等长预应力筋简支梁自振频率随着钢筋预应力的增大而略有降低，钢筋预应力的大小对简支梁的自振频率影响较小。故实际工程中桥梁的预应力损失情况对其一阶频率影响很小。

(3)当预应力值一定时，自振频率随着偏心距的增加而增加，二者呈非线性关系；而实际工程中偏心距变化范围较小，二者呈线性关系。