基于SHPB技术的混凝土冲击弯拉惯性效应研究

陈徐东， 刘志恒， 陈 晨

(河海大学 土木与交通学院， 南京 210098)

混凝土结构在其工作过程中，除受到静力作用，还有可能受到冲击、爆炸等动力荷载的作用[1-4]。现有针对混凝土动态力学性能的研究主要是对其动态抗压强度的研究[5-6]，而对其动态抗拉强度的研究相对较少，主要原因是试验技术的缺陷以及理论知识的不完善。

弯拉强度是混凝土重要的力学性能指标之一[7-9]。现有的弯拉试验主要为静态的中点弯拉[10]和三点弯拉[11-12]。在混凝土动态力学性能的研究中，主要采用落锤试验技术[13-15]和分离式霍普金森杆试验技术(Split Hopkinson Pressure Bar, SHPB)[16-17]。落锤试验的应变率较低，而SHPB试验装置可以得到中高应变率下的混凝土的动态力学性能。如今，少有利用SHPB试验装置对混凝土这类准脆性材料的弯拉强度进行研究，主要原因是高速冲击过程中试件的支座部位难以受到力的作用[18]。Delvare等[19]提出了一种可以计算材料动态弯拉强度并与模拟结果相吻合的弯拉计算模型。Chen等[20]采用在普通SHPB装置上加套筒的方式来实现动态弯拉试验。

在冲击弯拉试验中，若干不确定的因素会影响试验结果，如试件惯性的影响。Bentur等[21-22]系统的研究了落锤试验存在的惯性力影响，其研究结果表明，惯性力占冲击力的比例较大。武明鑫[23]研究了落锤试验中去除惯性效应影响后真实DIF与应变率之间的关系，其结果能很好的符合欧洲CEB-FIP[24]规范。然而目前基于SHPB原理的弯拉试验并没有考虑惯性力的影响。基于此，本文利用改进的直径74 mm的SHPB装置，根据计算动态弯拉强度的无限长梁模型推导出试件断裂前的挠曲变形的有效长度的计算公式，并根据有效长度计算出惯性力。

1 试样准备

本试验采用的是40 mm×40 mm×160 mm的长方体混凝土试件。采用普通的三联模浇筑。配合比如表1所示，其中，水灰比为0.62，胶凝材料为普通硅酸盐42.5型水泥；细骨料为河砂；粗骨料为碎石，最大粒径为15 mm；水为实验室的自来水。为了增强拌合物的流动性，添加1.0%的聚羧酸减水剂。混凝土浇筑好后，覆盖养护24 h后拆模，然后在室温条件下的饱和氢氧化钠溶液中养护28 d。试件密度为2 500 kg/m3，28 d的标准立方体抗压强度为54.5 MPa。

2 静态强度计算

静态中点弯拉试验是在10 kN的万能试验机上完成的，其加载速率为0.05 kN/s，试验装置如图1所示。

图1 静态弯拉试验加载装置Fig.1 Static flexural test loading device

表1 混凝土的配合比Tab.1 The mixing proportion of concrete kg/m3

3 试验方法

用河海大学结构实验室的直径为74 mm的分离式Hopkinson 压杆加载试验装置进行试验。在入射杆和透射杆接触处安装套筒，将混凝土试件夹在两套筒之间，套筒两支座间的跨度为0.12 m。在试件和套筒接触处涂抹凡士林，减小摩擦。在试件中点处用AB胶黏贴加速度计，用于测量中点加速度，以便于计算出惯性力。如图2所示。本试验采用三种不同的冲击速度，每种速度下重复2～3次。

表2 静态弯拉试验结果Tab.2 Static flexural test results

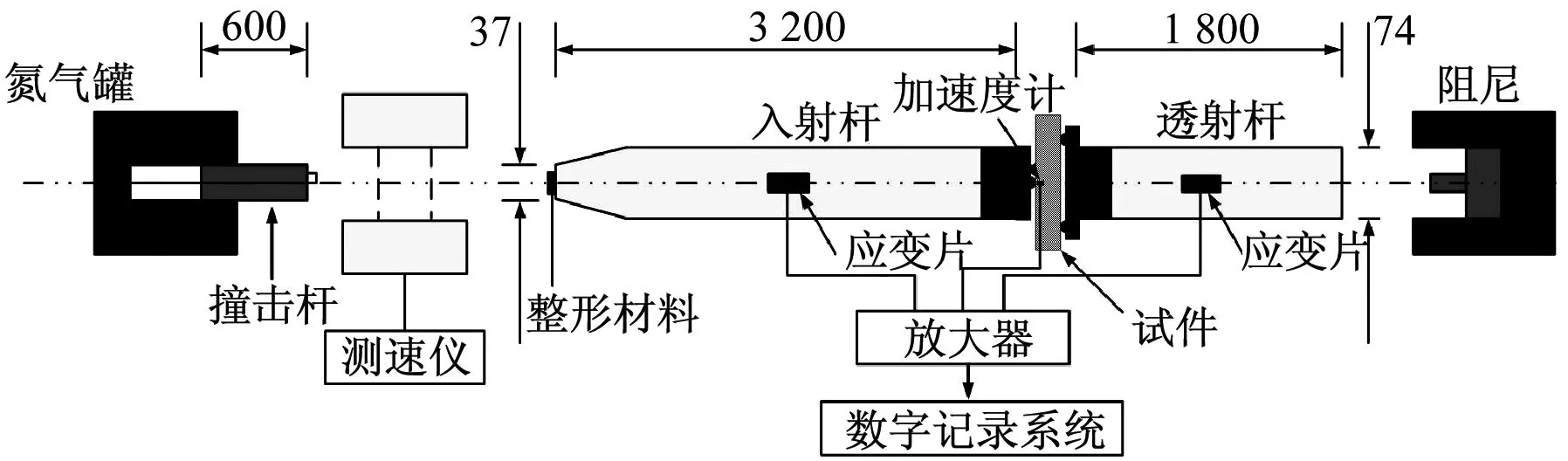
(a) 试验装置示意图 (mm)

(b) 试验装置实物详图图2 试验装置图Fig.2 Test device

由于SHPB试验装置满足一维弹性波理论，因此入射杆和试件之间的冲击力可以通过经典动量守恒和动力学方程计算得到

Fc(t)=-CBZB(εi(t)+εr(t))

(1)

Vc(t)=-CB(εi(t)-εr(t))

(2)

式中：CB表示杆的应力波波速，为5 100 m/s；ZB表示杆的材料阻抗，为172 097 kg/s；εi和εr分别表示入射杆上应变片记录的入射应变和反射应变。

4 试验结果分析

基于SHPB试验原理的动态弯拉试验，可以通过无限长梁模型推算出有效长度，然后结合实测加速度计算得惯性力。去除惯性力，即可得到实际冲击力，从而通过计算得到真实弯拉强度。下面对承受动力作用的混凝土实测数据进行分析。

4.1 加速度的数据分析

在撞击试验中，加载点处的垂直速度可以通过对所测得的加速度进行一次积分得到，而加载点处的挠度则可通过对加速度的二次积分得到。原始加速度图形是一个震荡和离散的图形。为了获得光滑和稳定的曲线来分析惯性力，运用频域分析技术，将原始加速度计测得的数据进行低通平均滤波，通带截止频率为500 000 Hz。

4.2 无限长梁模型

混凝土是一种准脆性材料，在动态弯拉试验中，试件从受力到破坏的过程很短，力还没有传递到支座处试件就已断裂，因此无法按常规计算弯拉强度的方法来进行计算。按Delvare等的思想，可以将整个试验过程等效成无限长梁模型，通过边界条件和初值条件得到动态弯拉强度的求解公式。

根据Bernoouli 提出的简化梁模型，只考虑梁的受弯作用而忽略剪力产生的扭矩。根据平截面假定，梁的挠度方程可以表示为

(3)

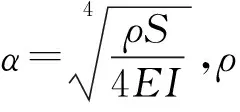
即使用无限长梁假设，梁中心位置应力的变化也不会受到支座影响。为方便使用采集到的数据，可以将问题简化为：一根很长的梁，根据所测量的数据可得到位移和作用力在撞击点的边界条件，还需要确定的是另外两个未知的边界条件，即X= 0处的旋转角ψ(0,t)和弯矩M(0,t)，示意图见图3。根据边界条件可以得到

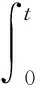
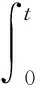
(4)

式中：ω表示挠度;x表示试件上某一位置距离试件中点的距离;t表示试件断裂时间。此外

由此可得在x= 0处的旋转角

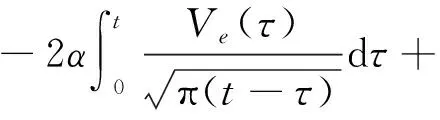
(5)

(6)

由于在x= 0处，ψ(0,t) = 0，故可以得到断裂发生前弹性阶段时入射杆与试件接触端的冲击速度和冲击力之间的关系式

(7)

通过式(6)、(7)可求得在试件未产生裂缝时的弯矩

(8)

根据材料力学可得最大应力为

(9)

最大应变率为

(10)

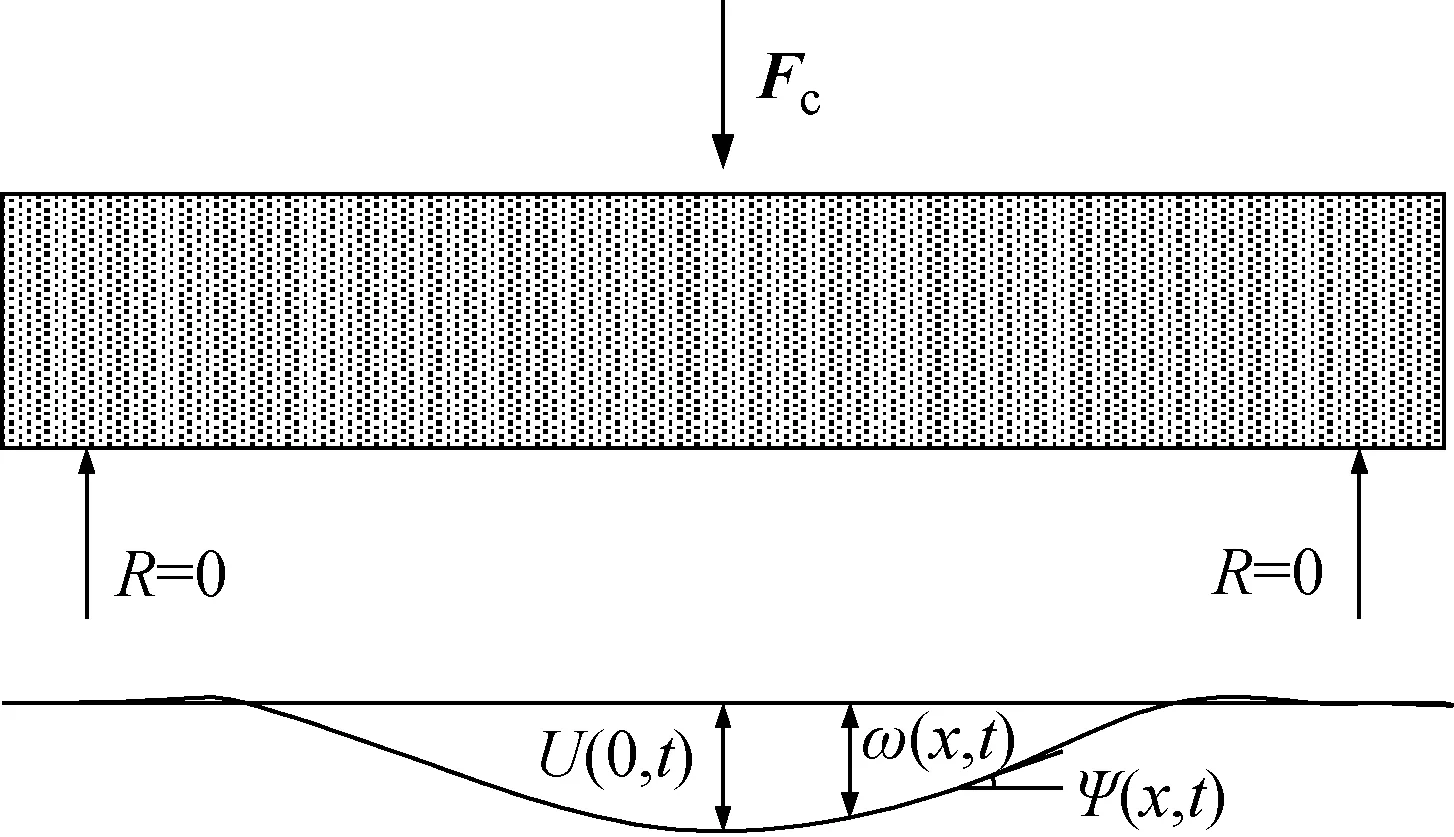
图3 长梁模型原理示意图Fig.3 Long beam model principle diagram

4.3 有效长度的计算

在冲击弯拉试验中，支座受到的力R= 0，故在断裂前发生变形的试件长度无法得知，但根据无限长梁模型给出的关系，该长度可以计算得到。因此将试件在冲击弯拉试验中发生挠度变形部分的长度定义为有效长度。

由于

(11)

由式(6)、(7)可得

(12)

(13)

根据式(4)、(13)可得

2G1(t)=G2(t)

(14)

将式(14)代入式(4)得

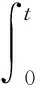
(15)

当t达到最大时，ω(x,t)=0，即

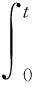
(16)

由于t很小，故上式可简化为

G1(t-τ)Ω1(x,t)-3G1(t-τ)Ω2(x,t)=0

(17)

Ω1(x,τ)=3Ω2(x,τ)

(18)

将式(6)、(7)代入式(18)得到

(19)

(20)

(21)

由于x∈(0, 0.06m)，所以

(22)

式中：l表示有效长度；t表示试件的断裂时间。

4.4 惯性力分析

惯性力是指当物体有加速度时，物体具有的惯性会使物体有保持原有运动状态的倾向，而此时若以该物体为参考系，并在该参考系上建立坐标系，看起来就仿佛有一股方向相反的力作用在该物体上令该物体在坐标系内发生位移，因此称之为惯性力。

Bentur等和Banthia等研究了落锤试验的中点弯拉试验，指出实测荷载包括了惯性力和变形力两部分。

Pt(t)=Pd(t)+Pi(t)

(23)

式中：Pt表示试件承受的所有的力；Pd表示广义弯曲力；Pi表示广义惯性力。

混凝土的变形过程一般分为两个阶段，即弹性变形阶段和损伤开裂阶段。根据弹性梁理论，对于弹性变形阶段，可以将其挠度分布曲线考虑成三次曲线；对于损伤开裂阶段，一般将挠度曲线考虑成折线段。Wu等[25]在考虑落锤实验中的惯性力时，为简化计算，将整个变形过程中的挠度曲线考虑成三次曲线，以此根据虚位移原理得到了惯性力的计算公式。

在SHPB动态弯拉试验中，仅仅考虑试件的弹性极限状态，因此可以采用非线性的惯性力的计算模型，惯性力计算原理示意图如图4所示。

(24)

等效惯性力表达式为

(25)

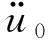
因此最大应力为

(26)

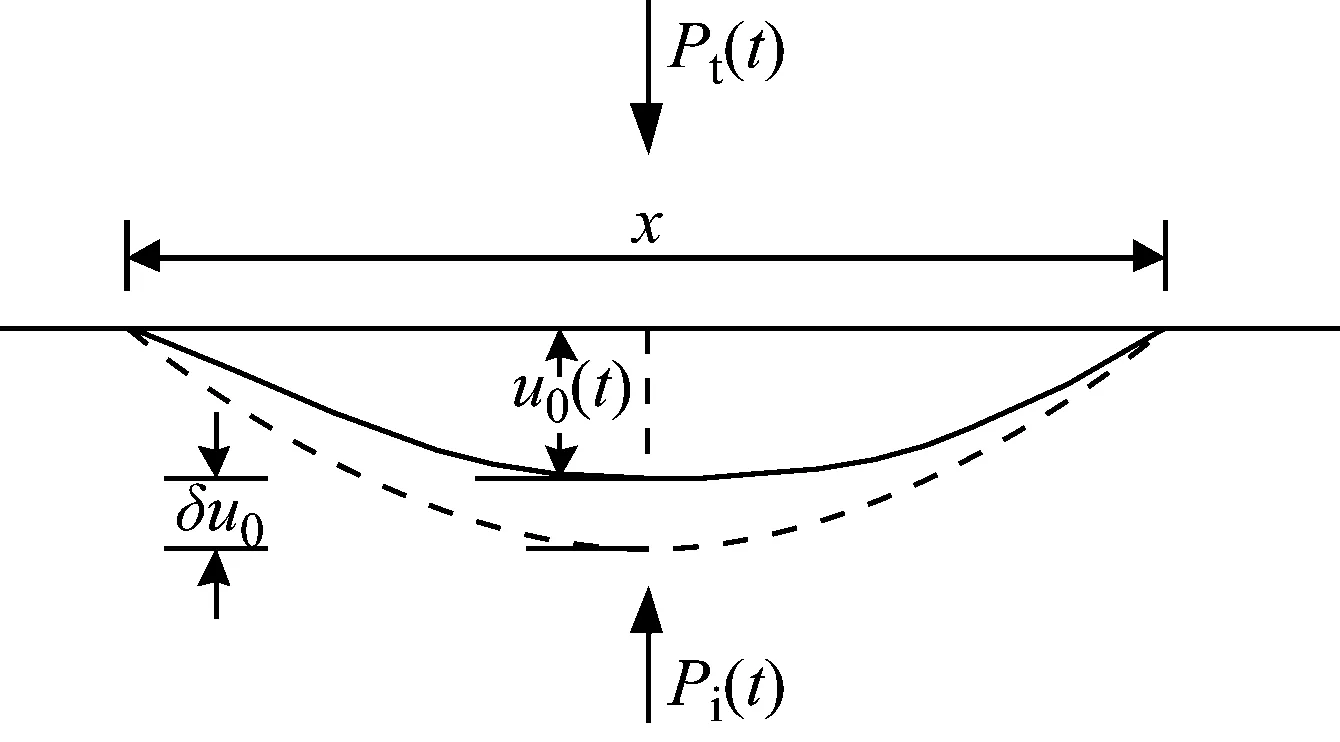
图4 惯性力计算原理示意图Fig.4 Inertial force calculation principle diagram

5 试验结果

在动态弯拉试验中，采用不同的冲击速度即可获得不同的应变率，进而研究不同应变率下混凝土的强度变化。表3展示了不同冲击速度情况下的试验结果。在每种工况测试了2～3个试件。

通过表3，可以发现在基于SHPB试验原理的动态弯拉试验中，试件的有效长度随着应变率的提高而增大。图5展示了试件所受冲击力的大小，其结果显示随着子弹撞击速度的增加，冲击力的峰值力随之增大。图6所示的是试件所受到的惯性力与冲击速度的关系，惯性力也随着冲击速度的增大而增大。惯性力和冲击力有一定的对应关系，冲击力越大，惯性力越大。

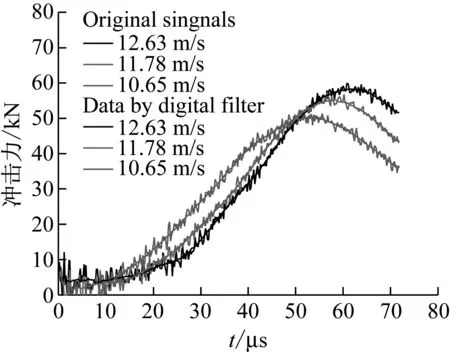
图5 不同冲击速度下，冲击力-时间关系曲线图Fig.5 The impact-time curve under different impact speed

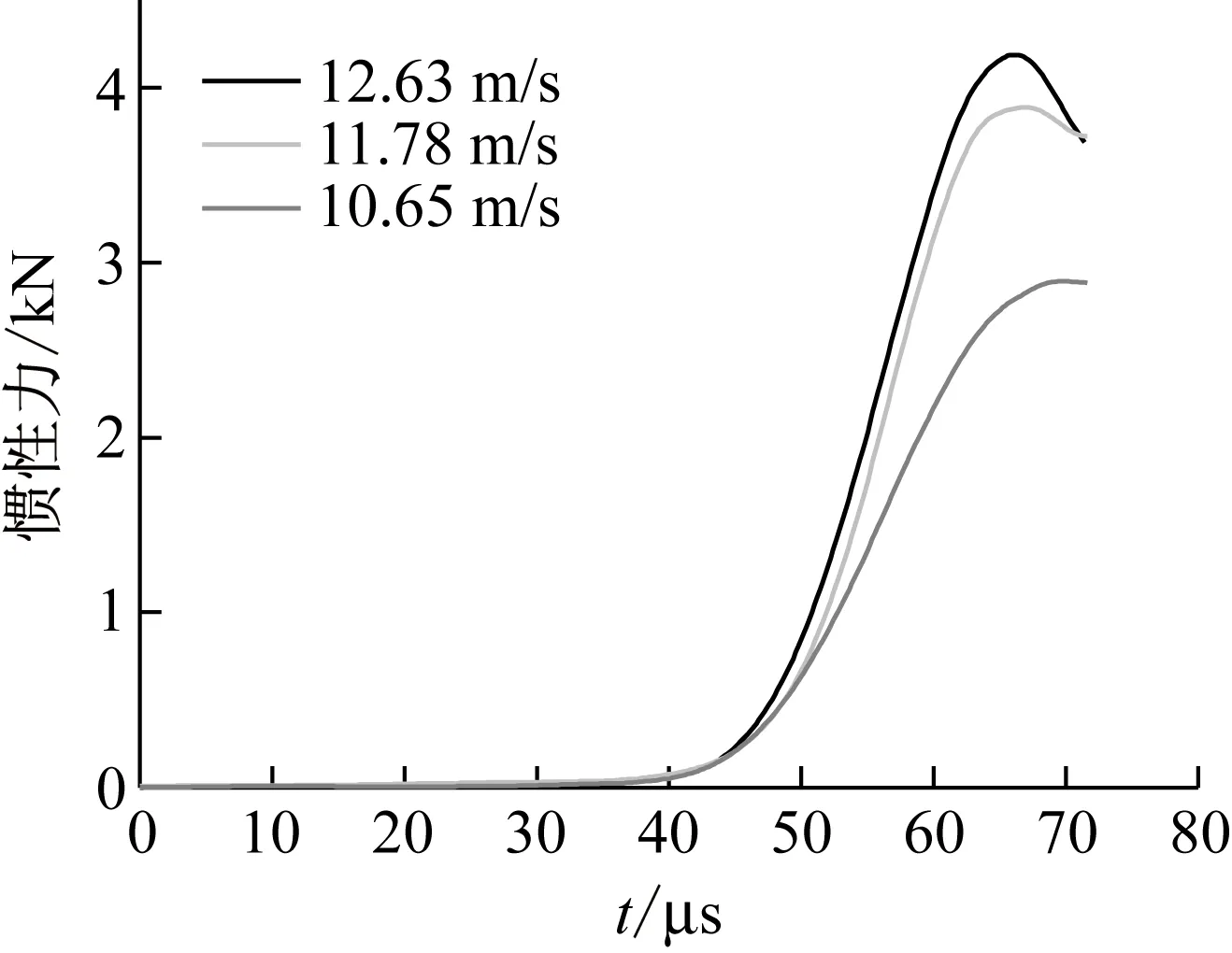
图6 不同冲击速度下，惯性力-时间关系曲线图Fig.6 The inertia force-time curve under different impact speed

如前所述，试件沿着撞击方向的挠度可以通过对加速度进行二次积分得到。如图7所示，挠度随着冲击速度的增大而增大。由图8可以看出随着冲击速度的增大，试件所受到的冲击力增大。

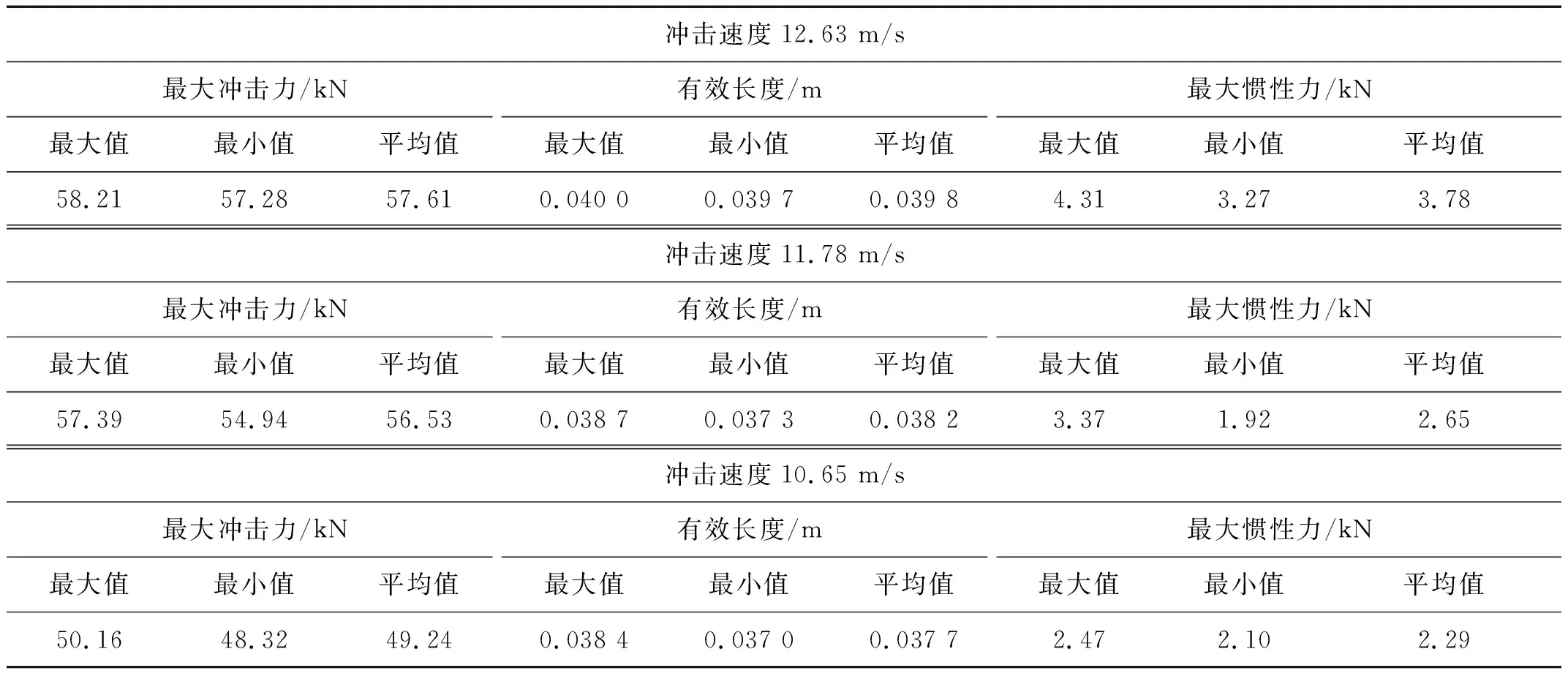
表3 不同冲击速度下最大冲击力、有效长度和最大惯性力的大小Tab.3 Biggest impact, effective length and largest inertia force under different impact speed

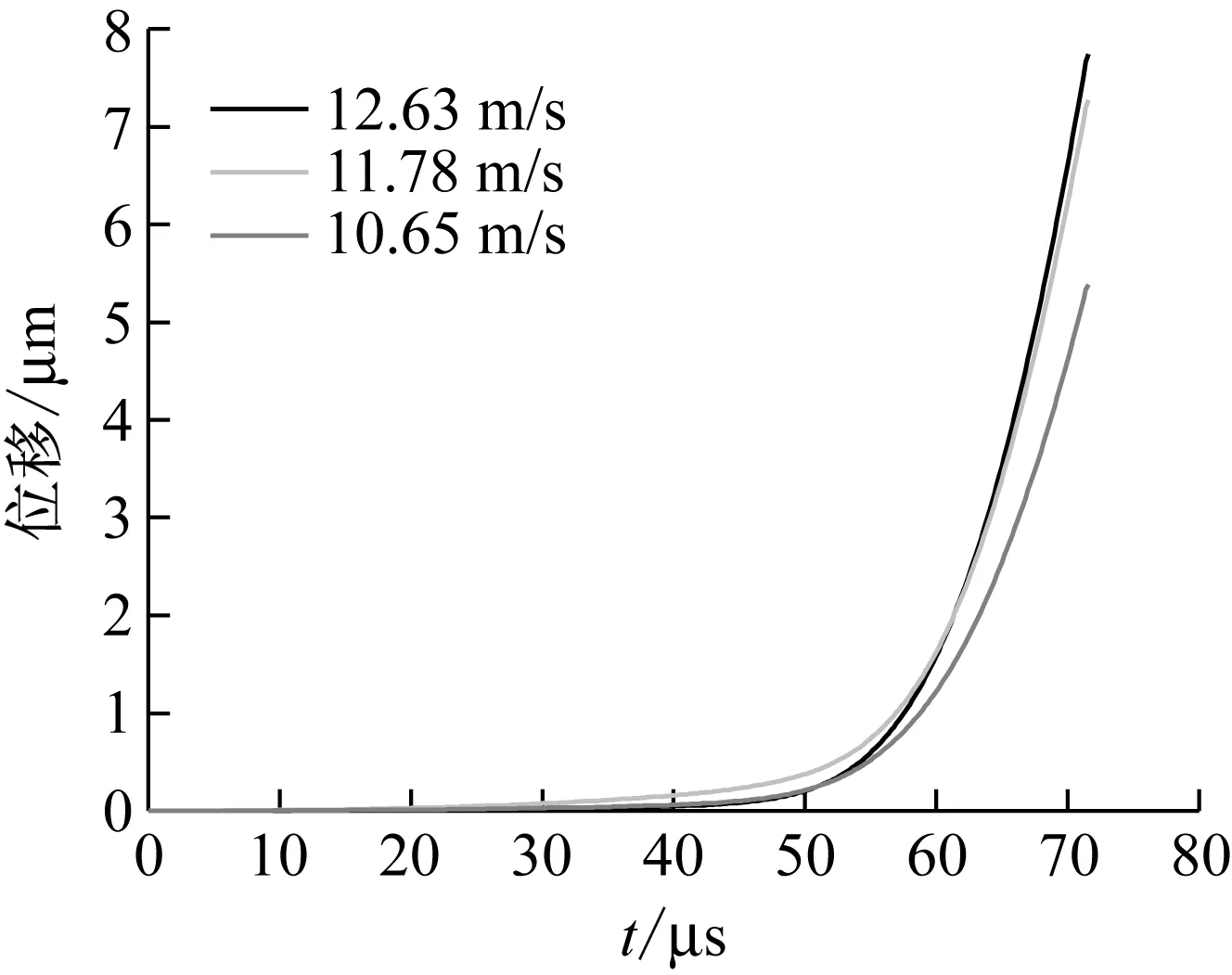
图7 不同冲击速度下，位移-时间关系曲线图Fig.7 The displacement-time curve under different impact speed

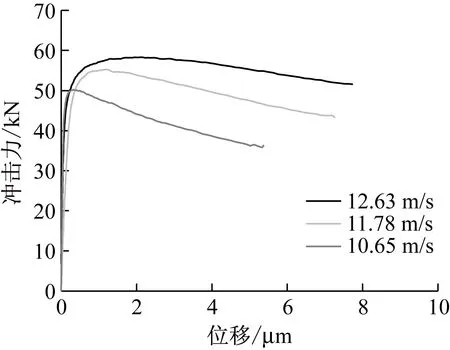
图8 冲击力与位移关系图Fig.8 The impact force-displacement curve

5.1 应变率的影响

众所周知，混凝土的动态抗压特性可以通过动态抗压强度和静态抗压强度的比值来体现，即动态强度提高因子(DIF)。目前很多研究表明DIF能够准确描述混凝土材料的率敏感性。在本文中，DIF的计算公式为

(27)

式中:σd表示的是混凝土试件所受冲击力中除去惯性力部分的有效强度;σs表示混凝土试件的静态受弯强度。

根据欧洲CEB-FIP对混凝土动态强度提出的关系式模型，并考虑了混凝土静态强度的影响，提出了最高应变率为30 s-1的混凝土DIF公式

(28)

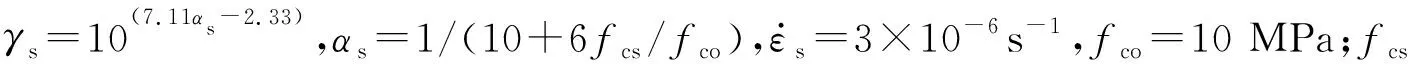
通过图9可以得到DIF与应变率之间的关系。经试验发现冲击速度越大，应变率也越大，且随着应变率的增加，其DIF增加，能很好的满足欧洲CEB-FIP规范给出的模型公式。

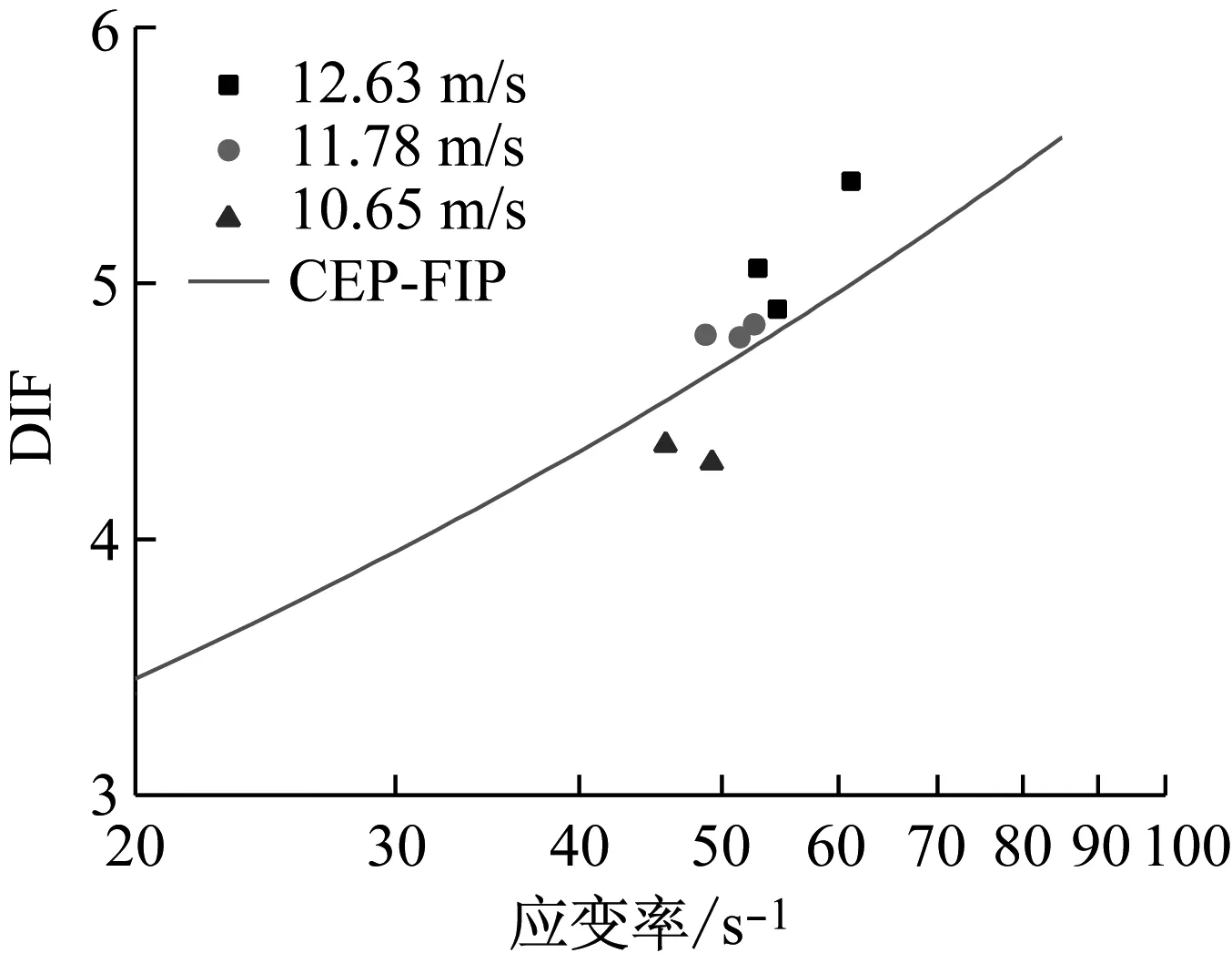
图9 DIF与应变率关系图Fig.9 DIF - strain rate curve

5.2 能量

当入射杆冲击混凝土试件时，入射杆上的部分能量传递给了混凝土试件并使得试件断裂。通过力与位移之间关系曲线，积分可以得到相应的能量。在不同冲击速度下入射能和惯性能的大小，见表4。

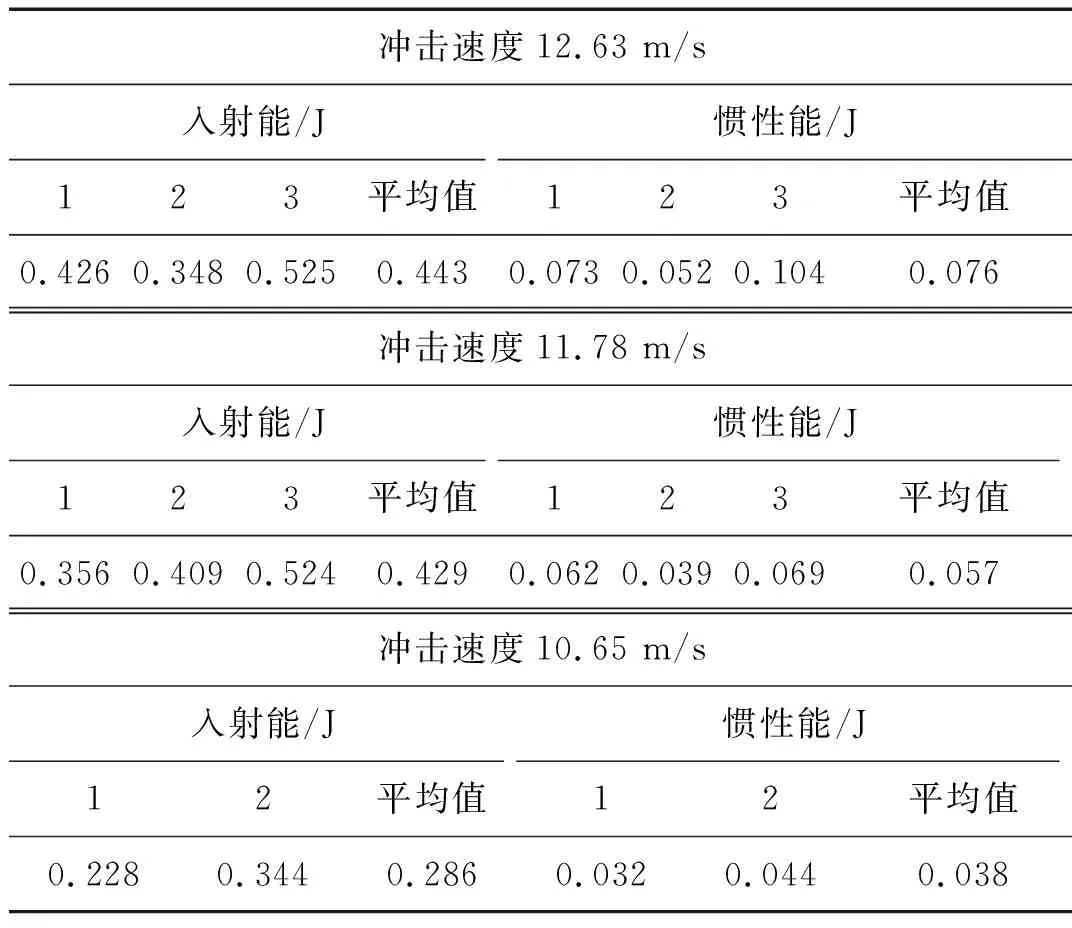
表4 不同冲击速度条件下入射能及惯性能的大小Tab.4 The incident energy and inertia under the condition of different impact velocity

通过图10和图11的对比，可以看出当入射能显著增加时，惯性能也在明显提高。

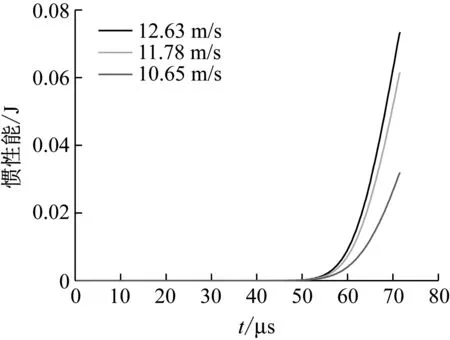
图10 惯性能与时间关系图Fig.10 Inertia energy-time curve

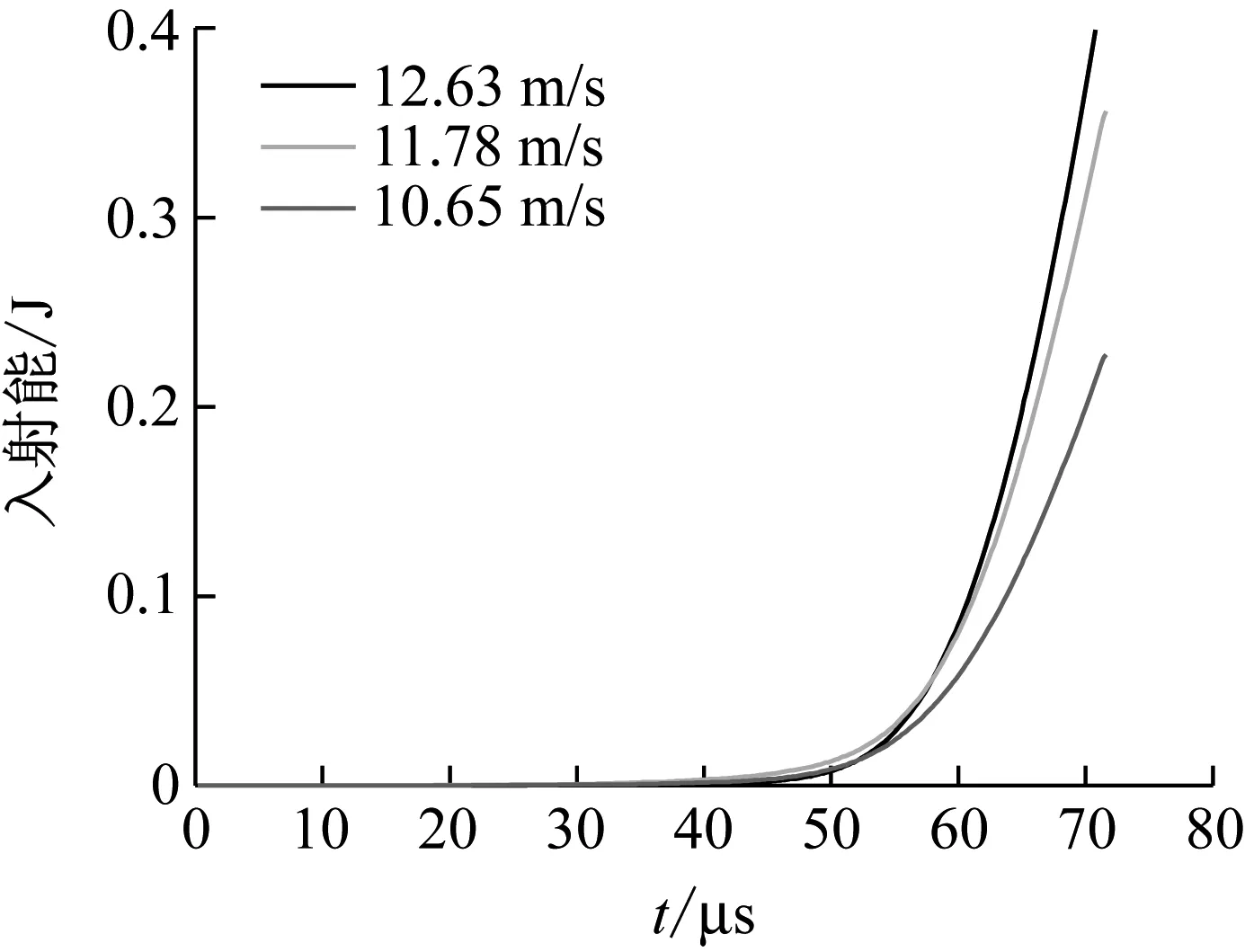
图11 入射能与时间关系图Fig.11 Impact energy-time curve

6 结 论

本试验将Hopkinson 压杆试验装置与加速度计结合，得到了高应变率试验中惯性力，分析了不同撞击速度条件与冲击力，惯性力以及位移的关系，并获得以下结论：

(1) 装在试件上的加速度计可以测量试件在断裂过程中的加速度，并以此推算出试件所受惯性力及其位移；

(2) 在去除惯性力之后的有效应力的DIF在4～6时，其对应的应变率在45～70 s-1，DIF随着应变率的增大而增大，说明在霍普金森弯拉试验中惯性力对试件有一定的影响；

(3) 在中高应变率条件下，弯拉试件在受撞击断裂时只在有效的长度内受惯性力作用，并且当入射杆冲击试件，试件断裂之后撞击到透射杆上，一部分入射能转换为试件的动能。