新课改背景下初中数学作业设计探析

舒国莲

(广东省深圳市龙岗区平湖中学，广东深圳 518111)

引 言

在新课改要求必须为初中生减轻作业负担的背景之下，数学教师们在为学生设计数学作业时，不能仅仅按照自己的想法随心所欲进行设计，而应在遵循新课改的相关原则下，结合学生的实际情况设计数学作业，以保证学生能充分吸收理解所学知识[1]。

一、新课改下数学作业设计应结合教学重难点学习内容，目标明确

教师设计的数学作业除了要紧紧围绕课程标准，并与所讲授的知识息息相关外，还要在给学生减负的同时，主要在所设计的数学作业中,将学校的教育理念和作业本身的价值体现出来。如数学教学中遇到的难题，教师在设计作业时要将难题进行适当的分解，使学生能由浅至深地完成作业。

以北师大版的初中数学为例，在初中数学作业中，各种几何图形一直是让学生头疼的重点难点。如在九年级下册第一章“直角三角形的边角关系”中第4小节“解直角三角形”这一数学知识学习的数学作业设计中，直角三角形课程的重点一般是“勾股定理，30°，45°，60°角的三角函数值、两锐角互余或互补、锐角三角函数解直角三角形，并将直角三角形的相关知识运用到实际问题中”，难点在于大多数初中生无法以多种角度运用解直角三角形方法解答以三角函数为题设计的三角综合题。因此，教师在设计初中数学作业时，应结合教学过程中出现的重点难点，设置出“如图所示，在梯形ABCD中，AB//DC，DA=AB=BC=1，CD=2，点P在三角形BCD内运动，则求向量AP和向量BD的取值范围，并指出其自变量的取值范围。”等能突出作业设计的针对性和目的性的题目，切实提高学生的数学水平。

二、新课改下数学作业设计应结合实际运用问题，适量减负

在题海战术的压迫下，学生短时间内的数学成绩虽然有所提高，但从初中生的长远发展来看，题海战术的实施只会扼杀学生对数学的热情和主观能动性，抹杀学生在初中数学上的思维和灵感，还会引起学生对初中数学作业的厌烦心理。因此，初中数学教师在设计数学作业时应尽量遵循适量性原则，题目贵精不贵多，通过少而精的典型题目帮助学生更好地学习数学。

如北师大版初中数学八年级下册第四章“分解因式”中的“运用平方差公式分解因式”这一课程内容，教师可以以三道较为典型的题目作为学生的课后作业。

(1)若2x3+3x3+mx+1为x+1的倍式,则m＝__________ 。

(2)因式分解下列各式：①4x2-25，②x2-4xy+4y2；③利用(1)(2)之方法求a2-b2+2bc-c2。

三、新课改下数学作业设计应结合当天所学知识，层次分明

世界上没有完全相同的两片树叶；同样地，世界上也没有完全相同的两个人。因此，教师在设计初中数学作业时，就必须考虑到不同学生间不同层次的认知水平、理解能力和接受能力等因素，因材施教，进行多层次问题的设计满足不同学生的作业需求。

如在北师大版初中数学八年级上册第二章关于实数练习的作业设计中，教师可以设计由易至难、由浅及深的三道题目作为学生的作业，按步骤引导学生独立完成数学作业。使学生能从中学到知识，并将这些知识带到日常生活中。如以下题型：

(1)下列说法不正确的是（ ）。

A.-1的立方根是-1 B.-1的平方是1

C.-1的平方根是-1 D.1的平方根是±1

(2)-27的立方根与9的平方根之和为（ ）。

A.0 B.9 C.-9 D.0或-9

(3)已知某数有两个平方根分别是a+3与2a-15,求这个数。

四、新课改下数学作业设计应结合拓展延伸内容，开放思维

初中教师在设计数学作业时，应注意要特别设计有助于学生发散思维、创新发展的开放性题目，激发他们的主观能动性，让他们学会自主学习和思考，灵活运用所学知识解答所遇到的难题，并在这些锻炼中不断超越自我[2]。

如在二次函数的练习中，为加深学生对二次函数中函数图像和a、b、c之间关系的认识和理解，教师可以在设计初中数学作业时，设计一道同时具有开放性与探究性的题目，让学生通过探究寻找不同的解决方法。如以下题目：

(1)图1为二次函数y=ax2+bx+c的图像，则abc，b2-4ac，2a+b，a+b+c这四个式子中，值为正数的有（ ）

A.4个 B.3个 C.2个 D.1个

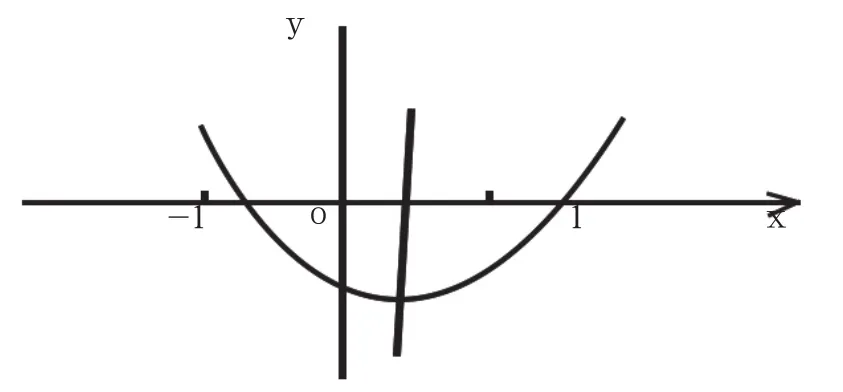
图1

图2

（2）如图2，抛物线y=-54x2+174x+1与y轴交于点A，过点A的直线与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C（3，0）。则①动点P在线段OC上，从原点O出发以每秒一个单位的速度向C移动，过点P作x轴的垂线，交直线AB于点M，抛物线于点N，设点P移动的时间为x秒，线段MN的长为s个单位，求s与x的函数关系式；②在①的条件下（不考虑点P与点O、点C重合的情况），连接CM和BN，四边形BCMN能否为平行四边形？若能，求出点P的坐标；若不能，请说明理由。

结 语

总之，在新课改的要求下，通过合理的作业设计，适当适量地为学生布置目的明确、层次分明的数学作业，使他们能够发挥其对数学学习的主观能动性，为他们以后的数学学习打下良好的基础。