行列式的计算方法与解析研究

徐建中

（亳州学院，安徽 亳州 236800）

1 前言

行列式的计算在高等代数学习中起着举足轻重的作用，最常用的是利用行列式的性质和展开定理，进行计算.但是对于具体的题目需根据其具体特点采用不同的计算方法，本文主要采用7种方法归纳总结了行列式的算法.下面主要针对具有不同形式的行列式利用不同的方法进行计算加以说明.

2 计算方法及解析

2.1 化三角形法

例1 计算n阶行列式Dn的值，

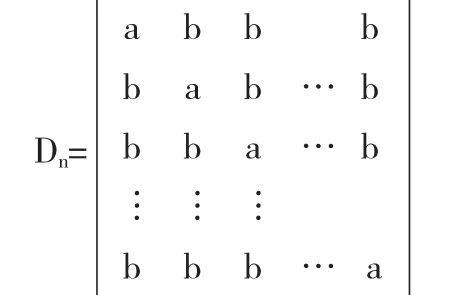
解 这个行列式的特点是每一列有一个元素a,其余n-1项个元素为b,根据行列式其一性质（若行列式的某一行元素乘以同一个数后加到另一行的对应元素上去，则行列式的值不变.），把第二行加到第一行，d不变，再把其余各行也加

(-1)乘第一列后分别加到其余各列，则有：

2.2 提取公因式法

2.3 利用拉普拉斯（Laplace）定理法

例3 计算2n阶行列式

解 根据拉普拉斯定理，在d2n中按第1行与第2n行展开得

右端2n-2阶行列式的结构完全与d2n一样，于是

在与dn同型的2n-2阶行列式d2n-2中，按第一行与第2n-2行展开，有

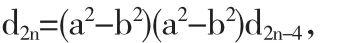
如此继续下去，可得

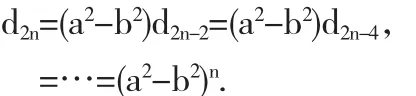
2.4 利用范德蒙(Vandermonde)行列式法

例4 计臬n阶行列式

解 从dn中第n-1行开始到第1行止，每行乘以（-an）加到下一行，得

按第n列展开有

提取各列因子后得

右端行列式结构与dn完全一样，用dn-1表示，于是

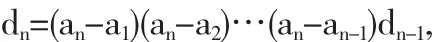
这个式子称为递推关系式.对dn-1同样的方法可得

依次类推，得

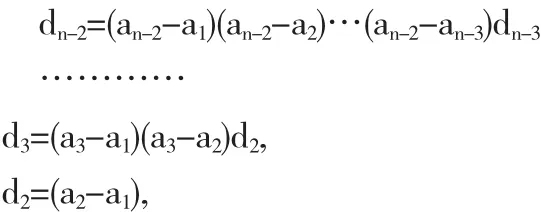
从而有

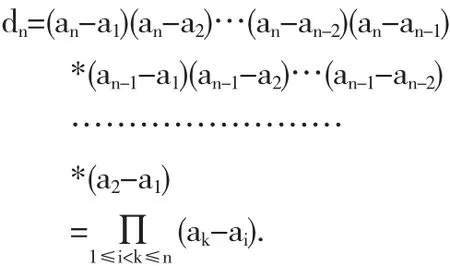
这里∏是连乘符号，上式表示满足1≤i≤k≤n所有因子(ak-ai)的连乘积.

2.5 特征根法

例5 已知I-A的特征根之模长均小于1，

证明：0＜|detA|＜2n.

证明 首先A没有零特征根，否则存在可逆阵P，使得

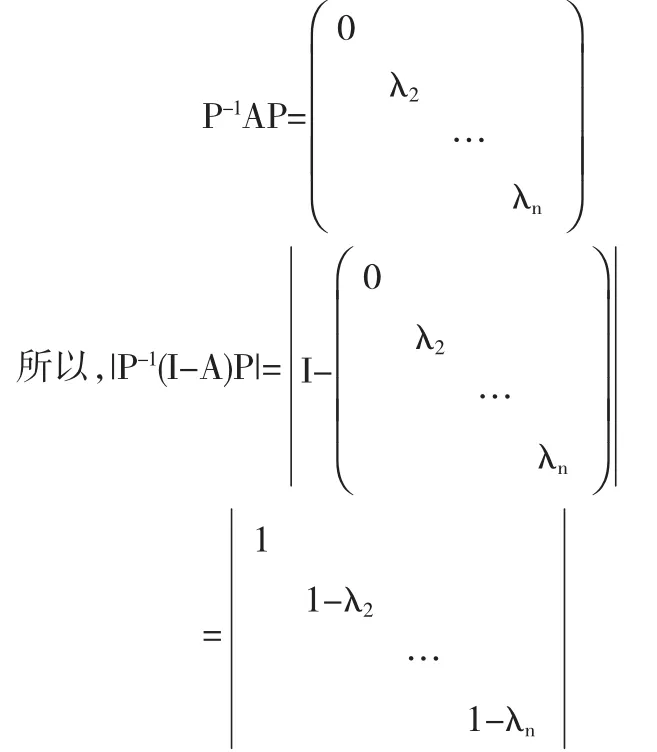
所以，1为I-A的特征根矛盾.

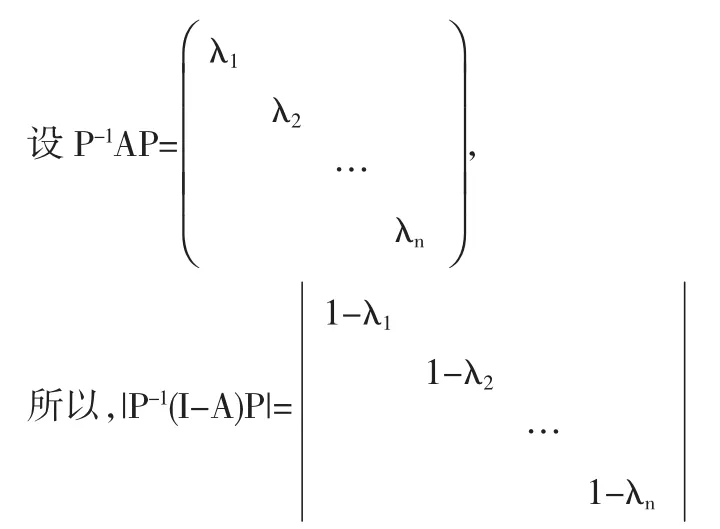
所以，|1-λi|＜1 即 1＞|λi|-1 即 |λi|＜2,所以，|λ1λ2…λn|＜2n即0＜|detA|＜2n.

2.6 数学归纳法

例6 用数学归纳法证明：

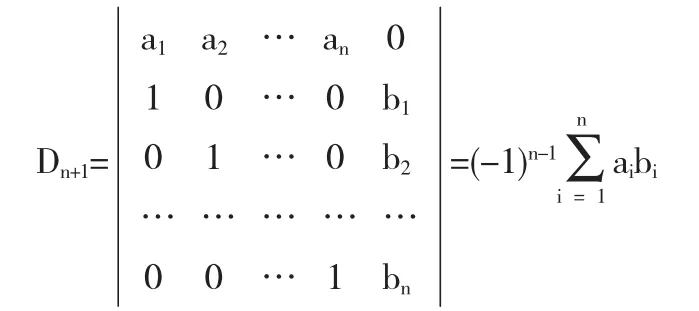
假设n=k时，命题成立，要证n=k+1时，等式成立.

b按最后一行展开得：

注：本题可按行列式定义展开，也可按行或者列展开，还可将第i+1行(i=1,2,…,n+1)乘以(-ai)都加到第1行，再按第1行展开.同样可证得此式.

2.7 利用行列式乘法规则

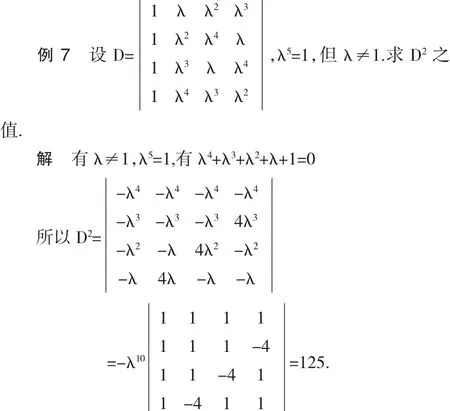
3 总结

总之，计算行列式的方法很多，本文只归纳总结了7种方法.理解和掌握以上7种方法，遇到一些具有以上形式的行列式就能计算出它们的值，此外还会有其他形式的行列式，可以通过变相转换的方法转化为这几种方法来计算.