“面面俱到”——剖析斜面相关问题

冯 兰

(江苏省吴江中学 215200)

高中物理中的力学问题许多都是以斜面为载体，问题的呈现离不开斜面，所以说斜面是高中物理中的重要模型.对与斜面相关的问题做一个具体的总结非常有必要，有利于学生更为系统的掌握与斜面相关的知识，提高学生解决与斜面相关问题的能力.

一、细绳结合斜面问题

对于斜面上的物体，如果只受到平行于斜面的拉力或者推力的作用，都可以看作是通过细绳对物体进行牵引，这类问题可以归结为细绳与斜面结合问题，一般通过整体法以及隔离法可以解决相关问题.

图1

例1 如图1所示的倾角为θ，质量为M粗糙斜面上，放置质量为m的物体A，用平行于斜面的细绳牵引物体A，已知细绳的拉力为F，使物体沿斜面做加速度为a的匀加速直线运动，此时斜面静止.求地面对斜面的支持力N和摩擦力f的大小.

解析对有物体A和斜面组成的整个系统来受力分析，受到外力有：重力=m+Mg，拉力=F，地面的支持力=N，地面所受摩擦力f.将加速度a沿水平和垂直两个方向分解为：ax=acosθ，ay=asinθ，由牛顿第二运动定律知，整个系统水平方向合力向右，且Fcosθ-f=mamx+MaMx,这里amx=ax,aMx=0，得到：Fcosθ-f=macosθ；同时受力分析可得整个系统竖直方向合力向上，且Fsinθ+N-m+Mg=mamy+MaMy，这里：amy=ay,aMy=0，得到：Fsinθ+N-m+Mg=masinθ.由以上式子可得：f=Fcosθ-macosθ，N=m+Mg-Fsinθ+masinθ.

点拨以上题目当中分别对系统整体的竖直方向和水平方向进行受力分析，分析的过程思路清晰，通过整体受力分析的方法，达到了简化计算的目的，提高了解题效率.

二、滑轮结合斜面问题

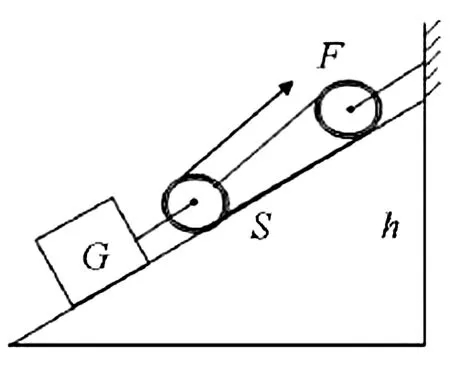
图2

滑轮组与斜面的组合，组成双机械模型，比起细绳与斜面结合问题，这类问题多了一个难点，即滑轮组对问题的解决造成干扰，但是只要抓住问题的本质，这类问题的解决也不会非常困难，通过下面的例题可以对滑轮结合斜面问题有一个具体了解.

例2 如图2所示，物体的重力G=2000N，斜面的长度S=5m，高度h=3m，已知斜面与滑轮组装置的机械效率为80%，如果将重物沿着斜面方向以0.2m/s的速度向上拉动，求：(1)所需要的拉力F是多大？(2)机械的总功率是多少？

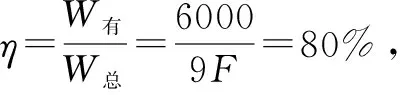
点拨本题中的机械装置是斜面与滑轮组的组合，该装置的目的是将物体从斜面的底部运到斜面的顶部，这种双机械模型在实际生活中有着重要的应用，虽然总的机械效率有所降低，但是滑轮的使用减小了所需要的拉力.

三、弹簧结合斜面问题

轻弹簧与斜面相结合的问题在高中物理中也是一种非常常见的题型，一般都是弹簧的一端连接着物体，另一端用相应的拉力来拉弹簧，本例介绍一种新的题型，即弹簧的两端同时连接着物体，根据弹簧拉伸和压缩时的两种状态进行受力分析.

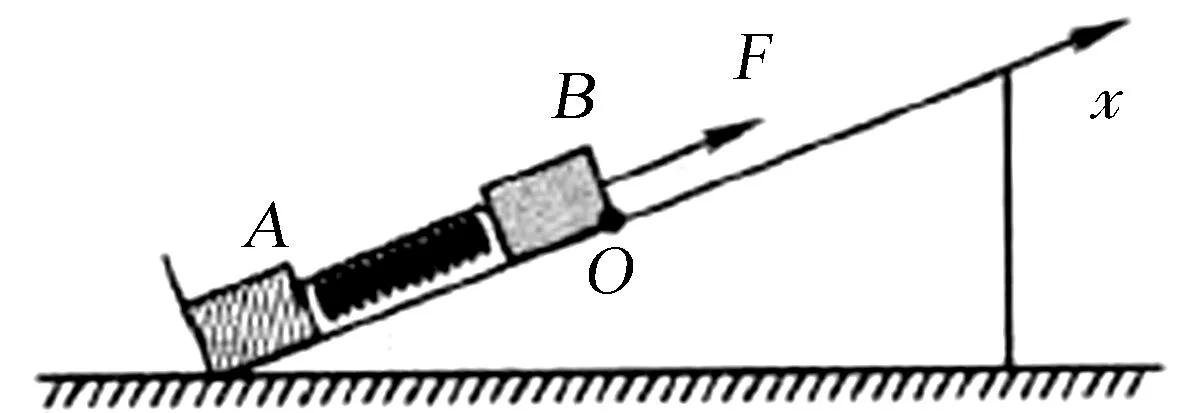
图3

例3 如图3所示，处于静止状态、质量相同的A、B两个物体由轻弹簧相连接，光滑斜面的底端固定着一个垂直于斜面的挡板，现在用平行于斜面的力F拉动物体B做加速度为a的直线运动，如果用B物体的初始位置作为坐标原点、沿着斜面向上方向建立Ox坐标轴，设斜面的倾角为θ，请求出当物体A离开挡板之前(弹簧一直处于弹性限度内)，外力F和挡板对物体A的作用力随B物体的位置坐标x的变化关系式？

解析设最初始状态时弹簧的压缩量为x0，即kx0=mgsinθ，对于物体B，当弹簧压缩时，F+k(x0-x)-mgsinθ=ma，由于kx0=mgsinθ，所以F=ma+kx；当弹簧拉伸时，F-k(x-x0)-mgsinθ=ma，同理可得F=ma+kx.对于物体A，当弹簧压缩时，N=mgsinθ+k(x0-x)，即N=2mgsinθ-kx；当弹簧拉伸时，N+k(x-x0)=mgsinθ，即为N=2mgsinθ-kx.

点拨在弹簧拉伸和压缩时，A、B两个物体的受力情况完全不同，这也是本题需要注意的地方，所以本题的关键在于隔离法的使用，通过隔离法进行受力分析可以非常快速的解决问题，而且思路简单明了，效率大大提高.

综上所述，斜面问题的解决离不开相关的物理知识，无论是整体法还是隔离法，以及牛顿运动定律的相关知识，对于解决斜面相关问题都是极为重要的，所以学生在平时的复习中应当注意这些知识的积累，认真思考、善于归纳总结，只有这样才能在高考中取得好成绩.