立体几何复习和解题策略

郑加金

(福建省莆田市仙游县华侨中学 351200)

立体几何问题是高考的必考点，也是考查的重点内容，高中数学的立体几何对核心素养的考查是很全面的，既有很强的抽象能力、逻辑推理能力又有数学建模、直观想象和运算分析能力.立体几何一直让很多学生觉得不好学.在复习中如何让复杂和枯燥的几何图形变得形象生动，让学生打开空间思维想象能力，在具体的解决问题中能游刃有余、灵活变通.在立体几何专题复习中，整理了部分立体几何题型，总结出一些解题策略.

一、熟悉文化、拉近距离

透过传统文化的壳，看到数学的本质，帮助学生熟悉，消除恐惧感，陌生感，冷静分析.

例题1 《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马；将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥P-ABC为鳖臑，PA⊥平面ABC，PA=AB=2，AC=4，三棱锥P-ABC的四个顶点都在球O的球面上，则球O的表面积为( ).

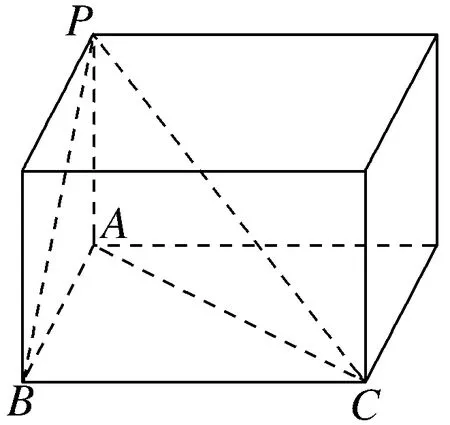
A．8π B．12π

C．20π D．24π

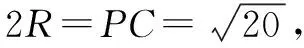
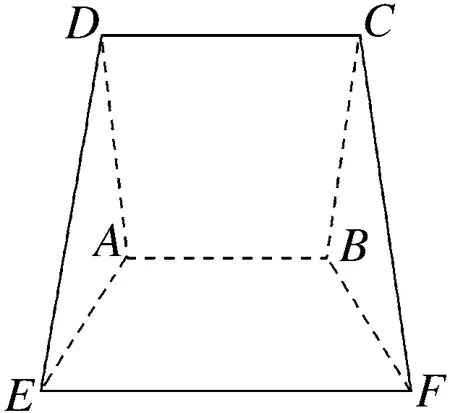
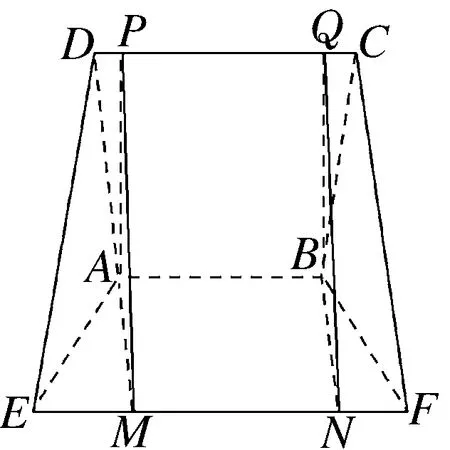
例题2 中国古代数学名著《九章算术》中记载：“今有羡除”．刘徽注：“羡除，隧道也．其所穿地，上平下邪．”现有一个羡除如图所示，四边形ABCD，ABFE，CDEF均为等腰梯形，AB∥CD∥EF，AB=6，CD=8，EF=10，EF到平面ABCD的距离为3，CD与AB间的距离为10，则这个羡除的体积是( ).

A．110 B．116 C．118 D．120

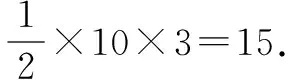
二、立体几何解答题建模、建系策略

立体几何解答题的基本模式是论证推理与计算相结合，以某个几何体为依托，分步设问，逐层加深.解决这类题目的原则是建模、建系.建模——将问题转化为平行模型、垂直模型、平面化模型及角度、距离等的计算模型；建系——依托于题中的垂直条件，建立空间直角坐标系，利用空间向量求解.

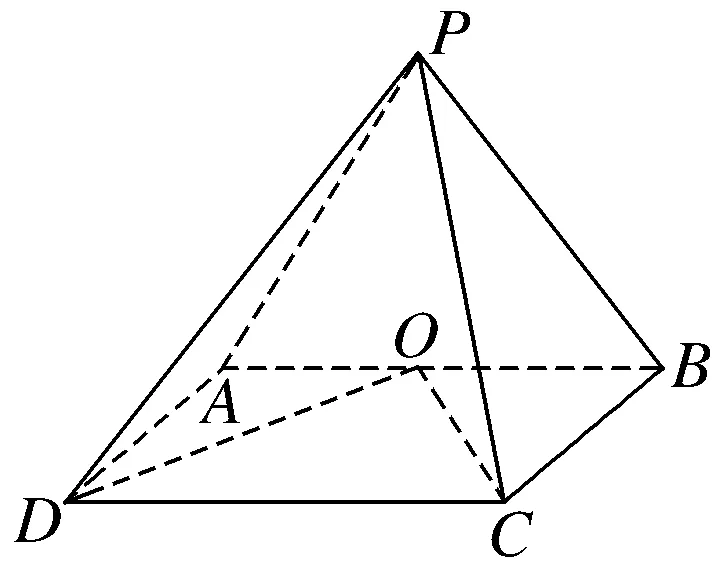
例题3 如图，在四棱锥P-ABCD中，侧面PAB⊥底面ABCD，底面ABCD为矩形，PA=PB，O为AB的中点，OD⊥PC.

(1)求证：OC⊥PD；

(2)若PD与平面PAB所成的角为30°，求二面角D-PC-B的余弦值．

解(1)证明：连接OP，∵PA=PB，O为AB的中点，∴OP⊥AB.∵侧面PAB⊥底面ABCD，

∴OP⊥平面ABCD，∴OP⊥OD，OP⊥OC.

∵OD⊥PC，OP∩PC=P，

∴OD⊥平面OPC，

∴OD⊥OC，又OP⊥OC，OP∩OD=O，

∴OC⊥平面OPD，∴OC⊥PD.

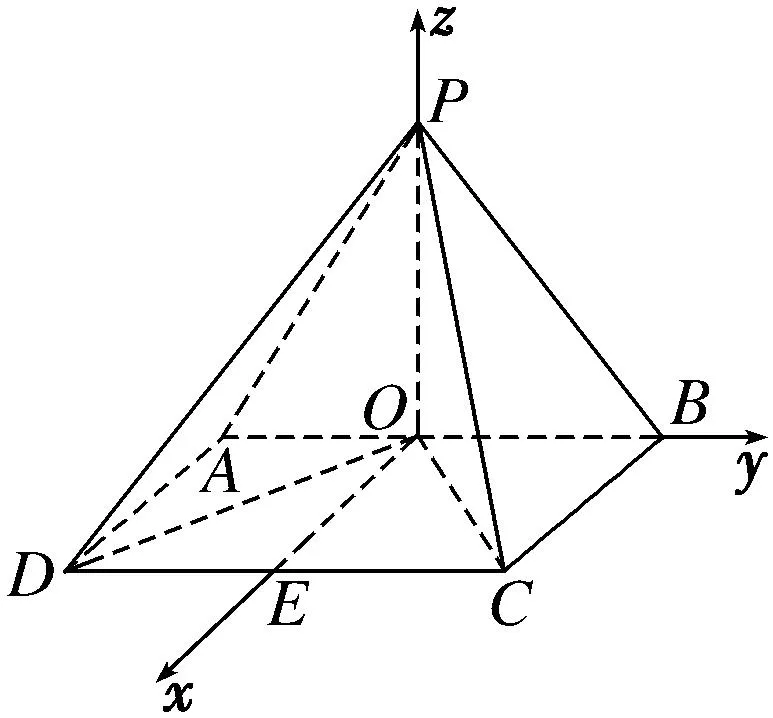
(2)取CD的中点E，以O为原点，OE，OB，OP所在的直线分别为x轴，y轴，z轴建立空间直角坐标系O-xyz.在矩形ABCD中，由(1)知OD⊥OC，∴AB=2AD，不妨设AD=1，则AB=2.

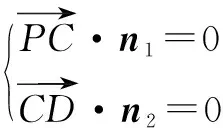
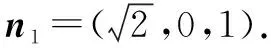
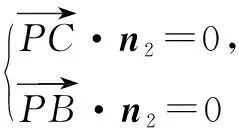
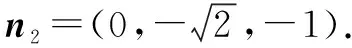
总之，立体几何解题的过程中常带有明显的规律性.只有不断总结,才能不断提高，专题复习课后要配套对应的练习，即讲即练，夯实到位，选取与课堂讲授内容相配套的题目，考查学生是否全面掌握.要强调立体几何解题书写的规范和要求，并参照评分标准强调解题格式的完整性.