三角函数的图象和性质高考考点题型归类解析

杜红全

(甘肃省康县教育局教研室 746500)

三角函数是高中数学的重要知识，也是高考重点考查的内容之一，而三角函数的图象和性质是高考的热点，题型既有选择题、填空题，又有解答题，多数是中低档题. 纵观近几年的高考题，发现其考点题型有以下几个方面，供参考.

一、最值或值域

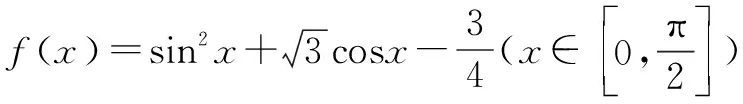
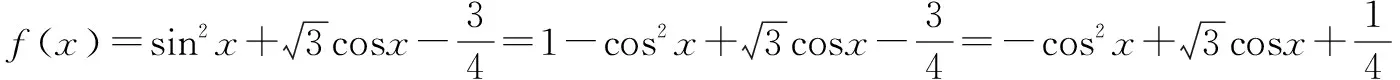
点评本题考查了三角函数的基本关系、二次函数在闭区间上的最值问题、三角函数的性质，考查了转化的数学思想、数形结合的数学思想.解本题的关键是把原解析式化为关于cosx的二次函数的形式，然后用配方法求解.有些题需把原解析式变形为y=Asin(ωx+φ)的形式后求最值或值域.多数情况下需要用配方法或三角函数的有界性来求最值或值域.

二、三角函数的奇偶性

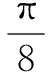
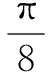
点评本题考查了三角函数图象的平移、三角函数的奇偶性.解答本题的关键是图象平移时函数解析式的变化以及根据奇偶性列出关于π的方程.

三、三角函数的周期性

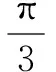
四、三角函数的单调性

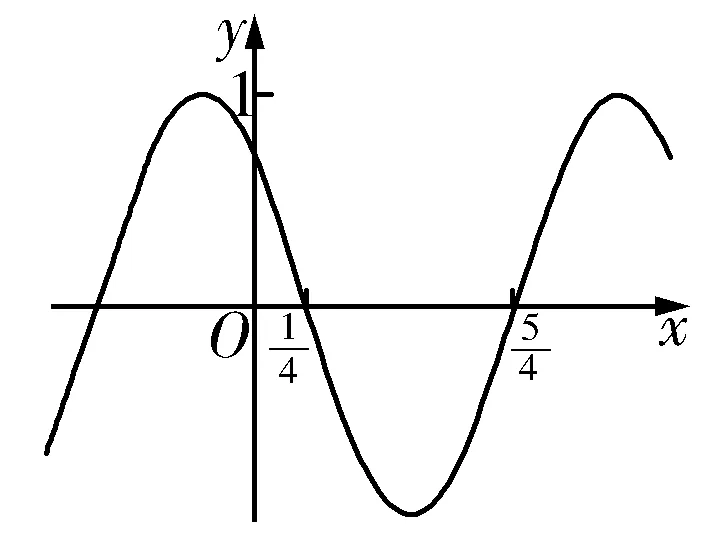
图1

例4 (2015全国，文8理8) 函数f(x)=cos(ωx+φ)的部分图象如图1所示，则f(x)的单调递减区间为

( )

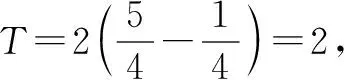
点评本题考查了三角函数的图象、三角函数的单调性. 解答本题的关键是根据函数的图象求出函数的最小正周期，难点是求φ的值，代入点求φ的值时，最好取三角函数图象的最低点或最高点.

五、三角函数的对称性

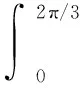
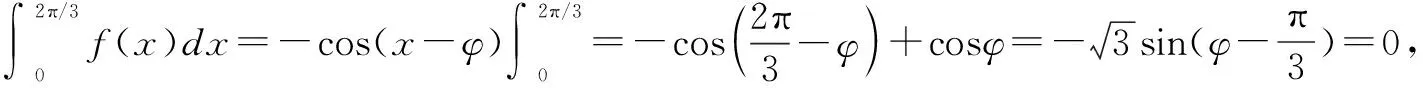
点评本题考查了定积分的几何意义、三角函数图象的对称性.解答本题的关键是利用定积分的几何意义及三角函数的图象，根据面积为0，得到x轴上方和下方的面积相等，从而找到三角函数的零点.若利用定积分的计算公式去求参数φ的值，运算量会相当大.

六、依图写式

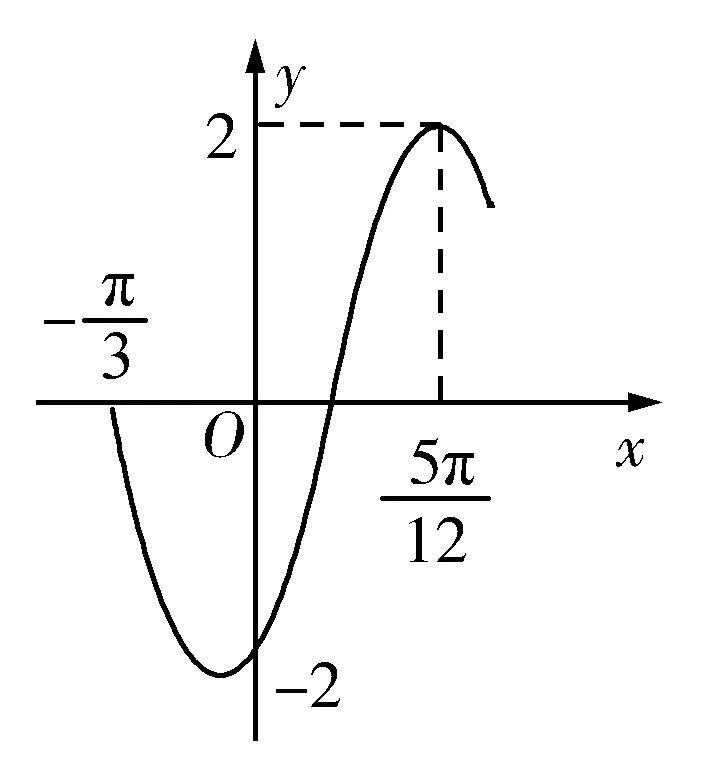
图2

( )

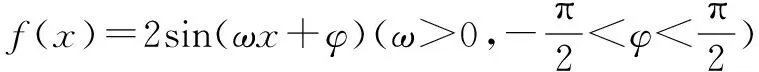
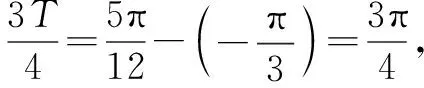
点评本题考查了三角函数的图象应用.已知三角函数的图象确定其解析式f(x)=Asin(ωx+φ)，常用方法就是待定系数法，先由图象中的最高点和最低点坐标确定A；再根据图象中所透露的函数的周期确定ω的值，最后根据图象中点的坐标求解φ的值.

七、依式选图

( )

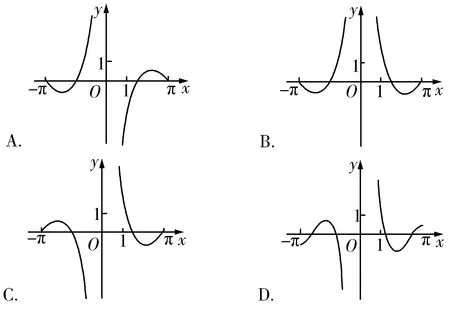
点评本题考查了三角函数图象性质.识别函数图象除利用函数的性质进行判断外，简单易行的办法就是用排除法，利用函数的定义域及图象上的坐标进行排除，特别是函数值的符号.

八、图象变换

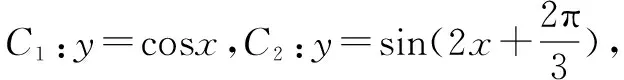
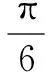
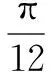
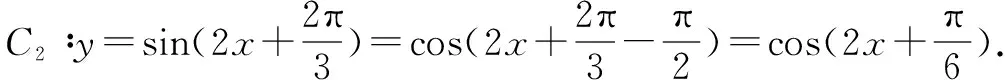
点评本题考查了三角函数图象变换.对于三角函数图象变换问题，首先要利用诱导公式将不同名函数转换成同名函数;在进行图象变换时，一般先平移后伸缩，而先伸缩后平移在考试中经常出现，无论哪种变换，都是针对自变量x而言.

九、综合应用

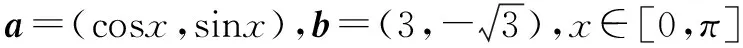
(1)若a∥b，求x的值；

(2)记f(x)=a·b，求f(x)的最大值和最小值以及对应的x的值．

分析(1)利用向量共线的坐标运算法则求解.(2) 利用数量积的坐标运算、辅助角公式，结合三角函数图象求解.

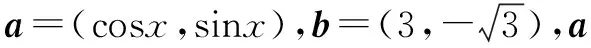
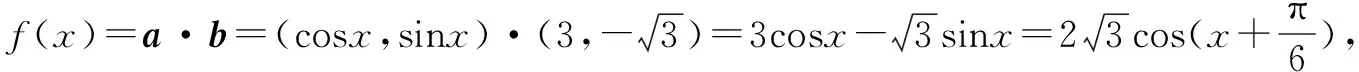
点评本题主要考查了平面向量共线的坐标表示、平面向量数量积的坐标运算、同角三角函数关系、两角和(差)的三角函数、三角函数图象与性质. 解答本题的关键是熟练应用：若a=(x1,y1),b=(x2,y2),则a∥b⟺x1y2-x2y1=0,a⊥b⟺x1x2+y1y2=0.