基于数学学科本质的解题思考——谈2015年高考福建理科卷三角函数试题的多维思考

杨苍洲

(福建省泉州第五中学 362000)

解题研究是高中数学的主要课题之一．但是大部分教师的解题研究常局限于题型、方法的归类，而忽视对学科本质的挖掘与应用．实则，理解数学的学科本质往往能引领你的解题走向成功．比如，可以考虑从数学的定义出发；可以考虑问题求解的通性通法；也可以考虑应用重要的数学思想方法．

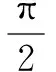
(1)求函数f(x)的解析式，并求其图象的对称轴方程；

(2)已知关于x的方程f(x)+g(x)=m在[0,2π)内有两个不同的解α,β．

①求实数m的取值范围；

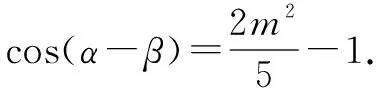
考完之后，笔者了解了部分考生，大部分考生在解答问题(2)②时感觉无从下手．如何准确地寻找解题入手点是解题的首要任务，笔者感觉可以从下面三个方面进行思考．

一、回归数学定义

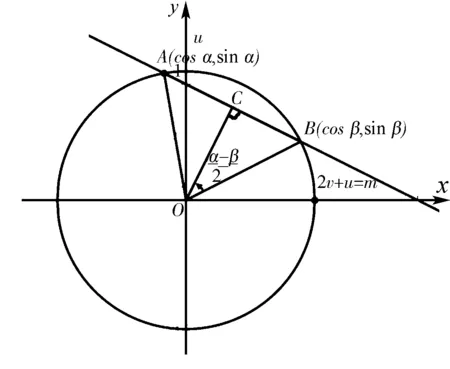
波利亚在其著作《怎样解题》中，认为“回到定义上去是一项重要的思维活动”．解题时，往往可以从定义出发．比如，本题可以考虑构造角度(α-β)，然后结合定义求解(α-β)的余弦值．

解法一回归三角函数定义

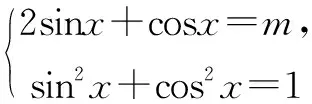
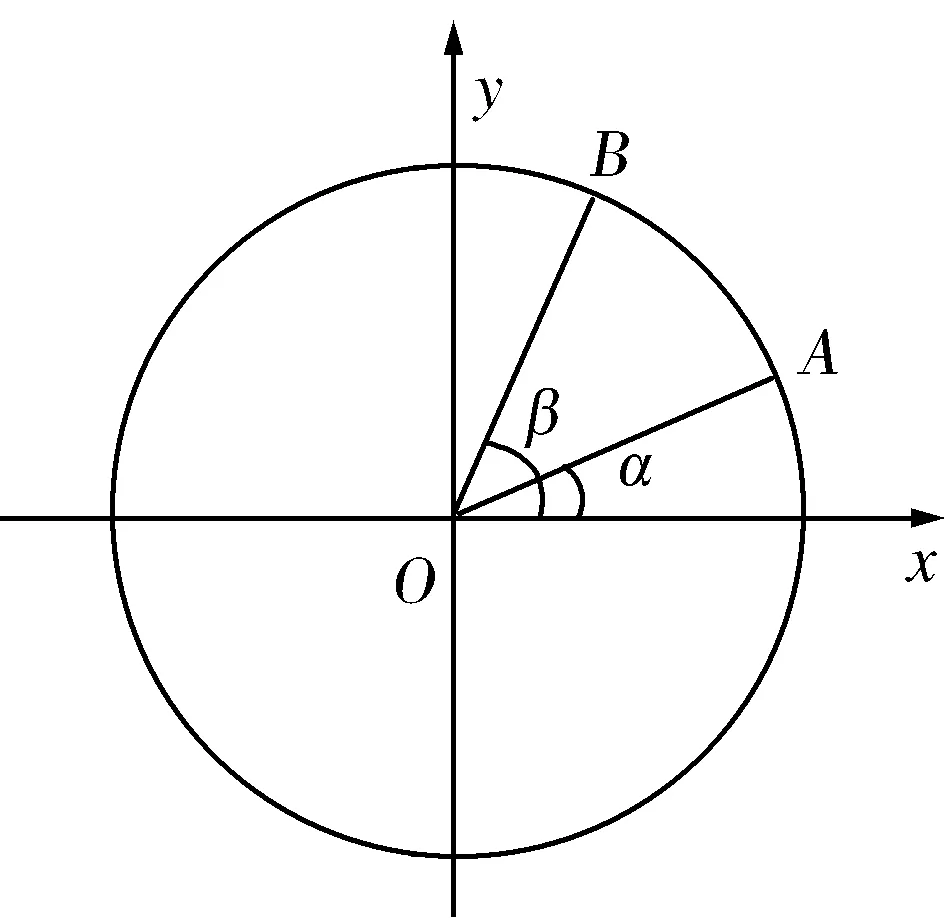
课本溯源本题的解法源自于普通高中课程标准试验教科书必修4-人教版P108，B组第2题：如图，在平面直角坐标系中，以原点为圆心，单位长度为半径的圆上有两点A(cosα,sinα)、B(cosβ,sinβ)，试用A、B两点的坐标表示∠AOB的余弦值．

二、应用通性通法

理解与掌握问题解决的通性通法对数学学习非常重要，是学习数学解题的根本．本题可以考虑从常规解题思路出发：利用辅助角公式化一角一函数，用同角三角函数的基本关系式进行正余弦值的转化，用角度的构造技巧得α-β=(α+φ)-(β+φ)，最后求出其余弦值．

解法二应用三角恒等变换

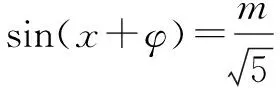
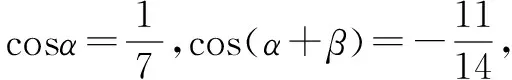
三、渗透数学思想

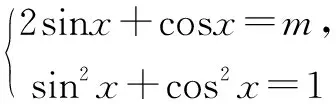
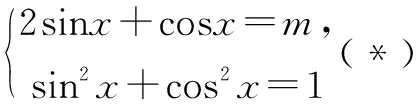
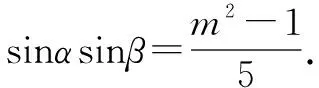
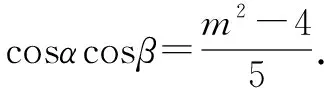
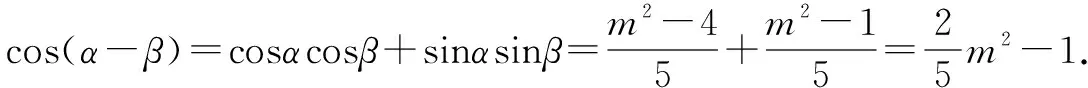
课本溯源本题的解法源自于普通高中课程标准试验教科书必修4-人教版P138，B组第2题：在三角形ABC中，已知tanA，tanB是x的方程x2+p(x+1)+1=0的两个实根，求∠C．