基于响应面理论的闸基底板脱空区域识别方法

黄锦林 ，李火坤，邓冰梅 ，4

（1.广东省水利水电科学研究院，广东 广州 510635；2.河口水利技术国家地方联合工程实验室，广东 广州 510635；3.南昌大学 建筑工程学院，江西 南昌 330031；4.南昌工学院，江西 南昌 330108）

1 研究背景

沿海省份的水闸，大部分都建于软土或砂土地基上，该类土体的变形、强度和稳定性问题十分突出［1］，闸基底部在上下游水位差下产生较大的扬压力，并且在长期的水流作用下易发生渗流，形成渗流通道，渗透水流极易带走底板下的细小颗粒，从而导致水闸底板容易发生脱空损伤。考虑到底板脱空位于水面以下，且为防止水闸上下游水位差过大而产生过大的扬压力，水闸一般不能完全抽干下游水，该现状导致水闸底板脱空的检查很难实施，所以该类损伤难以被发现，但脱空面积过大则容易引发安全问题，我国已发生多起因为水闸闸基隐患而导致水闸整体失事的惨剧［2］。

国内外专家、学者已开始有关水闸安全检测技术的研究工作，Carlsten等［3］利用雷达技术对大坝、水闸的基础侵蚀情况进行了探测；Maierhofer等［4］利用探地雷达和超声脉冲技术对两个运行超过一百年的老水闸进行了检测；McAllister等［5］基于随机裂纹增长理论，依托水闸的人字型闸门对焊接裂缝进行研究，根据裂缝的发展规律建立一种能预测裂缝发展的模型，有望应用在水闸结构裂缝预测当中；Estes等［6］对实测结果更新的可靠性进行了相关的分析研究，为实测数据处理奠定了基础；Alam等［7］、Zechner等［8］对水闸的渗漏问题进行了深度剖析，并对水闸渗漏机理进行研究，总结出水闸渗漏的规律。近年来我国也借助探地雷达和超声波技术进行有关水闸底板的脱空检测研究，戴呈祥等［9］、王世恩等［10］借助探地雷达对某实际水闸的底板进行探测，并在分析雷达图形特征的基础上对水闸的闸基隐患进行分类，实践表明该技术的应用前景较好，可以探测出脱空的位置和范围以及严重程度；安铎等［11］通过试验验证了探地雷达技术在水闸脱空检测上应用的可行性，可为判断闸基脱空提供一种新的检测方法；杨松华［12］将地质雷达用于马銮水闸的安全检测当中，分析1～6号探测剖面线，并和5处钻孔进行对比验证，表明该技术稳定，且能探测出底板脱空的范围和程度。陈鹦［13］应用动态检测方法，分别对5座水闸进行检测，并以动柔度和黏性阻尼系数作为判定依据对水闸底板的脱空进行分析，检测结果与实际情况吻合。

目前，水闸底板的检测技术主要有抽干水后的钻孔取芯、超声波法和探地雷达技术，其中钻孔取芯为有损检测，后期处理不好反而会加重水闸底板的结构损伤，对水闸的安全不利。超声波法和探地雷达为无损检测，有较好的前景，但同时也存在一些局限性，比如需在无水或水位极低的情况下进行检测，这种情况极不利于水闸的稳定，且影响水闸的正常运行。因此，本文应用响应面理论拟合出水闸的模态数据与底板的脱空参数间的关系，应用遗传算法对水闸底板脱空范围进行反演识别，有望为水闸的安全检测提供一种新的无损动态检测方法，提高水闸运行的安全性和可靠性。

2 脱空区域描述与分类

2.1 脱空区域描述为方便、直观和形象地展示软土地基上水闸的脱空状况，建立一个实体模型，以描述脱空区域，如图1所示。图1中灰色的上部结构为水闸结构，黑色的下部结构表示地基，地基空缺部分即表示脱空范围，如图1（b），脱空范围内地基无法给予水闸底板支撑而使整体受力情况发生改变，脱空范围越大，水闸受力越不均匀。

本文借助n个控制参数di（i=1，2，...，n）将水闸底板下的地基区域某一侧平均分成n-1段，控制参数的数值大小即为该侧向中间延伸的脱空范围，如图2所示。

图1 水闸底板地基脱空模拟示意

式中：x为图2中x坐标轴任意值；dx为x取任意值时的脱空参数；di为x取i时的脱空参数；L为x坐标轴方向水闸底板长度；n为脱空参数个数。

2.2 脱空区域分类根据脱空控制参数的个数、位置和方向等情况，对水闸底板的脱空区域进行分类，可分为单侧控制参数型脱空区域（如图3（a））和多侧控制参数型脱空区域，其中多侧控制参数型脱空区域又可分为相对侧控制参数型脱空区域（如图3（b））和贯穿型脱空区域（如图3（c））。图3中di是水闸底板的脱空控制参数值，阴影部分表示脱空的区域。

图2 水闸底板地基脱空参数描述

图3 脱空区域分类图

（1）单侧控制参数型脱空区域。该类型脱空区域可由脱空控制参数分布在一侧即可识别，如图3（a），为最简单的脱空类型。

（2）相对侧控制参数型脱空区域。该类型脱空区域需由脱空控制参数分布在相对侧才能识别，所涉及到的脱空控制参数相对较多，如图3（b），为较复杂的脱空类型，根据脱空所在位置能细分为上下游侧同时脱空和左右侧同时脱空。公路上混凝土面板脱空研究已经相对成熟，脱空测试技术和测试仪器相对先进。现有研究表明公路混凝土面板脱空规律为：首先在混凝土面板的4个角隅处出现脱空，随着时间的推移，角隅脱空的区域逐渐扩大，使横缝完全贯穿，之后扩展至纵向。水闸底板同样为混凝土面板，和公路混凝土面板有相似性，若脱空还未扩展至纵向时，则可用该类型脱空表示，可以推测该类型脱空存在的可能性较大。

（3）贯穿型脱空区域。该类型脱空区域需由脱空控制参数分布在相邻侧才能识别，所涉及到的脱空控制参数也相对较多，如图3（c），为较复杂的脱空类型，根据脱空所在位置和水流方向能细分为顺水流侧贯穿脱空和垂直水流方向贯穿脱空。水闸上下游水位差使得水闸受较大的扬压力作用，水流若经过闸底板发生闸下渗流，渗流作用可导致地基土中部分细小颗粒被带走，从而产生脱空，若未及时发现处理，地基土中被带走的颗粒逐渐增多，会使得脱空区域逐渐扩大，所以可以推测顺水流侧贯穿脱空存在的可能性很大。

3 基于响应面理论的闸基脱空识别方法

3.1 响应面理论响应面方法是数学方法和统计学方法相结合的产物，是公式结合一系列确定性试验拟合待定系数来体现函数的方法；借助拟合好的响应面模型代替复杂的有限元模型进行迭代计算，能明显提高计算效率，如今响应面理论发展较成熟且用途广泛。

响应面方程可以建立闸基底板脱空控制参数和结构模态参数间的显式关系，并作为实际结构的代理模型用于闸基底板脱空控制参数的反演。响应面方程建立过程如下。

（1）自变量筛选。以脱空控制参数作为基本输入变量，本文采用拉丁超立方抽样方法，确定输入变量样本集。

（2）因变量筛选。选取模态（各阶频率、振型）做为输出变量，针对各自变量样本点，在已经修正好的有限元模型中设置脱空范围内的EFS（弹性地基刚度）为零，模拟脱空以得到相应的结构模态参数，从而生成因变量集。

（3）响应面拟合。选择适当的响应面函数形式，根据自变量集及相应的因变量集，利用回归分析计算响应面方程中的系数，从而得到拟合好后的响应面模型。

常见响应面函数的形式有：径向基函数、非线性函数、多项式函数、BP神经网络和多元适应性回归样条函数等。

通过研究分析和试算，本文响应面模型选取三阶不带交叉项的响应面公式，形式如下：

其中，y为模态信息；xi为第i个脱空控制参数的脱空区域值，文中单侧脱空控制参数个数设为5，多侧脱空控制参数个数设为10；β为待定系数。

（4）响应面精度校验。在响应面模型拟合好以后，需对其精度进行校核，验证模型是否可靠。目前响应面模型的精度主要是通过以下几个评价指标来检验。

（1）复相关系数R2

式中：yRS为响应面模型计算结果；y为有限元模型计算的结果；N为设计空间上检验点数量；yˉ为有限元分析计算结果的平均值。

R2∈[0，1]，其值越接近于1，表示得到的回归响应模型就越接近于实际情况但并不表示响应面模型的精度就越高，回归方程中自变量个数的增加会导致R2的值变大。

式中：n为实验进行的次数；p为在所有输入及输出参数个数总和上加1。

修正的复相关系数是考虑p对实验的影响，当自变量个数增加时Radj2一定增加，故能一定程度上表示回归方程的拟合精度。

（3）相对均方误差RMSE

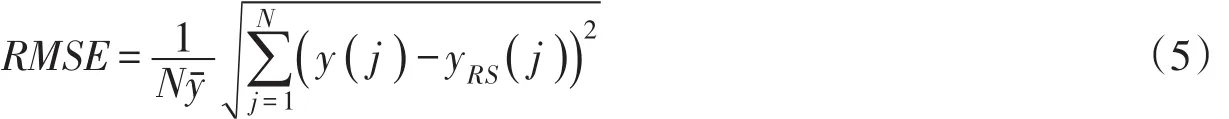
式中：yRS为响应面模型计算结果；y为有限元模型计算的结果；N为设计空间上检验点数量；yˉ为有限元分析计算结果的平均值。

RMSE越小则说明误差越小，拟合的精度就越高。

只有选取响应面精度较高的数据，才能保证后续反演的准确性。

3.2 响应面模型的拟合本文以某一实际水闸为例建立有限元数值模型，根据实测数据对有限元模型进行修正，该模型用于模拟大量不同的脱空工况（本文每类脱空工况取500组）以提取输出响应数据；考虑实际工程中动力检测数据获得的难易程度和可行性，本文在水闸底板脱空区域反演识别分析中选取水闸结构的频率和振型数据作为结构的输出变量。

对每一类型的脱空均选用三阶不带交叉项的响应面公式分别建立响应面模型，并用MATLAB编写拉丁超立方抽样程序进行抽样，对应不同脱空形式分别抽取500组脱空控制参数样本集。

在ANSYS有限元软件中，通过设置脱空控制参数值范围内的表面单元EFS置零来模拟实际水闸底板地基的脱空状态。结合水闸实体模型，提取出该类脱空形式的前n阶频率和测点振型值，应用响应面理论拟合出水闸的模态数据与底板脱空参数间的关系，即拟合出响应面公式中的待定系数，用拟合出的响应面模型替代有限元模型进行后续的脱空损伤识别。

结构模型测点位置的选取主要从3个方面进行考虑：（1）测点模态信息的灵敏度。测点信息的灵敏度越大，脱空越容易反应出来，测点信息越有效。（2）响应面精度。该精度关系到水闸底板脱空识别结果的准确性。（3）实际操作的可行性。水闸底板位于水面以下，测点位置一般选取在闸墩侧面的水面以上位置，特殊情况下可选取水面以下的测点。

本文综合这三个方面的因素选取测点的位置如图4，识别流程如图5所示。

图4 水闸实体模型和测点位置

图5 基于响应面的闸基脱空识别流程图

4 闸基底板脱空区域识别

基于遗传算法对闸基底板脱空的控制参数进行识别，遗传算法具有自适应能力、智能性和全局性等优点，能广泛用于求解较复杂的寻优问题以及多种非线性问题。

定义某实际工程（待识别的）的水闸结构固有频率向量为：

定义某实际工程（待识别的）的水闸结构振型值向量为：

定义本文中遗传算法的目标优化函数为：

式中：n为阶数；ω振型信息项的权值系数。

采用遗传算法对拟合好的响应面模型进行求解，通过局部搜索，可以寻找出一个满足目标函数的最优解，该最优解就是识别出的脱空控制参数的值，根据该值可以确定出脱空范围。

在实际水闸底板脱空检测中，由于有不可避免的误差存在，所以为了更贴合实际，本文也将进行有噪声情况下的水闸底板脱空识别，噪声的施加方法如下式所示：

式中：d为施加噪声前的模态值；dM为施加噪声后的模态值；γ为噪声水平；Ri是在［-1，1］之间的随机分别变量，利用公式进行误差的模拟，即加入噪声，根据施加噪声后的模态数据进行脱空控制参数的反演，从而能识别水闸底板的脱空区域。

为验证本文方法的可行性，从单侧型、相对侧型和贯穿型中分别选取一种假设的工况作为实际脱空工况进行计算验证，分别命名为工况一、工况二和工况三，脱空参数设置如表1所示。文中水闸底板实际脱空工况所对应的模态信息为有限元数值模型计算所得，在实际应用中则为工程的实测数据。

表1 水闸底板实际脱空工况 （单位：m）

单侧控制参数型脱空有5个控制参数，多侧控制参数型脱空有10个控制参数。工况一对应下游单侧脱空，d1、d2、d3、d4、d5为下游侧控制参数；工况二对应上下游侧同时脱空，d1、d2、d3、d4、d5为上游侧控制参数，d6、d7、d8、d9、d10为下游侧控制参数；工况三对应顺水流贯穿脱空，d1、d2、d3、d4、d5为中部靠左侧控制参数，d6、d7、d8、d9、d10为中部靠右控制参数。

将脱空对应的模态信息（工程的实测数据）输入至遗传算法中，可得最优解，即为识别出的脱空控制参数。文中目标优化函数取前三阶的模态信息，工况一至工况三在无噪声情况下的脱空控制参数识别结果如表2，识别结果和假设的实际脱空结果对比如图6所示。

表2 水闸底板脱空识别结果（无噪声） （单位：m）

图6 水闸底板脱空识别结果（无噪声）

在无噪声的情况下，本文方法能识别出该三种工况的水闸底板的脱空区域，吻合度较高，说明理论上本文方法用于水闸底板脱空区域的识别是可行的。

为了更贴合实际，本文将进行有噪声情况下的水闸底板脱空识别。施加噪声级别为3%的高斯白噪声来模拟实际操作中不可避免的误差。工况一至工况三在3%噪声情况下的脱空控制参数识别结果如表3和图7所示，其中，反演识别时，工况一中目标优化函数取前三阶模态信息，工况二和工况三目标优化函数取前六阶模态信息。

表3 水闸底板脱空识别结果（3%噪声） （单位：m）

图7 水闸底板脱空识别结果（3%噪声）

目标优化函数中信息量不同的情况下，三种工况的识别结果精度相当，原因可能是工况二、工况三的控制参数增加至10个，使得反演识别难度加大；结果显示三种工况在3%噪声情况下均能大致识别出脱空位置和形状，识别结果对定性判断是否脱空和脱空的形状有指导作用，相比于无噪声情况下识别精度有所下降，但总的来说本文方法对水闸底板脱空识别是可行的，且该模型和算法有一定的抗噪能力。

5 结论

本文针对水闸底板脱空问题，先对脱空区域进行参数化描述与分类，根据混凝土板的脱空规律和水闸底板所处的特殊环境重点对三种类型的脱空进行模拟验证；对不同的脱空类型分别建立脱空控制参数与结构模态之间的响应面模型，并借助拟合好的响应面模型取代有限元模型进行计算分析；对水闸底板最可能出现的三种脱空工况进行试算和识别。结果表明：本文提出的方法在无噪声情况下能准确识别出水闸底板脱空的区域和形状，吻合度很高；在噪声级别为3%情况下能大致指示出脱空的区域，有一定的抗噪能力。后期可以通过研究算法的抗噪能力和测点优化布置等来提高识别精度，有望为水闸安全检测增加一种新的无损检测方法。