网络设备销售收入的预测与应用

刘墨德

（1.三明学院 信息工程学院，福建 三明 365004；2.工业大数据分析及应用福建省高校重点实验室，福建 三明 365004；3.数字福建工业能源大数据研究所，福建 三明 365004）

科学预测网络设备销售收入对该公司的发展十分重要，因为错误的预测会让公司浪费宝贵的人力、物力、财力，甚至断送公司。

由于大数据时代各种资料的积累受到广泛的重视，计算机网络技术迅速发展，运用日趋完善，人类有效进行预测活动的方法及手段已经具备，因此科学预测该公司未来网络设备销售收入可以实现。

要进行正确的预测是有难度的，主要体现在以下几个方面：

（1）随着科学技术的发展，各种因素、现象之间的联系越来越复杂，正确预测未来的难度越来越大。

（2）人类认识能力是有限的，预测要求人类能超越现实，理解未来，但人类的理解力又局限于自身的经历，这是一个难以解决的矛盾，因此人类并不能得出准确的预测结论。

（3）虽然人类可以采用概率统计的方法来研究并揭示非确定性事件的概率，但人类无法消除这些事件的非确定性，预测的难度来源于未来所具有的非确定性。

（4）预测过程本身存在“干扰”未来的现象：当人们预感前景不妙时，便会设法阻止其出现，这是“自毁”性预测；当前景不错时，人们会努力促使它尽快实现，这是“自成”性预测。

某网络设备公司2006-2015年的网络设备销售收入如下表所示，时间序列数据呈现抛物线形状，试预测2016年的销售收入为多少万元？网络设备销售收入数据见表1。

表1 网络设备销售收入数据表

针对上述预测难度，为了正确预测该公司的网络设备销售收入，建立最小二乘法和三点法两种不同模型进行预测与应用分析。

1 二次曲线趋势外推预测法的提出

二次曲线趋势外推预测法是研究时间序列观察值数据随时间变化呈现一种由高到低再到高或由低到高在到低的趋势变化的曲线外推预测法，由于时间序列观察值的散点图呈现抛物线形状，所以也称二次曲线趋势外推预测法。

设xt为时间变量（自变量）为第t期时间变量xt的预测值（因变量），yt为第t期时间变量xt的观察值，则为二次曲线趋势外推预测法的数学模型，其中a,b,c为待定常数为第 t期离差为离差平方和。

二次曲线趋势外推预测法适用于时间序列数据呈现抛物线形状上升或下降，且曲线仅有一个极值（极大值或极小值）的情况下使用，可通过使误差为最小的标准来确定待定常数a,b,c，求出数学模型进行预测分析。

2 用最小二乘法预测与应用分析

2.1 待定常数的算法分析

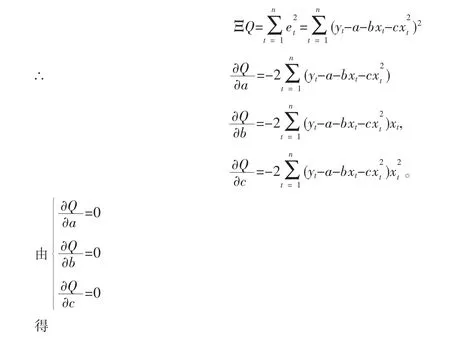
这里要注意到，自变量xt的取值为1到n，也就是说自变量xt取值等于其下标t，即xt=t。而实际上，从抛物线趋势法的原理来讲，时间变量xt的取值代表的是时间变量的编号，而这种编号不一定要从1开始，可以从任一自然数开始顺序编号，因此可以利用这样的便利减少计算工作量。当时间序列的数据长度n为奇数时，取中位数（n+1）/2的编号为0，那么xt就构成了以0号为中心的正、负数对称的顺序编号，即于是

所以（1）可简化为

由（2）解得

2.2 预测步骤

（1）根据所给实际问题的观察值绘制散点图。

（2）根据散点图的变化趋势确定实际问题属于二次曲线变化趋势后，列表计算二次曲线待定常数所需数据。

（3）确定待定常数，建立预测模型。

（4）计算预测值。

2.3 算例（见案例）

解：（1）绘制时间序列数据散点图（图略），由散点图可知，销售收入变化趋势属于二次曲线变化趋势，选择二次曲线预测模型。

（2）列表计算最小二乘法所需数据:

年份2007 2008 2009 2010 2011 2012 2013 2014 2015∑xt-4-3-2-1 0 1 2 3 4 0 yt 545 641 764 923 1107 1322 1568 1836 2140 10846 xt 2 16 9 4 1 0 1 4 9 1 6 60 xt 4 256 81 16 1 0 1 1 6 81 256 708 xtyt-2180-1923-1528-923 0 1322 3136 5508 8560 11972 xt 2yt 8720 5769 3056 923 0 1322 6272 16524 34240 76826 y^t 543.89 640.73 766.91 922.43 1107.29 1321.49 1565.03 1837.91 2140.13（yt-y^t）2 1.23 0.07 8.47 0.32 0.08 0.26 8.82 3.65 0.02 22.92

（3）确定待定常数，建立预测模型。

利用上表计算得

（4）计算预测值。

将xt=5代入中，得2016年的销售收入预测值为

3 用三点法预测与应用分析

3.1 三点法确定待定常数的思路分析

用三点法确定待定常数的思路是：在二次曲线模型上选取远、中、近期三点坐标作为预测模型待定常数a，b，c的估计值。其具体做法是，使时间序列的总项数n为奇数（若n为偶数，可删去最初的一个观察期数据）；如果n≥15，则在时间序列的远、中、近三期各取5个数据项，用权数w=1,2,3,4,5由远到近分别赋权并进行加权平均；如果15≥n≥9，则在时间序列的远、中、近三期各取3个数据项，用权数w=1,2,3由远到近分别赋权并进行加权平均。并以此三个加权平均值作为该二次曲线预测模型上远、中、近三点的纵坐标的数值，对远、中、近三点的横坐标也作权数相同加权平均值作为该二次曲线预测模型上远、中、近三点的横坐标的数值，然后联立方程组求出待定常数 a，b，c。

3.2 取5项观察值确定待定常数的算法分析

假设远、中、近期三点坐标分别为 P1（t1，R），P2（t2，S）,P3（t3，T）因为时间序列的总项数 n 为奇数，所以中间项为当 n≥15时， 取远期 5个观察值 y1，y2，y3，y4，y5， 其加权平均值为 R=取中期5个观察值yd-2，yd-1，yd，yd+1，yd+2，其加权平均值为S=取近期5个观察值yn-4，yn-3，yn-2，yn-1，yn，其加权平均值为T=对远、中、近三点的横坐标 t1，t2，t3，作权数 w=1,2,3,4,5加权平均值得 t1=于是5项观察值作加权平均后三点坐标分别为P1将点 P1，P2，P3代入二次曲线预测模型中，得联立方程组

3.3 取3项观察值确定待定常数的算法分析

当15≥n≥9时，取远期3个观察值y1,y2,y3，其加权平均值为取中期3个观察值yd-1，yd，yd+1， 其加权平均值为取近期3个观察值yn-2，yn-1，yn，其加权平均值为S=对远、中、近三点的横坐标 t1，t2，t3，作权数 w=1,2,3 加权平均值得于是3项观察值作加权平均后三点坐标分别为将点 P1，P2，P3代入二次曲线预测模型中，得联立方程组

3.4 用三点法预测分析的特点[3]

(1)三点法不需要观察值的全部数据，计算比较简单。

(2)对选取的数据比较敏感，即便是取加权平均值，预测结果也会因为选取数据方式不同而受到一定的影响。

(3)一般而言，每一组里的数据相对较多时，预测模型会越接近于实际。

(4)每一组里的数据个数要求是奇数，是为了方便计算。

(5)三点法的计算比最小二乘法方便，但因采集数据较少，所以用三点法作预测所产生的误差比用最小二乘法作预测所产生的误差大。

3.5 算例（见案例）

解：(1）绘制时间序列数据散点图（图略），由散点图可知，销售收入变化趋势属于二次曲线变化趋势，选择二次曲线预测模型。

(2）列表计算三点法所需数据:

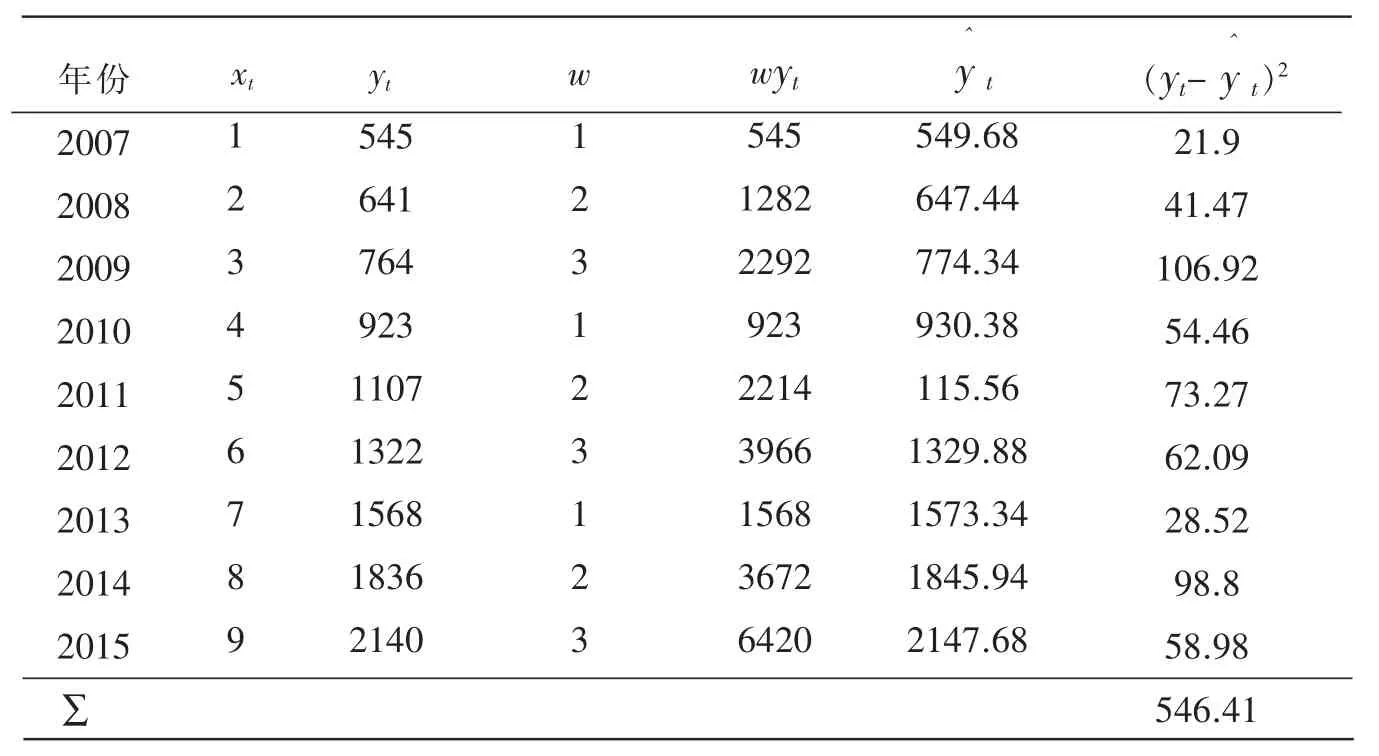
年份2007 2008 2009 2010 2011 2012 2013 2014 2015∑xt 1 2 3 4 5 6 7 8 9 yt 545 641 764 923 1107 1322 1568 1836 2140 w 1 2 3 1 2 3 1 2 3 wyt 545 1282 2292 923 2214 3966 1568 3672 6420 y^t 549.68 647.44 774.34 930.38 115.56 1329.88 1573.34 1845.94 2147.68（yt-y^t）2 21.9 41.47 106.92 54.46 73.27 62.09 28.52 98.8 58.98 546.41

(3）确定待定常数，建立预测模型[4]。

(4）计算预测值。

将xt=10代入：中，得2016年的销售收入预测值为

5 讨论

算例3.5与算例2.3均为预测2016年的销售收入，均是对时间序列数据呈现抛物线形状的同一实际问题进行有效预测，只是使用的方法不同,算例2.3的运算复杂性比算例3.5大，算例2.3的最小二乘法更适用于大中型精密的预测，算例3.5的三点法更适用于小型简便快捷的预测。由于算例3.5的样本均方差大于算例2.3的样本均方差，所以算例2.3的预测值比算例3.5的预测值准确、可靠。两个预测值的相对误差限为是一个较小数据，所以两个预测值均可接受。