金红石TiO2中本征缺陷扩散性质的第一性原理计算∗

刘汝霖 方粮 郝跃 池雅庆

1)(国防科技大学,高性能计算国家重点实验室,长沙 410073)2)(国防科技大学计算机学院,长沙 410073)3)(西安电子科技大学微电子学院,宽禁带半导体材料与器件教育部重点实验室,西安 710071)(2018年4月26日收到;2018年5月26日收到修改稿)

1 引 言

二氧化钛作为一种常见的半导体材料,在高-k介质[1]、阻变器件[2−6]、自旋电子器件等新型存储器件研究领域备受关注.研究发现,各类缺陷的存在对材料的电子结构[7,8]、磁学[9]等性质产生重要影响.在不同的缺陷类型中,本征点缺陷源于热涨落过程中晶格振动,是一类普遍存在的缺陷类型.理论上,二氧化钛晶体中存在6种本征点缺陷,采用Kröger Vink缺陷符号可以表示为:钛间隙TiI、钛空位VTi、氧间隙OI、氧空位VO、钛的反位缺陷TiO、氧的反位缺陷OTi.由于钛离子和氧离子的电性差异及离子半径差异,反位缺陷形成的难度较大[10],本文仅对其他4种缺陷进行研究,其生成的反应方程如下[11]:

反应方程中,OO和TiTi分别表示格点氧原子和钛原子,VI表示空的晶格间隙,e和h分别表示电子和空穴.符号上标中的“•”和“′”分别表示相对带电量为+1和−1,下标表示当前粒子出现的位置.自然形成的二氧化钛晶体表现还原性,如(1)或(2)式所示,分别表示晶格格点出现VO以及晶格间隙出现TiI.相应地,根据晶格中原子数目的化学计量比和缺陷类型,文献中常将此还原态的二氧化钛表示为TiO2−x或Ti1+yO2(x,y均为正数).

沿x方向一维缺陷的扩散流密度[11]如(5)式所示,式中Ji表示扩散流密度,a为扩散平均距离,vi为晶格振动频率,Ea为缺陷扩散激活能,k为玻尔兹曼常数,T为温度,ci为缺陷密度,表示缺陷浓度梯度.在当前TiO2扩散性质的研究中,对主导缺陷粒子的种类和扩散方式还存在较大分歧.其中,单就激活能大小及扩散路径这一问题而言,尚未形成一致性结论.Hunting和Sullivan[12]根据实验数据认为TiI为主导缺陷,且间隙空间较大的[001]方向比[100]方向(与[010]方向等价)具有更小的迁移势垒,缺陷扩散表现出各向异性.Iddir等[13]采用密度泛函理论方法计算了两类缺陷的在晶格中的扩散势垒,结果发现TiI沿[100]方向的替位扩散(又称interstitialcy或kick-out方式)具有最低的能量势垒.

针对缺陷研究中的争议问题,本文选取二氧化钛同质异构体相中最稳定的金红石相(rutile)为例,对钛间隙TiI、钛空位VTi、氧间隙OI、氧空位VO4种本征缺陷的扩散过程进行建模,采用CI-NEB方法计算扩散势垒,并针对计算结果对扩散路径进行了讨论.

2 计算方法

计算基于密度泛函理论(density functional theory,DFT)的QE(quantum-ESPRESSO)软件包[14,15],交换关联能的处理采用广义梯度近似(generalized gradient approximation,GGA)中的Perdew-Burke-Ernzerhof for solid(PBEsol)泛函[16],赝势文件由Standard Solid State Pseudopotentials(SSSP)提供[17,18].所有参与计算的结构均基于3×3×4超晶胞(含216个原子),通过增加或移除相应单一原子并进行结构弛豫而来.计算中波函数截断能设定为650 eV,布里渊区k点网格设置为gamma点.晶格弛豫几何收敛阈值为原子间作用力3.0×10−2eV/Å,内应力5.0×10−2GPa,自洽循环迭代收敛阈值为1.0×10−6eV/atom.过渡态搜索采用CI-NEB方法[19],误差阈值设定为0.05 eV/Å.

文中使用的原子结构图由VESTA[20]软件绘制,NEB过渡态势垒图曲线由Python Matplotlib绘图库采用双线性插值方式绘制,电荷布局分析采用Bader分析方法[21−24].

3 计算结果与讨论

3.1 本征缺陷建模

如表1所列,采用SSSP赝势对金红石3×3×4超晶胞进行几何优化并折算为单胞的晶格常数数值,实验值与计算值的差异均远小于1%,计算结果与实验数据高度一致.

表1 几何弛豫优化后的晶胞参数与实验值的对比Table 1.Comparison of structural parameters calculated by DFT with experimental result.

在金红石中,半径较大的氧离子密堆积排列构成晶格主体,其中一半的间隙位置被半径较小的钛离子以填隙方式占据,形成稍微形变的TiO6八面体基本单元[26],如图1所示.原子结构图中原子相对大小采用实际离子半径表示[27],其中较大的红色球体表示正常晶格格点的氧原子OO;天蓝色球体表示正常晶格格点的钛原子TiTi.在单个TiO6八面体单元中形成了6条Ti–O键,其中4条较短为1.941 Å,两条稍长为1.976 Å,习惯将4条较短键所在平面成为赤道面,面上结构在[100]和[010]两个方向等价.不同的八面体单元通过共用赤道面的两条棱边连接成链,不同链间则通过共顶点的方式形成三维结构的稳定晶体.共棱棱长为2.531 Å,非共棱棱长为2.943 Å,在本文中也称为赤道面短边和长边.

图1 金红石TiO2的原子结构示意图,其基本构成单元为TiO6八面体结构Fig.1.Schematic diagram of atomic structure of rutile TiO2with basic unit of TiO6octahedral symmetry.

为了便于对结构进行描述,本文采用原子结构示意图描述缺陷,并辅以相对晶格常数坐标定位.通过在未被占据的八面体中心引入单个钛间隙TiI、氧间隙OI,或在晶格格点位置引入钛空位VTi、氧空位VO,并进行晶格弛豫计算获得稳定结构并作为扩散初态.同理,通过对初态中缺陷进行平移可获得扩散末态.鉴于超晶胞中同种原子是等价的,初、末态中单个缺陷的位置可以任意选取,仅需保持平移向量不变即可.模型中等效缺陷比例为0.5%,由于金红石介电常数较大,缺陷间相互作用可以忽略.

Bader电荷分析表明,完美晶格中O离子名义电荷为−1.1,Ti离子名义电荷为+2.2,TiI缺陷名义电荷为+1.9,OI缺陷名义电荷为−0.6.由此可见,缺陷的引入会对于离子电荷分布造成较大影响,如果体系存在外场作用时应当引起注意.

3.2 扩散路径与势垒分析

3.2.1 TiI钛间隙扩散

在未占据的TiO6中心引入Ti原子并进行原子弛豫计算,结果显示TiI与周围的O离子形成了新的TiO6八面体结构.该TiI钛间隙不等价的扩散路径有3种可能:沿[001]方向(平行c轴方向)的填隙扩散;沿[110]方向(垂直于c轴方向)的填隙扩散;沿[100]方向(与[010]方向等价,垂直于c轴方向)的替位扩散.

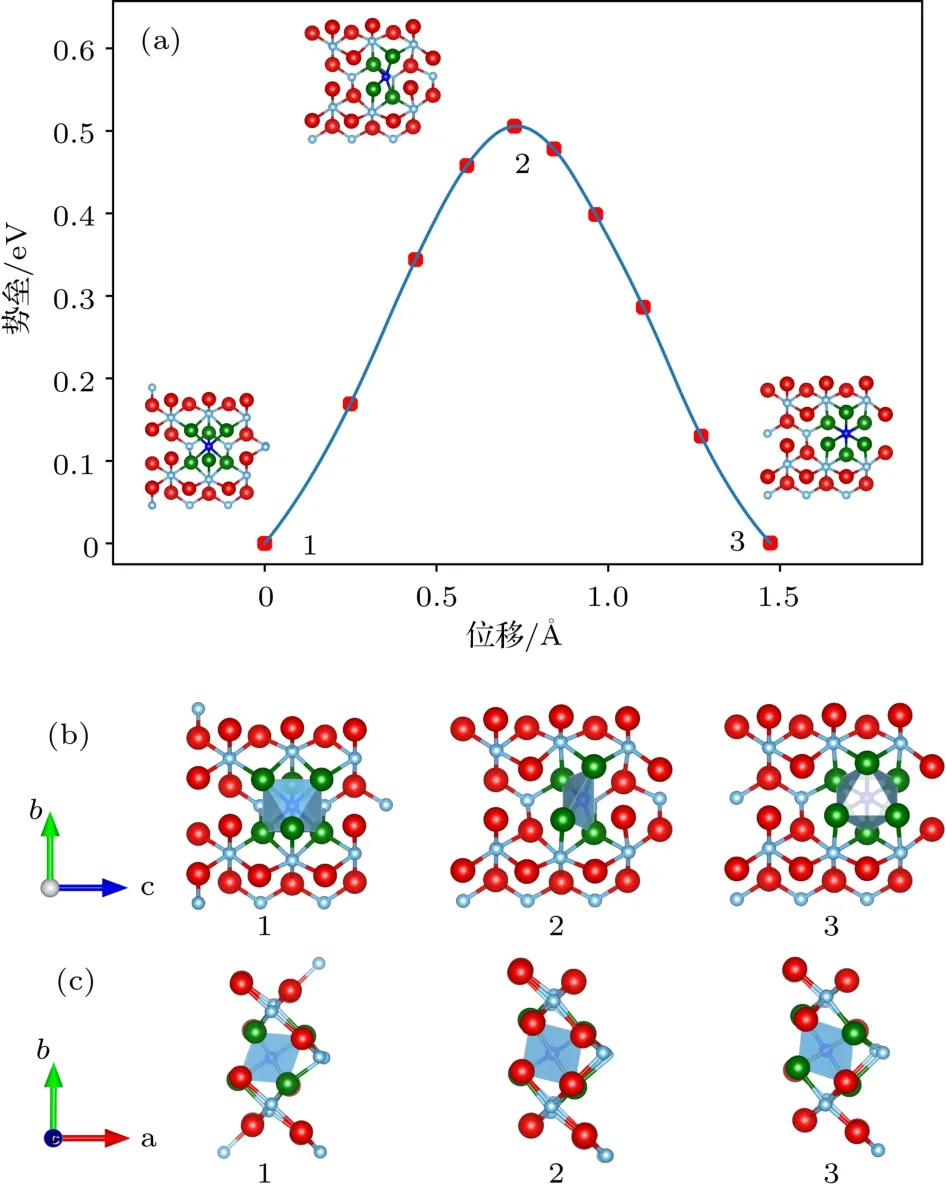
图2 TiI沿[001]方向的填隙扩散过程示意图,图中蓝色标注为TiI,绿色标注为临近格点上的O原子 (a)扩散势垒示意图;(b),(c)分别为沿[100]和[001]方向投影的多面体视图Fig.2.Schematic diagram of interstitial diffusion of TiIalong[001],of which TiIis colored blue and the adjacent O atoms are colored green:(a)Diffusion barrier.(b),(c)polyhedral view of[100]and[001]direction,respectively.

图2为TiI沿[001]方向的填隙扩散示意图,图中原子结构截取自3×3×4超晶胞.如图2(a)所示,路径中3个像点TiI缺陷的坐标可近似表示为(0,0,0),(0,0,0.25c),(0,0,0.5c),初、末态等价结构之间的位移为1.46 Å,扩散激活能为Ea=0.5057 eV,该值与扩散实验值0.4–0.68 eV一致[28,29].从图2(b),图2(c)的多面体结构图可以看出,TiI初、末稳态均为TiO6的八面体结构,而势垒最高点位置则为TiO3四面体结构.

图3为TiI沿[100]方向的替位扩散示意图,图中原子结构截取自3×3×4超晶胞.如图3(a)所示,TiI的替位扩散过程是通过间隙原子取代晶格格点原子,后者进入下一个间隙位置.体系能量变化呈现为“M”形,其激活能为Ea=1.0024 eV(图中像点1,2结构的能量差),最终等效于TiI沿[100]方向位移4.57 Å,约为晶格常数a.结合图3(b)的原子结构图可以看出,TiI在扩散过程中会形成2TiI+VTi的过渡结构(图中像点3位置),其激活能为Ea=0.2208 eV.

图3 TiI沿[100]方向的替位扩散过程示意图 (a)扩散势垒示意图;(b)沿[001]方向投影原子视图,蓝色表示参与扩散过程的Ti原子Fig.3.Schematic diagram of interstitialcy diffusion of TiIalong[100]:(a)Diffusion barrier;(b)atomic view of[001]direction,blue represents the Ti atom that participates in the diffusion process.

图4为TiI沿[110]方向的填隙扩散示意图.如图4(a)所示,路径中标注的3个像点TiI缺陷的坐标可近似表示为(0,0,0),(0.3a,0.18a,0),(0.5a,0.5a,0),初、末态等价结构之间的位移为扩散激活能为Ea=2.7758 eV.相比于TiI间隙的前两种扩散路径,沿[110]方向扩散所需激活能较大,这是由于扩散过程晶格局部原子排布发生了较大改变.如图4(a)中像点2所示,路径中的Ti格点原子发生位移并形成2TiI+VTi的过渡结构(像点2).结合图4(b)的多面体结构示意图,在像点2过渡结构的稳定状态中,所有Ti原子都形成了TiO6八面体构型,这与[100]方向扩散过程类似.

图4 TiI沿[110]方向的填隙扩散过程示意图,蓝色表示参与扩散过程的Ti原子 (a)扩散势垒示意图;(b)沿[001]方向的多面体原子视图Fig.4.Schematic diagram of interstitial diffusion of TiIalong[110],blue represents the Ti atom that participates in the diffusion process:(a)Diffusion barrier;(b)atomic view of polyhedron along[001]direction.

3.2.2 OI氧间隙扩散

由于离子半径较大,OI无法进入到间隙中,如图5(b)和图5(c)原子结构图中初、末态(像点1,3)所示,晶格弛豫后OI的稳态位置靠近周围正常的O格点.综合各子图,OI沿[001]方向的扩散过程中,实际上是沿着共棱TiO6链在顶点与赤道面之间运动,扩散激活能Ea=0.859 eV.

与TiI的替位扩散类似,OI也存在替位扩散,图6为OI沿[110]方向的替位扩散过程,激活能Ea=0.902 eV.对比发现,OI沿[110]方向替位扩散激活能高于沿[001]方向的扩散,与TiI的替位扩散势垒接近.

图5 OI沿[001]方向扩散过程示意图 (a)扩散势垒示意图;(b),(c)沿[001]和[100]方向投影的原子结构视图,图中绿色原子标识为OIFig.5.Schematic diagram of diffusion process of OI along[001]:(a)Diffusion barrier;(b),(c)atomic structure view projected along[001]and[100]direction,in which OIis colored green.

图6 OI沿[110]方向进行替位扩散示意图 (a)扩散势垒示意图;(b)沿[001]方向投影的原子结构视图,图中绿色原子标识为OIFig.6.Schematic diagram of interstitialcy diffusion of OIalong[110]:(a)Diffusion barrier;(b)atomic structure view projected along[001]direction,in which OI is colored green.

图7 VO空位扩散示意图 (a)扩散路径的原子结构示意图,数字表示不同的扩散路径;(b)–(d)图(a)中路径1,2,3的扩散势垒Fig.7.Schematic diagram of diffusion pro file of VO:(a)Schematic diagram of atomic structure of diffusion paths,numbers represent different diffusion paths;(b)–(d)diffusion barrier of path 1 to 3 in fig.(a).

图8 VTi空位扩散示意图 (a)扩散路径的原子结构示意图,其中白色原子表示VTi,蓝色原子表示扩散路径上晶格格点Ti原子,数字标记1和2表示扩散的两种可能路径;(b)–(c)路径1和路径2的跃迁势垒示意图Fig.8.Schematic diagram of diffusion pro file of VTi:(a)Schematic diagram of atomic structure of VTidiffusion path,the white and blue ball represent VTiand Ti on diffusion path,respectively,digital markers 1 and 2 represent the two possible paths for diffusion;(b)–(c)diagram of transition energy barrier of path 1 and 2,respectively.

3.2.3 VO氧空位扩散

图7为VO的3种不等价扩散路径示意图,其中路径1表示沿[001]方向的八面体非共棱侧格点间扩散,激活能为E1a=1.747 eV;路径2表示沿[110]方向的八面体共棱侧格点间的扩散,激活能为E2a=0.735 eV;路径3表示八面体顶点与赤道面格点间的扩散,激活能为E3a=1.119 eV.Nowotny等[30]通过实验测定激活能为1.38 eV,远高于路径2的势垒,通过对扩散路径的进一步分析可知,VO长程扩散至少需要以上两种路径配合,因此VO扩散路径的激活能不小于Ea=1.119 eV,计算结果与实验数据相符.

3.2.4 VTi钛空位扩散

图8为VTi的两种扩散路径示意图,路径1表示沿[111]方向的相邻共顶点的两个八面体中心交换VTi空位和格点Ti原子,激活能为E1a=2.375 eV;路径2表示沿[001]方向在相邻共棱的两个八面体中心交换VTi空位和格点Ti原子,激活能为E2a=3.232 eV.结合图1的原子结构图,由于TiO6八面体共棱的O原子间隙相对更小,这也导致了Ti原子横穿过程需要克服相对较高的势垒.Nowotny等[30]通过实验改变氧分压浓度,当超过某一临界值后,金红石晶体的导电特性会发生n型到p型的转变,此时晶体中浓度最高的缺陷种类为VTi,激活能约为2.57 eV,结果与计算值符合.

4 结 论

基于DFT研究了金红石相TiO2中4种本征缺陷的扩散行为,采用CI-NEB方法对不同缺陷类型的扩散过渡态进行了研究,主要结论如下.

1)缺陷TiI由于离子半径较小,倾向于填充可以形成八面体TiO6结构的位置,四面体位置填充并不稳定;而OI由于离子半径相对较大,倾向于拥挤在OO晶格格点位置附近.

2)由于晶格结构的各向异性,缺陷的扩散路径和过渡态势垒高度也存在显著的各向异性.通过对比扩散势垒大小并作为判断扩散行为的主要依据,钛间隙TiI沿[001]方向的填隙扩散过程在所有缺陷扩散类型中所需的激活能最小.另外,在扩散路径的选择上,氧间隙OI也倾向于沿[001]方向进行扩散,这是因为虽然氧空位VO在沿[110]方向共棱的八面体短边扩散势垒小于其他方向,但其长程扩散至少包含两种扩散路径的组合,所以扩散势垒高于氧间隙.钛空位VTi则倾向于在沿[111]方向的共顶点的八面体之间交换Ti原子.

3)通过对TiI和OI沿[001]方向扩散势垒比较发现,较小的离子半径在[001]方向具有更小的扩散势垒高度,因此推测,跃迁势垒与离子半径大小有关.该项结论还需更多计算结果加以证明.

感谢国防科学技术大学高性能计算国家重点实验室提供计算支持.