高温等离子体中太赫兹波的传输特性
孟令辉 任洪波 刘建晓
(衡水学院物理与电子信息系,衡水 053000)(2018年4月11日收到;2018年4月21日收到修改稿)
1 引 言
近年来随着航空技术的高速发展以及太赫兹技术的应用,对高速飞行器再入式通信“黑障”现象的研究已经成为一项重要的课题.飞行器在空间高速飞行过程中与表面气体摩擦,形成包裹在表面的一层高温等离子体,高温等离子体的存在阻断了飞行器与外界的通信交流,这种通信障碍现象称之为“黑障”.由于等离子体对电磁波具有高通滤波特性,目前有学者研究采用太赫兹通信技术解决“黑障问题”[1−7].陈春梅等[8]研究了太赫兹波入射磁化等离子体的传输与衰减问题,讨论了磁场及入射角度对等离子体平板反射、透射系数的影响,但主要以冷等离子为计算模型,没有考虑等离子体高温特性的影响.袁承勋等[9,10]研究了热等离子体太赫兹波的吸收特性,对太赫兹波的反射与透射问题没有详细的讨论.电子科技大学伍习光等[11]采用时域有限差分法(FDTD)研究了等离子体平板的传输特性,计算模型以冷等离子体模型为基础,得到了电子密度、碰撞频率等参数对太赫兹波反射、透射系数的影响.刘建晓等[12,13]和杨宏伟等[14]研究了等离子体及各向异性介质的电磁散射问题.关于等离子体的电磁特性研究涉及电磁传播、散射、吸收等各个方面,但大部分停留在对冷等离子体模型的分析,对高温等离子体,特别是强磁影响下的各向异性高温等离子体的研究较少[15−19].本文以高温等离子体模型为研究对象,分析了磁场、电子温度等参数对太赫兹波透射现象的影响.研究发现,高温等离子体对右旋极化太赫兹波具有高通滤波特性,但在低频太赫兹波段,适当选取外界磁场与温度,阻带中会产生一尖锐的透射峰,并且该透射峰可调节,其频率受磁场影响,峰值的幅度受温度影响.
2 物理模型
本文采用垂直极化波垂直入射到高温等离子体平板中,入射面为xOz平面,模型为三层结构,高温等离子体平板在中间,两侧为真空.考虑到计算精度与计算的通用性,将等离子体所在空间分成N个亚层,模型如图1所示.设每一层的入射角为θi(i=1,2,3,···),折射角为φi(i=1,2,3,···),则1,2两层间的反射系数和透射系数可以表示为[20]:
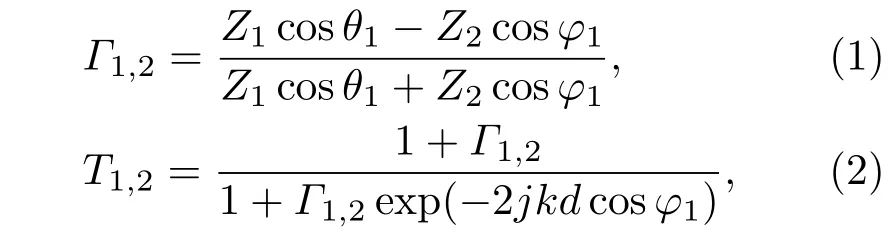
其中Zi(i=1,2,3···)为每一层的电磁波波阻抗,k为每层中的电磁波传播常数,d为每层介质的厚度.介质层2,3处的反射系数为

其中Zeff为2,3界面处的等效波阻抗,计算公式为

则等离子体平板总的反射系数可以按以上方法递推求出.总透射系数可表示为

对于多层介质的计算方法,以此类推,这里不再赘述.本文考虑电磁波垂直入射高温等离子体,因此θi=φi=0,高温等离子体介电常数可以表示为[21,22]

其中T为电子温度,me为电子质量,kB为玻尔兹曼常数,c为真空中的光速,ωp为等离子体角频率,ve为碰撞频率,ωb为电子进动角频率,一般与外加磁感应强度B成正比.
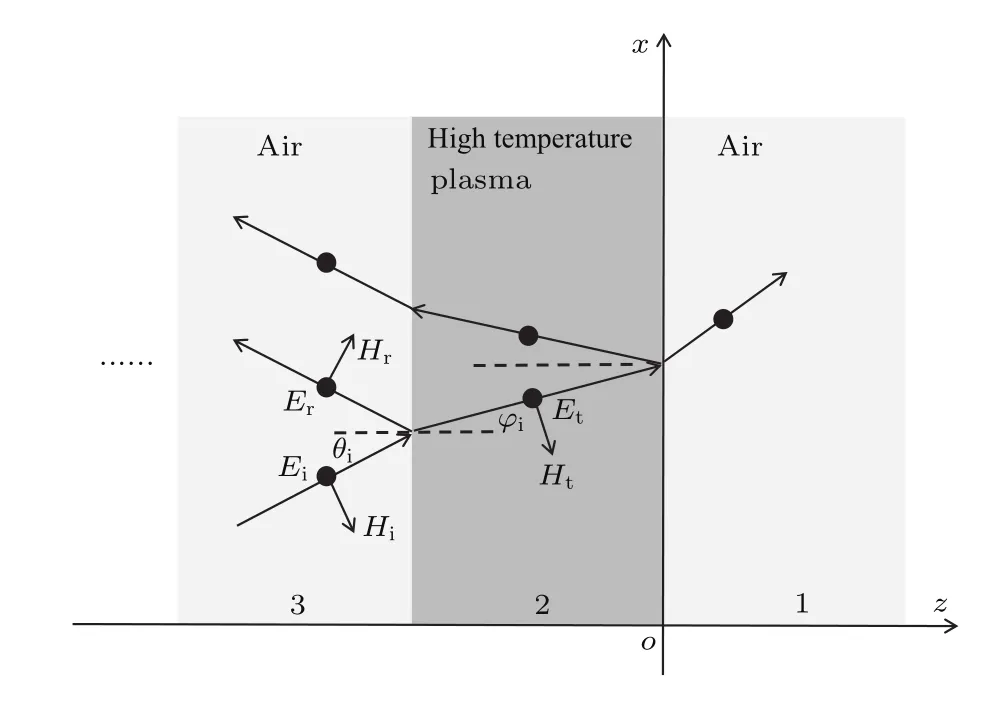
图1 计算模型Fig.1.Schematic diagram of calculation model.
3 算 例
本文主要以右旋极化波为研究对象,讨论温度T与磁场B对高温等离子体传播特性的影响,其他参数如等离子密度、碰撞频率等暂作为定值.当考虑右旋极化波时,(6)式中ωb前的符号取负值.高温等离子体平板厚度取d=0.01 m,磁感应强度B=3 T,电子密度ne=1020/m3,碰撞频率ve=0.5×1012rad/s.图2为电子温度T取不同值时等离子体平板的透射率.可以看出,当温度为100 keV以下时,在0—0.3 THz的低频范围内透射率几乎为0,即基本没有电磁波穿透高温等离子体.而当温度升高到200 keV时,在0.1 THz频点附近出现了一个微弱的透射信号.当温度升高到250 keV时,透射信号的峰值达到了0.27.当温度取268 keV时,透射峰值接近于0.9,几乎对该频率的电磁波完全透射.而在温度升高过程中发现透射峰的频率基本没有发生变化,仅透射峰的幅度在增加.随着温度的升高阻带的频带范围也逐渐展宽,由0—0.2 THz变化至0—0.3 THz.
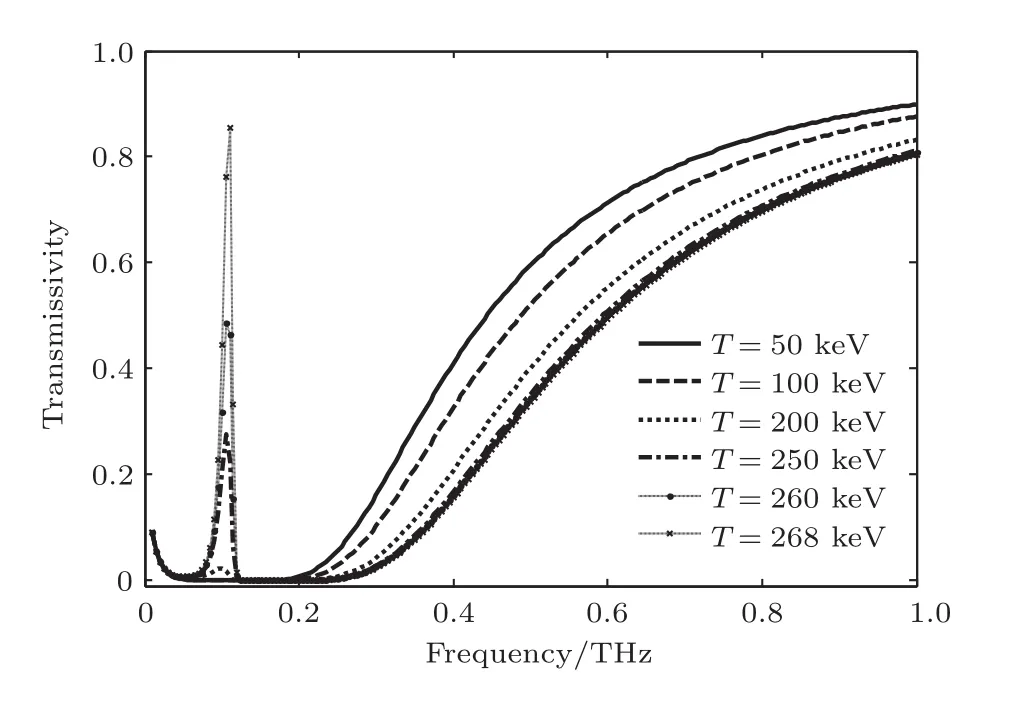
图2 电子温度变化时等离子体平板的透射率Fig.2.Transmissivity of a plasma slab at different electron temperatures.
图3为电子温度取100 keV时,磁感应强度B对透射率的影响.当B=0时,阻带中心在0.1 THz,且阻带内没有透射信号产生.当B=1,3 T时,阻带整体及其中心频率向高频方向移动,但阻带中没有透射峰产生.当B=5 T时,在阻带中的0.15 THz处产生了微弱的透射信号.随着B的继续加,透射峰越来越明显.并且可以看到峰值频率也向高频段发生偏移.当B=5.9 T时透射峰值达到了0.8左右.
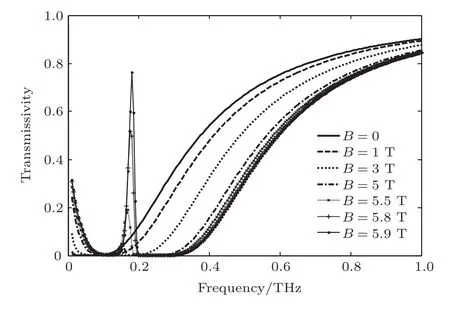
图3 磁感应强度变化时等离子体平板的透射率Fig.3.Transmissivity of a plasma slab at different magnetic field B.
比较图2和图3中电子温度和磁感应强度对透射峰的频率及峰值的影响,发现透射峰的频率主要与B有关,而幅值的大小主要与T相关.因此,可以改变B的值以产生不同频率的透射峰,同时在该频率处调整T的值即可使透射峰的幅值达到1.0附近.这样,对于高温等离子体平板可以通过调整这两个参数来产生不同频率的透过率峰值.表1为参数B,T与透过率峰值频率f的对应关系.图4为根据表1的部分结果绘制的透过率峰值图.可以看出,不同的B值对应了不同的透过频率,随着B的升高,透过频率也相应升高.透过率峰值对应的B值越大,其所对应的温度则越低.

表1 计算得到的透过率在1附近时,峰值频率f与所对应的B,T关系Table 1.Relationship between peak frequency,magnetic field B and electron temperature T at the transmittance of about 1.
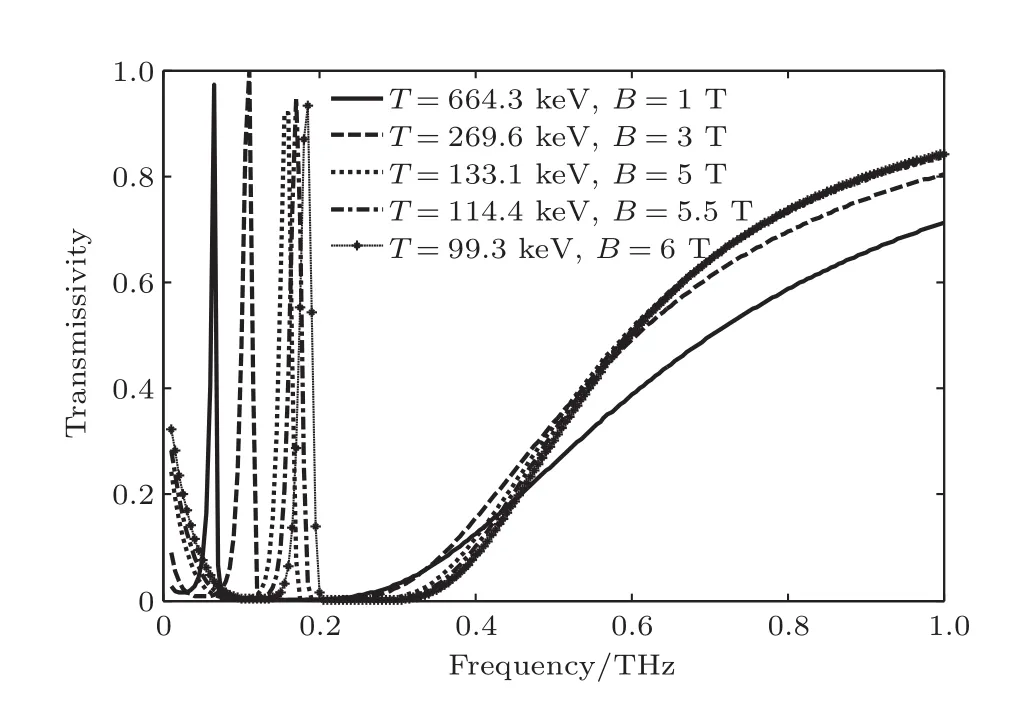
图4 高透射率频率与磁场的对应关系Fig.4.Relationship between high transmission frequency and magnetic field.
根据表1的计算结果绘制f-B曲线与T-B曲线,如图5和图6所示.由图5可知,在透过率接近1时,其峰值频率f与磁感应强度之间为线性关系,通过数据拟合得到曲线方程为

由图6可知,T-B曲线呈指数函数关系,经指数拟合得
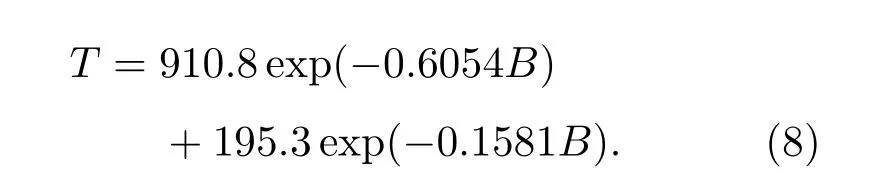
利用拟合得到的(7)式和(8)式,可以求出电磁波垂直穿过高温等离子体平板时产生任意频率透射峰的磁场B与电子温度T.

图5 透过率峰值频率所对应的f-B曲线Fig.5.f-B curves corresponding to the peak transmission frequency.
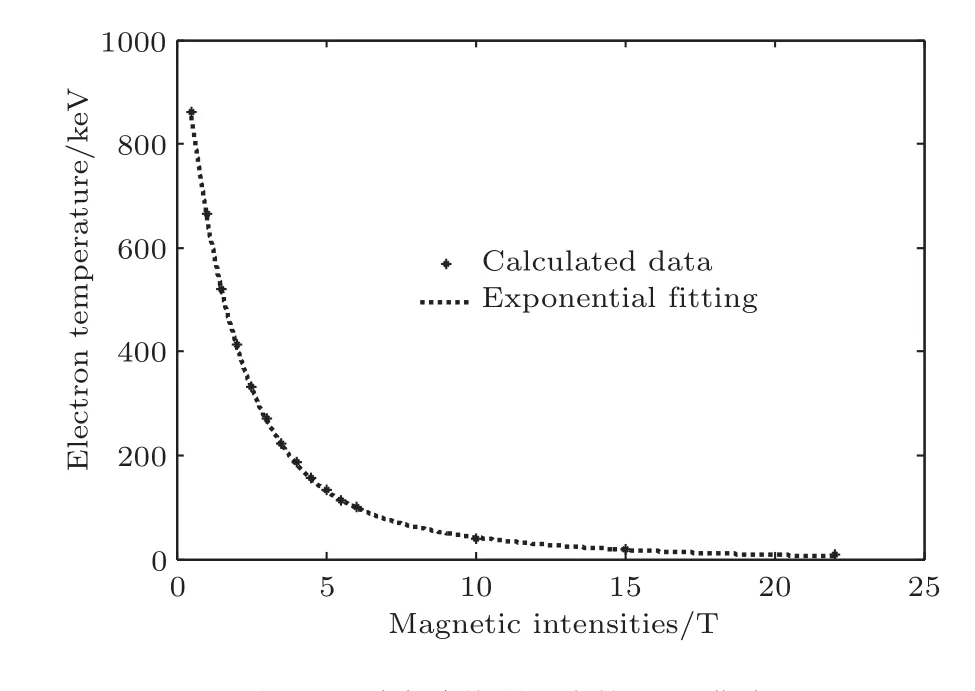
图6 透过率峰值所对应的T-B曲线Fig.6.T-B curve corresponding to the peak transmission frequency.
采用以上拟合方程即可求得在任意频率下产生高透过率的条件.对上述结论,通过FDTD方法对表1中部分数据进行仿真计算,结果如图7所示.入射波源为微分高斯脉冲,迭代方程为
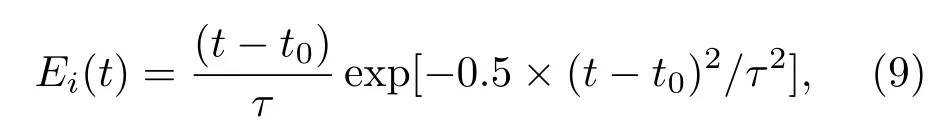
其中τ=25,t0=35τ,计算网格取dx=5µm,dt=dx/(2c),计算空间为2200网格,等离子体占2000网格,计算执行20000时间步.图7中计算了B=3,6,10 T时所对应的透过率峰值分布.由计算结果可知,B=3 T时FDTD计算的峰值频率为0.105 THz,表1中为0.109 THz;B=6 T时FDTD计算的峰值频率为0.184 THz,表1中为0.183 THz;B=10 T时FDTD计算的峰值频率为0.289 THz,表1中为0.290 THz.比较发现两种方法计算结果基本一致,从而证明了该研究的正确性.
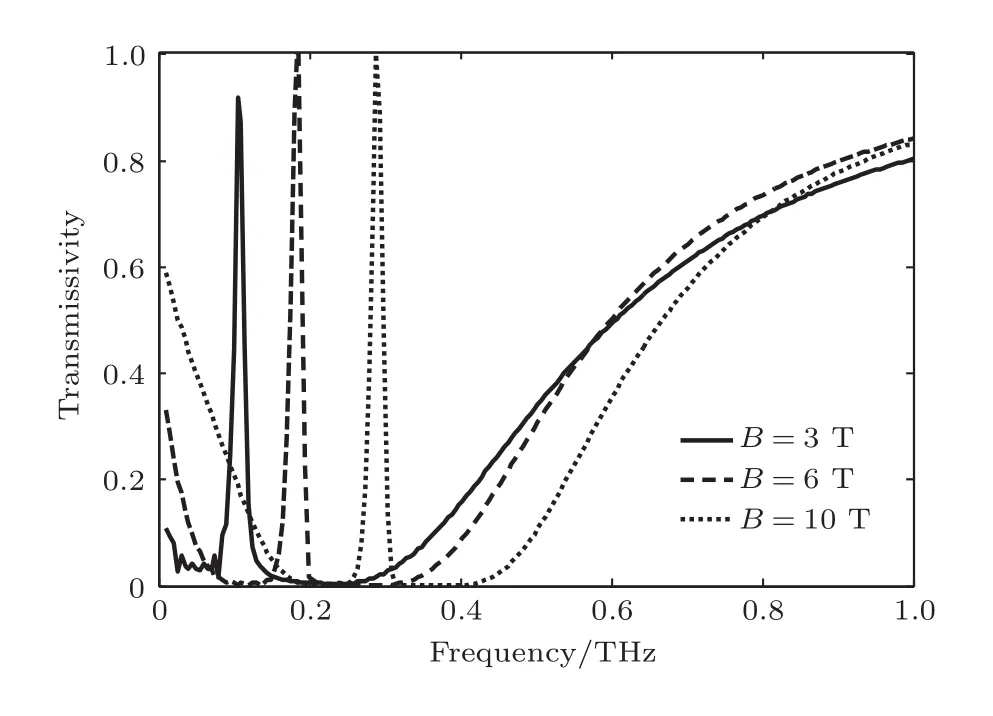
图7 采用FDTD方法根据表1数据计算的透过率Fig.7.Transmissivity calculated by FDTD method according to table 1.
4 结 论
通过数值方法研究了高温等离子体中的阻带透射峰现象.对透射峰产生的条件进行了分析,得到了透射峰频率的计算公式及参数设置的方法.通过FDTD方法进行了验证,结果与本文分析结果基本一致,验证了本文分析的正确性.由于采用计算结果拟合函数时没有考虑等离子体密度、碰撞频率及等离子体平板厚度等因素的影响.因此,所拟合的参数是否具有通用性还有待进一步验证.并且各拟合参数的物理意义还并不明确,这些问题都还需要进行大量的研究.

