数值模拟抽运分布对端泵激光器晶体热透镜球差的影响∗

姚强强 王启晗 冯池 陈思 金光勇 董渊

(长春理工大学理学院,长春 130022)(2018年1月16日收到;2018年6月2日收到修改稿)

1 引 言

自从研究发现热透镜球差对固体激光器的输出光束质量具有严重的影响以来,对晶体热球差的研究就从未停止[1−5].为了减少甚至避免球差的产生,科研人员对球差进行了大量的研究,例如抽运功率、吸收系数对球差的影响等[6−10].但仍然有一些不足之处,目前对激光晶体内部热分析时,常常假设其抽运光为均匀分布或者高斯分布[11−13].这些假设给激光晶体的热分布模型带来较大的误差,因而影响到光程差(OPD)、球差,甚至光束质量的仿真分析.然而很少有人从抽运光分布对热透镜球差的影响方面进行研究.

本文通过对不同分布的抽运光抽运Nd:YVO4晶体时的工作特点进行分析,建立了具有通用性的热透镜球差分析模型.在用解析法对各向异性晶体的热传导方程进行求解的基础上,分析抽运光的分布对晶体温度分布的影响,从温度分布求解出相位差的分布,进而通过Zernike多项式的展开,分析热透镜球差的变化,建立起抽运光分布系数与球差的一般表达式.研究仿真了各向异性矩形截面Nd:YVO4晶体在受到不同分布抽运光抽运时,晶体内部产生的温度场分布和球差变化,对抽运功率在其中的影响进行了分析,并对二阶超高斯光抽运球差最大的现象进行了理论分析.研究方法和结果具有普遍适用性,对不同实验环境下的激光器端面抽运激光晶体热透镜球差计算具有理论指导作用;对从改变抽运光分布的角度改善球差、提高激光器输出特性提供了理论依据.

2 理论分析

以半导体激光器(LD)作为抽运源的全固态激光器(DPL),因其具有独特的优势及广阔的应用前景,逐渐成为固体激光器的一个重要发展方向.对其抽运源的工作原理进行深入分析可知[14],为了改善入射到晶体上激光强度的均匀性,抽运源内二极管出射光束是经微透镜聚焦后进入光纤,再将光纤捆扎成束,从尾端出射,则其光强分布应用超高斯函数来表示[15−17],在激光晶体内不同位置处的光强度分布表达式为

式中ω为光束的高斯半径;β为吸收系数;a,b为x,y方向的尺寸;k为不同抽运分布的系数,当k=1时为高斯分布,当k≥2时为超高斯分布,其中k较大时为平顶光束,当k=∞时,其光强分布在束腰半径范围内可视为均匀分布.不同阶次光强的分布情况如图1所示.

式中PP为单端抽运时的抽运功率.

晶体内的温度分布可以通过求解稳态热传导方程获得:

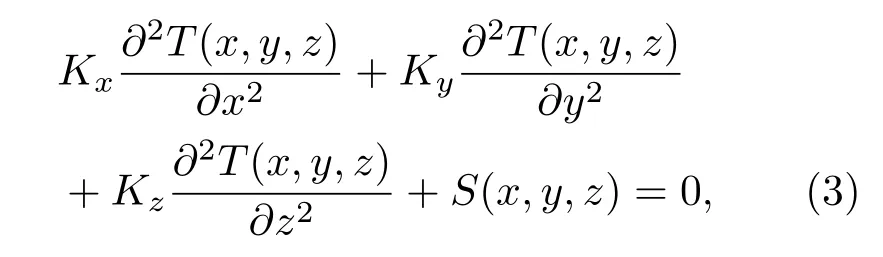
式中T(x,y,z)为晶体的温度分布;Kx,y,z为热传导系数;S(x,y,z)为热源函数.

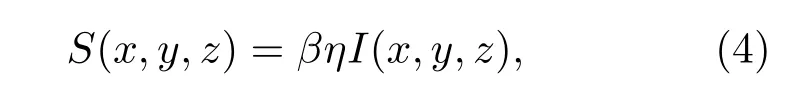
式中β为激光晶体对抽运光的吸收系数;η为由荧光量子效应和内损耗决定的热转换系数;η=1−λp/λl,其中λp为抽运光波长808 nm,λl为振荡光波长1064 nm.通过对(3)式进行求解,得到晶体内部的温度分布[18].

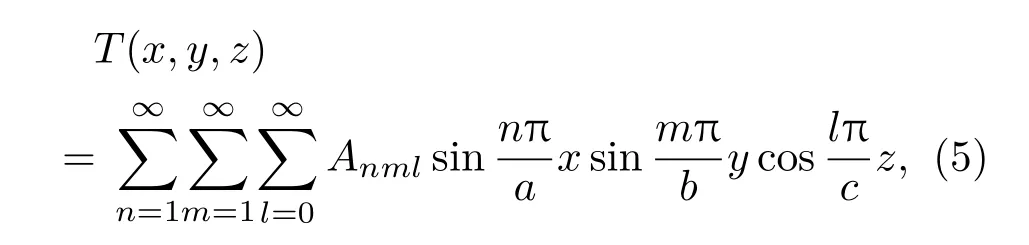
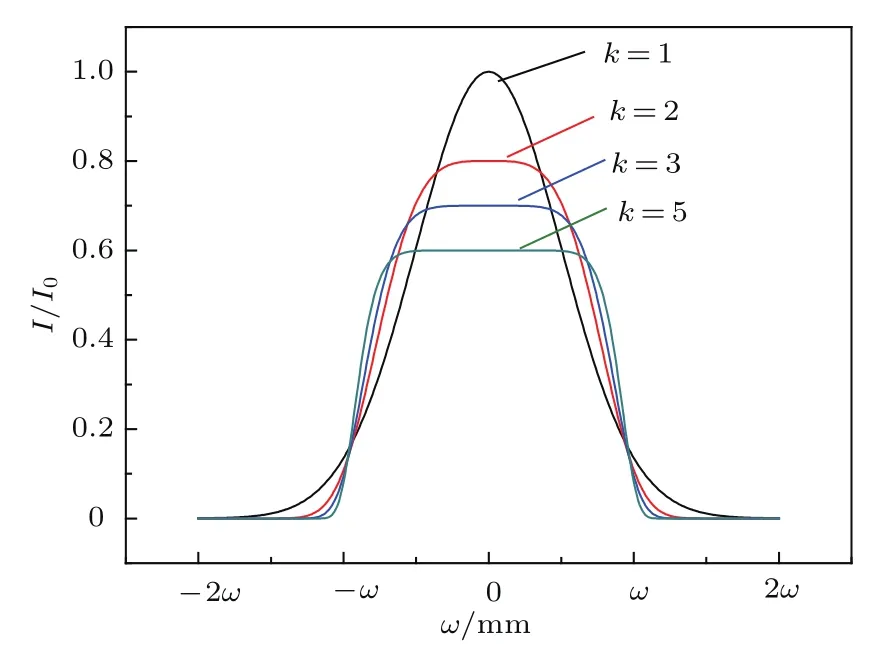
图1 不同阶次的超高斯分布对比图Fig.1.Contrast diagram of super-Gauss distribution diagram of different orders.

这种温度的分布并非是均匀分布,而是梯度式的分布,这种梯度式的温度分布会导致折射率梯度分布和热形变,严重影响激光器的品质,晶体内的温度差可表示为

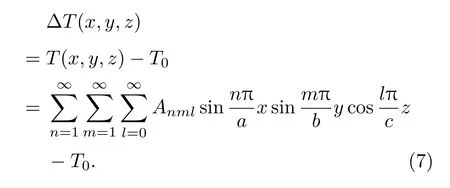
同时折射率梯度分布和热形变导致在晶体内传播附加的相位不一样,引入OPD,其微分形式为

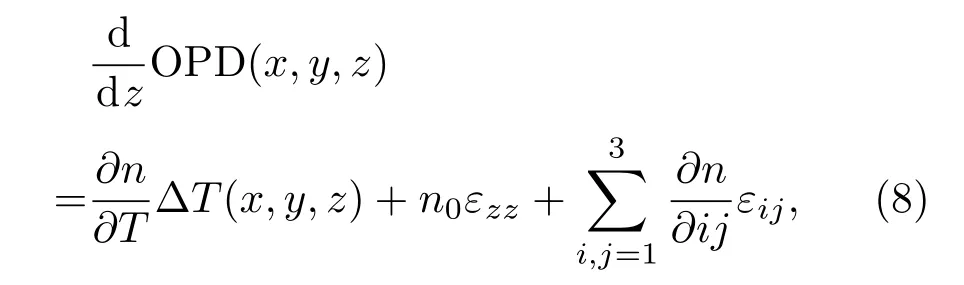
式中εzz=(1+µ)αTΔT(x,y,z)为纵向应变;µ为泊松比;αT为热膨胀系数;n0为室温下晶体的折射率.(8)式右侧第一项为折射率随温度变化产生的折射率梯度变化,第二项为纵向应变引起的晶体端面形变,第三项为热致双折射.对Nd:YVO4晶体来讲,相比第一项和第二项,第三项热致双折射产生的相位差要小得多(计算和仿真结果表明热致双折射产生的相位差约占总相位差的3%—6%之间),可以忽略不计.因此对(8)式积分,可得到OPD为

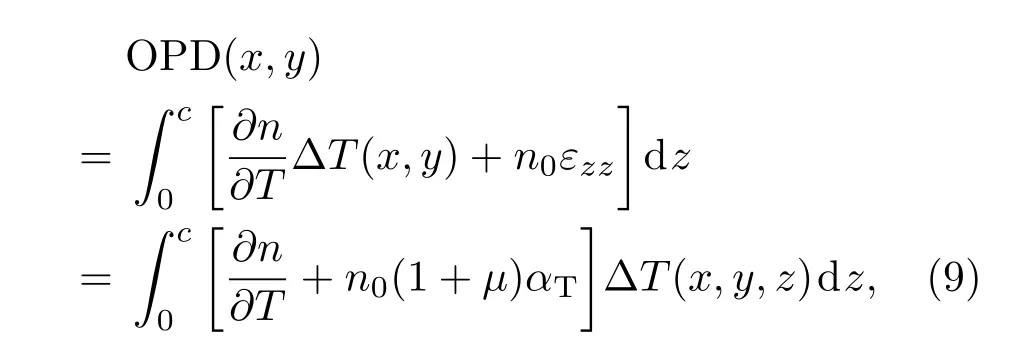
其中∂n/∂T为热光系数;c为晶体长度;λx,λy分别为x,y方向的热导率.

对应的附加相位差Φ(x,y)为

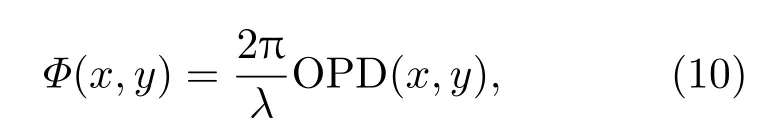
其中λ为波长.

联立(9)式与(10)式可得:

由于Zernike多项式具有正交和圆对称性,这和光斑的性质非常符合,适合用来表示光学畸变,常被用来表征光学的畸变量,故将相位差分布用Zernike多项式展开如下:

式中N为Zernike多项式的总阶数;Zn(x,y)为n阶Zernike多项式;cn是其系数.通过文献[19,20]可知,在Zernike多项式中第13项Z13=1−6y2−6x2+6y4+12x2y2+6x4表示光束中的球差项,对应的c13是相应的Zernike球差系数[21].结合前面的(6),(7)和(11)式,通过广义逆矩阵法[22]对(12)式中的系数cn进行求解,便建立起不同抽运分布系数k和球差系数c13的关系式,如下所示:

3 数值仿真与分析

仿真采用的是单端抽运Nd:YVO4晶体,晶体尺寸为3 mm×3 mm×10 mm,抽运光波长为808 nm,晶体抽运光束束腰半径为300µm,吸收系数2.6 cm−1,热光系数∂n/∂T为8.5×10−6K−1,晶体传热系数为6.5 W·m−2·K−1,热膨胀系数4.43×10−6K−1.首先在抽运分布系数k=1(抽运光强分布为高斯分布)时,仿真了不同抽运功率下晶体x-y平面的温度分布,如图2所示.可以看出随着抽运功率的增加,晶体内的温度逐渐升高,且分布均匀度变差.

图2 在k=1,Pp=40 W时晶体内x-y平面y(x)轴向温度分布图Fig.2.Temperature distribution diagram along the y(x)axis with k=1,Pp=40 W in the x-y plane.

在此基础上对抽运分布系数k取1,2,4,10,100和∞时的晶体温度分布进行了计算,以抽运功率40 W为例进行仿真,仿真结果如图3所示.可以得出在相同抽运功率的情况下,超高斯分布阶数k取2时晶体温度最高,除高斯分布(阶数为1)外,抽运分布系数k越大,晶体的最高温度反而越低;由于Nd:YVO4晶体热导率较大,吸收率较高,对于单端LD抽运的激光器而言,前部中心温度比后部高,且不同分布情况时温度差异主要集中在晶体前部和中部,后部无明显差异.

图3 抽运分布系数k对晶体温度的影响Fig.3.Effect of the pump distribution coefficient k on the temperature of crystal.

在相同的计算仿真条件下,取抽运光分布系数k分别为1,2,4,10,100和∞时,计算了晶体产生的OPD,仿真结果如图4所示.可以得到在相同抽运功率时,晶体产生的最大OPD分别为3.00λ,3.05λ,2.99λ,2.93λ,2.87λ,2.86λ. 从图4中可知,不同的抽运光分布产生了不同的OPD,且抽运光分布对OPD的分布存在明显的影响;超高斯分布阶数为2时,产生的OPD最大,除高斯分布(k=1)外,随着抽运分布系数的增加,OPD逐渐减小.

利用(13)式,对抽运光分布阶数k分别取1,2,3,4,6,8,10,20,50,100和∞时的球差系数进行了计算,仿真结果如图5所示.由图5可知:超高斯分布阶数k取2的球差最大;除高斯分布(k=1)外,随着k的增大球差系数逐渐减小,当k趋向无穷时,k对球差的影响趋于稳定.

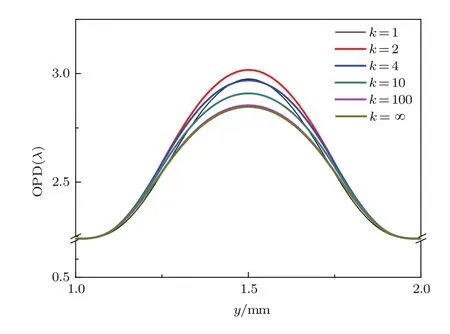
图4 OPD随抽运分布系数k的变化曲线Fig.4.Variation curve of OPD with pump distribution coefficient k.

对不同抽运功率下的球差系数进行了计算,仿真结果如图6所示.通过对图5和图6的分析可知:在相同的抽运功率下,抽运分布系数k对球差的影响符合相同的规律;在相同抽运分布的情况下,随着抽运功率的增加,球差逐渐增大,且随着抽运功率的增加,抽运分布系数k对球差的影响作用加重,即在抽运分布系数k不同时,球差的变化逐渐增大.

对于抽运分布阶数k=2球差最大这种现象进行进一步分析,由(1)式可知,平行z轴入射到晶体表面的超高斯光强分布表达式为

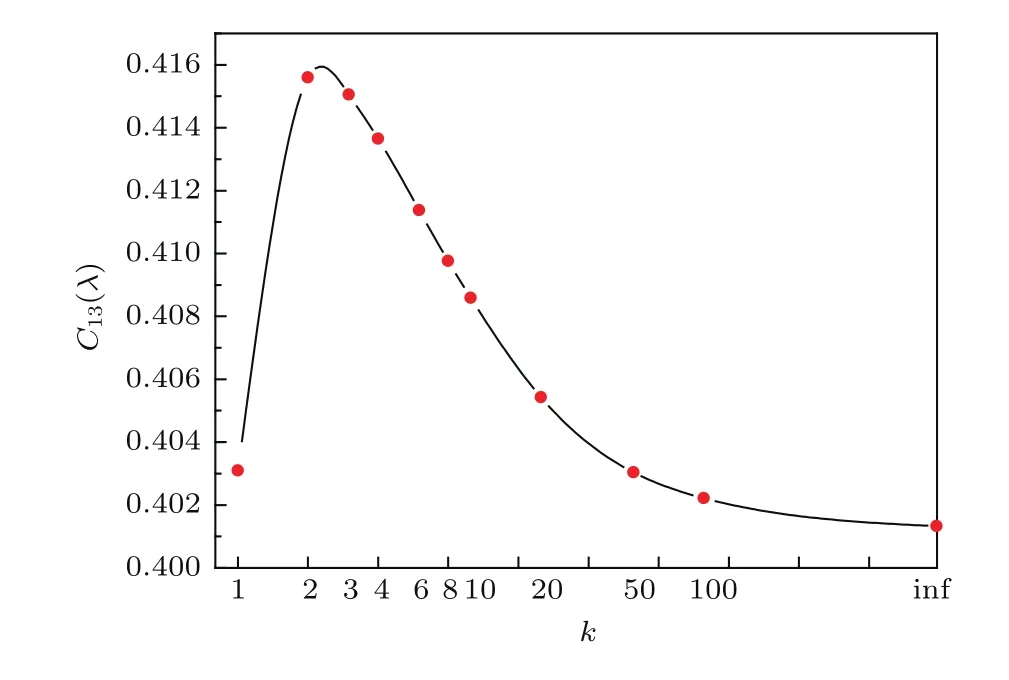
图5 球差系数随k的变化曲线Fig.5.Variation curve of coefficient of spherical aberration with the change of k.

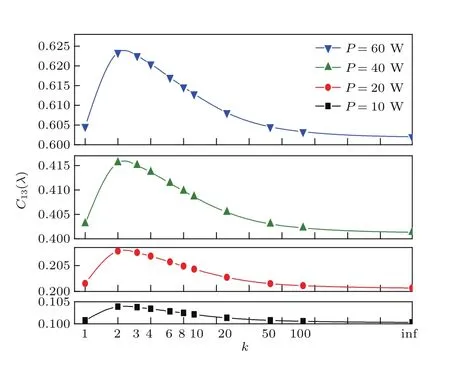
图6 随着抽运功率的增加,球差系数随k的变化Fig.6.With increase of pump power,variation of spherical aberration coefficient with k.

考虑到抽运源的光强分布具有圆对称性,同时为了便于后续研究的直观性,对模型进行极坐标转换并且将坐标圆点移动到晶体端面中心位置.(14)式可表示为

其中r满足下式

其中θ为极坐标下的极角.

抽运到晶体端面的激光功率为

则抽运到端面特定区域内的激光功率为

其中t为特定区域半径.

结合(2)式可将(18)式整理为

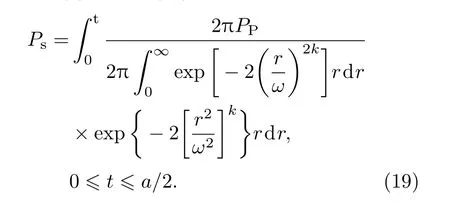
建立晶体端面抽运光功率分布模型,仿真条件跟前文相同,对(19)式进行求解,发现t取值不同(即特定区域大小不同)时,抽运分布阶数k对激光功率Ps的影响不同,图7列举了部分t时不同阶次k下Ps在Pm比重的变化.

图7中γ表示在特定区域内不同抽运分布系数k下激光功率占总功率的比重,可以发现随着t的增加,不同阶次的超高斯光束所占的比重都在增加,这是由所计算特定区域t的增加引起的,但同时抽运分布系数越高的项所占的比例逐渐增大,这就说明阶数越高的光束作用最强的区域越靠外侧.对不同抽运分布系数k下激光功率所占比重最大的区域t的范围进行求解,结果如图8所示.

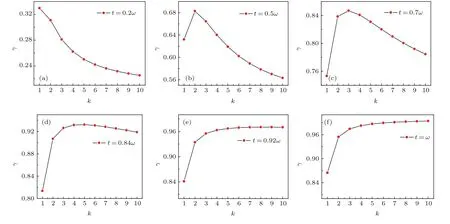
图7 不同t时,抽运分布系数k对功率Ps在Pm中所占的比重的影响 (a)k=1;(b)k=2;(c)k=3;(d)k=5;(e)k=8;(f)k=10Fig.7.Proportion of pump distribution coefficient k in power Ps/Pmwhen t is different:(a)k=1;(b)k=2;(c)k=3;(d)k=5;(e)k=8;(f)k=10.

从图8可以看出,相比1阶高斯分布光束的范围0—0.3ω,二阶超高斯分布光束激光功率最强的范围(红色区域)0.30ω—0.63ω更宽,示意图如图9所示.也就是说当二阶超高斯光束照射在晶体端面时,能得到最强激光功率的照射面积最大,从而相比其他阶次超高斯光束,二阶超高斯光束引起的热效应更严重,也就解释了二阶超高斯光束热透镜球差最严重的原因.

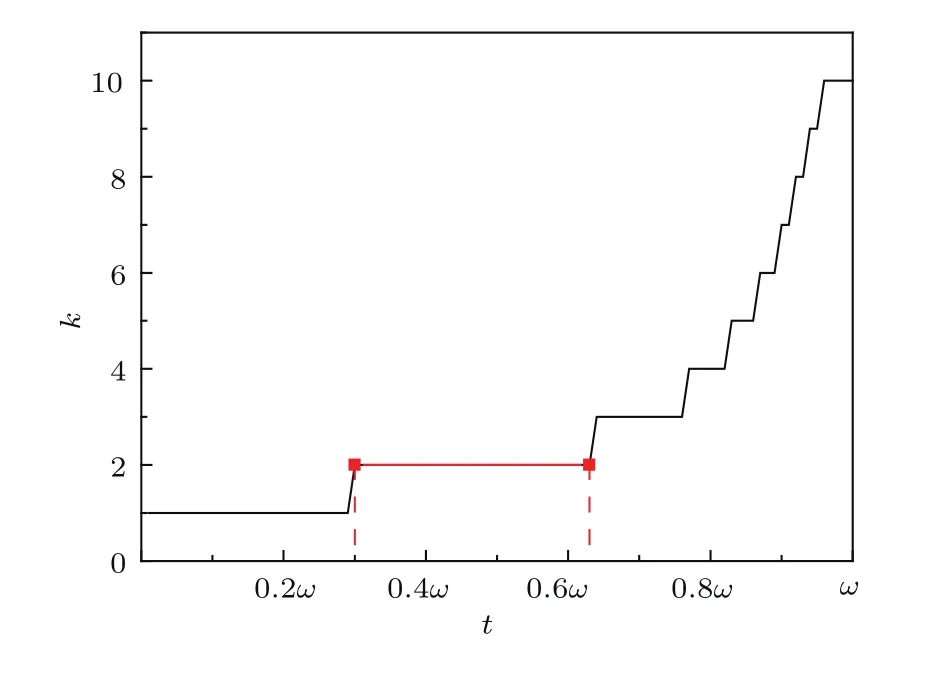
图8 不同区域各阶超高斯光最强的范围Fig.8.Range of strongest super-Gauss in different regions.

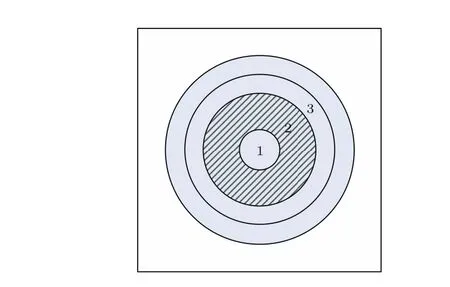
图9 二阶超高斯光功率最强的范围图Fig.9.Strongest range diagram of 2 order super-Gauss light power.

4 结 论

本文通过分析Nd:YOV4晶体的工作特性,建立了一个单端抽运,四周恒温的热模型.从各向异性的热传导方程出发,求解了晶体内部的温度分布、相位差分布,最后通过广义逆矩阵求解出Zernike多项式系数,建立起抽运光分布系数k与球差系数的关系表达式;定量地分析了两者的关系,及抽运功率对两者关系的影响;同时对仿真结果进行了理论分析,解释了二阶超高斯分布球差最大的原因.本文的研究方法和所得结论具有普遍的适用性,可用于其他激光晶体温度分布、热形变、OPD分布、球差分布的定量分析;同时也为从改变抽运光分布的角度改善球差、提高激光器输出特性提供了理论参考.