一种面向海量数据的spilt-and-conquer方法

温 焜，兰晓然

（1.南昌大学 管理学院，南昌 330029；2.江西行政学院，南昌 330003；3.中国人民银行沧州市中心支行，河北 沧州 061000）

0 引言

变量选择[1，2]在对维数过大样本量过多的的数据集进行降维的时候，通常会遇到两个问题：计算开销太大和欠学习。就目前而言大多特征选择算法的时间复杂度是样本数的二次甚至更高次，同时与维数成正比，导致在对高维海量数据集进行变量选择时消耗的时间就会过长；在面对样本数远远大于特征维数的高维小样本数据集时，进行特征选择就容易出现欠学习问题。因此如何有效的对高维海量数据集进行变量选择，是变量选择研究要迫切解决的问题。

在进行变量选择时可以选择Lasso[3]，LARS算法[4]SCAD估计方法[5]和MCP估计算法[6]等，本文选择了Lasso方法进行变量选择[3]。这种算法通过构造一个惩罚函数获得一个精炼的模型，通过最终确定一些指标的系数为零，LASSO算法实现了指标集合精简的目的。这是一种处理具有复共线性数据的有偏估计[7]。

1 Lasso方法

LARS算法，SCAD估计方法和MCP估计算法都可以用来进行变量选择，而Lasso算法在某些方面具有一定的优越性，所以本文采用Lasso方法进行研究。Lasso方法是很常用的一种变量选择的方法，是1996年Tibshirani提出的。它既能对变量进行选择,又能得出参数估计值的一种方法，而且选择出的变量具有很好的解释性。

考虑如下普通线性方程：

其中 Y=(y1，y2，…,yn)T为响应变量，n 为样本容量，X=(X1，X2，…，Xn) 为 p 维 预 测 变 量 ，假 设 观 测 数 据(yi，xij)，i=1，2，…，n ，j=1，2，…，p 已经过中心标准化处理，即：

除特别说明外，在下文出现的数据（X,Y）均为经过中心标准化处理的。

设对固定非负数，Lasso方法定义如下:

R统计软件的Lars算法的软件包提供了Lasso算法。根据模型改进的需要，数据挖掘工作者可以借助于Lasso算法，利用AIC准则和BIC准则精炼简化统计模型的变量集合，达到降维的目的，因此，Lasso算法是可以应用到数据挖掘中的实用算法。

2 spilt-and-conquer方法

spilt-and-conquer方法[8]，经过变量选择在组合选择后，它不仅能够很好的去除错误模型选择带来的伪相关，而且可以极大地降低计算时间。变量选择的时间复杂度一致于O(napb)，a＞1，b≥0 。

对应的惩罚估计为:

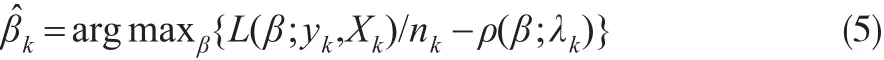
其中 ρ(β;λk)训练参数 λk的惩罚函数，可参见Fan和Lv（2011）。

本文考虑 p是有限的，β是非稀疏的，假设XTX是可逆的，那么使用全数据进行最小二乘估计为，这里把数据集分成K份。

假设XkTXk是可逆的，那么从kth份得到的最小二乘估计为：

公式(7)中Xk是正交矩阵，yk是数据集kth份的响应向量，由K个部分可以结合成一个新的估计，如下：

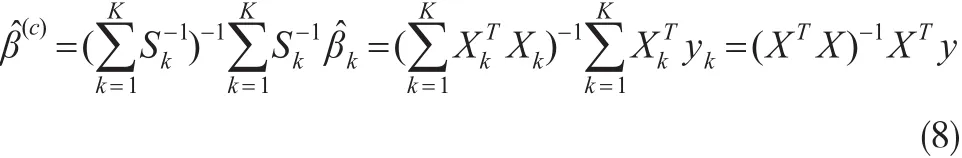
3 实验分析

3.1 实验数据

为了检验spilt-and-conquer方法在高维海量或高维小样本数据集表现的优越性，本文选择了三个高维数据集，三个低维数据集。本文数据集来自UCI数据库、17年数学建模、R库，为了便于比较本文抽取了部分数据。数据库具体描述如表1所示。

表1 实验数据集描述

针对以上数据集，首先将分而治之的Lasso方法用在三个低维的数据集上，并与传统的Lasso方法进行对比，表明其并没有降低分类精度。然后在高维的数据上将改进的Lasso方法与传统Lasso方法进行对比，发现spilt-and-conquer方法不仅在预测精度上不受影响，对一些数据集还会提高其预测精度。实验表明，spilt-and-conquer方法能够有效解决高维数据中遇到的过学习和计算时间过长、计算消耗过大的问题。本文选择SVM、随机森林、神经网络做分类器，并采用5倍交叉验证的方式进行实验。

3.2 实验过程

（1）使用SVM、随机森林、神经网络做分类器，将三种预测结果求平均值。在R语言加载包，以实现这三种分类器。

（2）调整参数lambda的确定：对lambda的格点值，进行10折交叉验证，选取交叉验证均方误差误差最小的lambda值。然后，按照得到的lambda值，用全部数据重新拟合模型。

（3）对三个低维的数据集进行特征选择，设K为2、3、4以均分的原则进行划分，分别用Lasso方法spilt-and-conquer方法进行变量选择，并使用三种分类器进行预测，比较预测精度。

（4）对高维的数据集进行变量选择，设K分别为1、2、4、6，然后分别用两种方法进行变量选择并比较预测精度。

3.3 实验结果

3.3.1 在低维数据集上的实验比较

对三个低维数据集分别用Lasso和spilt-and-conquer方法进行处理，将结果运行100次取平均值，结果如表2所示。

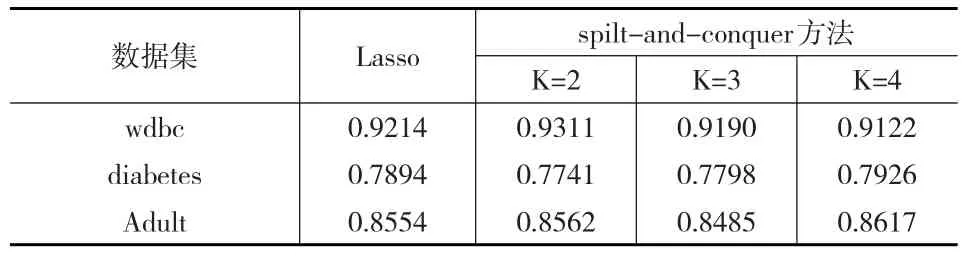
表2 低维数据集预测精度对比表

通过表中的结果，可以得出spilt-and-conquer算法与传统的Lasso算法相比，精度相差不大。在wdbc和Adult数据集中，分别当K=2、K=4时预测结果还相对较好。由于数据量比较小，计算时间相差不大。基本在一分钟之内可以计算出结果。

3.3.2 在高维数据集上的实验比较

对三个高维海量数据集分别用Lasso和spilt-and-conquer方法进行处理，将结果运行100次取平均值，为了方便比较本文对数据集的维数和样本数进行了选取。结果如表3所示。

表3 高维数据集预测精度对比表

在表3中，K=1意味用全数据集进行Lasso估计，为了比较本文使用了K=2、4、6。Lasso算法试图保留更多相关变量。由表3列出的计算时间和预测精度可以看出，spilt-and-conquer方法不仅提高了预测精度，而且很大程度的节省了计算时间，减少了电脑消耗。原理上来说，spilt-and-conquer方法进行分块，删除了冗余变量，结合后再次进行变量选择，只留下对结果影响较大的变量，使预测结果有一定提高。将变量分开，就相当于用计算机并行计算，可以有效缩短计算机运行时间。

3.3.3 在高维数据集上的运行时间比较

固定数据集的维数，记录三个数据集与测试运行时间如图1所示。

图1 计算机运行时间对比图

由图1可知，当维数固定时，样本量越大，计算机运行时间越长。所以随着分块个数增加计算机耗费时间减短，且样本个数越多，时间减少的越快。

spilt-and-conquer方法，将数据集进行分块处理，并行运算，很大程度上缩短的运行时间。通过多次变量选择排除冗余变量，也提高的预测精度。所以spilt-and-conquer方法能很好的适用于高维海量数据集。

3.3.4 在低高维数据集上的预测精度比较

将三种预测算法对每个数据集预测效果取平均得到预测结果，如表4所示。

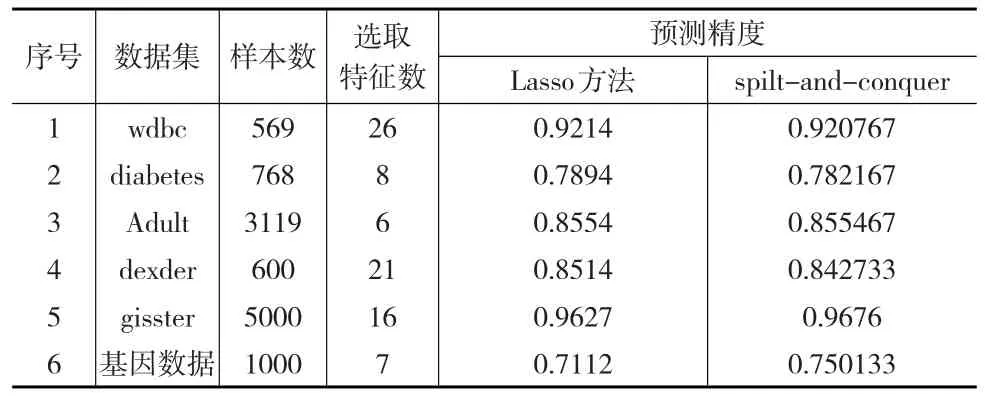
表4 spilt-and-conquer方法和Lasso方法预测精度对比表

由表4可以看出，在低维和高维的海量数据上，除了diabetes和dexder数据集的所有分块的平均预测精度，spilt-and-conquer方法稍低于Lasso方法，其他数据集的预测精度明显更好。综上可以得出spilt-and-conquer方法使用于低高维海量数据集上时，不仅可以很大程度上节省时间，而且可以是预测效果更好。

4 结论

Lasso方法在变量选择时具有好的表现，但是在处理海量的数据集时，会出现费时，计算机消耗过大的问题。于是为了更好地在海量数据集进行选择，本文提出spilt-and-conquer方法，此方法除了具有Lasso的优良性质外，还具有强稳定性，易排除伪相关变量的特性。为了验证spilt-and-conquer方法的优良性质，本文使用SVM、随机森林、神经网络对数据集进行预测并记录运行时间。实验结果表明，spilt-and-conquer方法不仅可以有效的提高预测精度，而且能够很大程度上节省运行时间。说明spilt-and-conquer方法能够很好地适用于高维海量或低维海量数据集。