错题集：学霸的“秘籍”

葛亚美

同学们，错题集是学习过程中必备的学习资料，也是同学们成为学霸的“秘籍”.下面是一元二次方程中容易出错的题目，让我们一起来分析吧！

一、选择题

例1 用配方法解方程x2-6x-4=0，下列配方正确的是（ ）.

A.（x-3）2=5B.（x+3）2=13

C.（x-3）2=13D.（x-3）2=7

【错解】A.

【错因】方程常数项移到等号右边时，没有变号.

【正解】方程x2-6x-4=0变形得：x2-6x=4，配方得：x2-6x+9=13，即（x-3）2=13.故选：C.

【点评】此题考查了解一元二次方程——配方法，熟练掌握完全平方公式是关键.

【正解】由原方程，得根据一元二次方程的定义，知二次项系数a=5，一次

【错解】B.

【错因】把一次项系数-6误认为6.项系数b=-6，常数项故选：C.

【点评】根据一元二次方程的定义来解答：二次项系数是a，一次项系数是b，常数项是c.

例3方程x2=2x的根是（ ）.

A.0 B.2 C.0或2 D.无解

【错解】B.

【错因】两边不能同除以x，因为x可能为0.

【正解】x2=2x

x2-2x=0

x（x-2）=0

所以x1=0，x2=2.故选：C.

【点评】本题考查的是一元二次方程的解法，掌握提公因式法是解题的关键.

例4若（a2+b2-3）2=25，则a2+b2=（ ）.

A.8或-2 B.-2 C.8 D.2或-8

【错解】A.

【错因】忽略了a2+b2是非负数.

【正解】由（a2+b2-3）2=25，得a2+b2-3=±5，所以a2+b2=3±5，解得a2+b2=8或a2+b2=-2（不合题意，舍去）.故选：C.

【点评】本题考查了解一元二次方程中的直接开平方法.要注意a2+b2是非负数.

二、填空题

例5若关于x的一元二次方程（a+1）x2+4x+a2-1=0的一个根是0，则a=______.

【错解】1或-1.

【错因】忽视二次项系数不等于0.

【正解】∵一个根是0，∴（a+1）×（0）2+4×0+a2-1=0，∴a2-1=0，即a=±1；∵a+1≠0，∴a≠-1.∴a=1.

【点评】本题主要考查了方程的根的定义，把求未知系数的问题转化为解方程的问题，是待定系数法的应用，容易出现的错误是忽视二次项系数不等于0这一条件.

例6 关于x的一元二次方程（m-2）xm2-2+2mx-1=0的根是_______.

【错解】

【错因】忽视二次项系数不等于0.

【正解】根据一元二次方程的定义，得解得m=-2.则有方程即故答案为

【点评】要注意一元二次方程的条件：未知数的最高次数是二次，且系数不得为0.

例7已知关于x的方程m（x+a）2+n=0的解是x1=-3，x2=1，则关于x的方程m（x+a-2）2+n=0的解是_______.

【错解】x1=-3，x2=1.

【错因】对整体思想模糊不清.

【正解】∵关于x的方程m（x+a）2+n=0的解是x1=-3，x2=1，∴方程m（x+a-2）2+n=0可变形为m［（x-2）+a］2+n=0，∵此方程中x-2=-3或x-2=1，解得x1=-1或x2=3.故答案为：x1=-1，x2=3.

【点评】此题主要考查了解一元二次方程以及方程的解的定义.解决问题的关键是由两个方程的结构特点进行简便计算.

例8 三角形的两边长分别为3和6，第三边的长是方程x2-6x+8=0的解，则此三角形的周长是_______.

【错解】11或13.

【错因】忽视三角形三边关系.

【正解】x2-6x+8=0，（x-2）（x-4）=0，x1=2，x2=4.当x=2时，2+3＜6，不符合三角形的三边关系定理，所以x=2舍去.当x=4时，符合三角形的三边关系定理，三角形的周长是3+6+4=13，故答案为：13.

【点评】本题考查了三角形的三边关系和解一元二次方程等知识点，关键是确定第三边的大小和分类讨论思想的运用，难度适中.

三、解答题

例9 求一元二次方程ax2+bx+c=0（a≠0）的根（用配方法）.

【错解】ax2+bx+c=0，

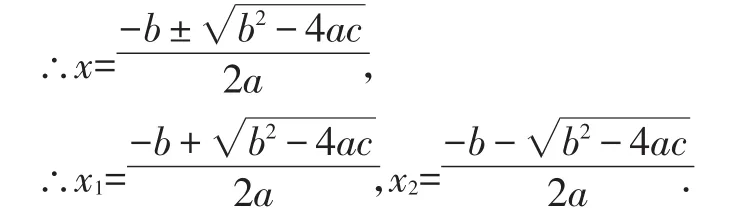
【错因】在开方时对b2-4ac的值是不是非负数没有进行讨论.

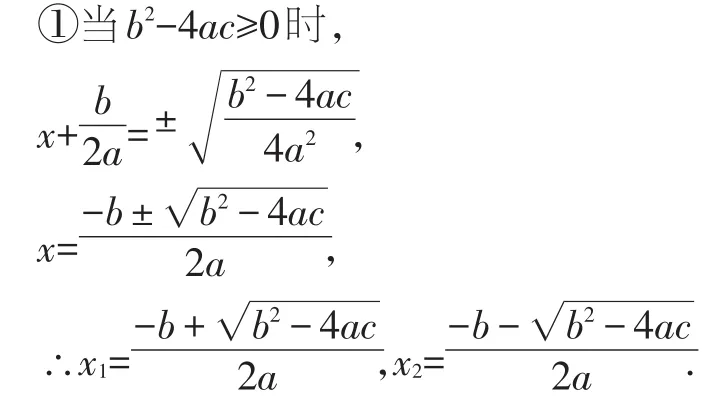
②当b2-4ac＜0时，原方程无解.

【点评】此题属于易错题，同学们往往漏掉对b2-4ac的值是不是非负数进行讨论，所以，在解题时还是多一份细心好.